为实习准备的数据结构（6）-- 优胜树与淘汰树

华为云博客 技术博客 13178 30

在这里插入图片描述

文章目录

前言

大部分人称呼它们为“胜者树”和“败者树”，也有人称呼它们为“优胜树”和“淘汰树”，我觉得还是优胜树和淘汰树比较好听点。

优胜树

优胜树是完全二义树,每个结点的取值足两个孩子的较小值。根据定义,根结点的取值是整个树的最小值。

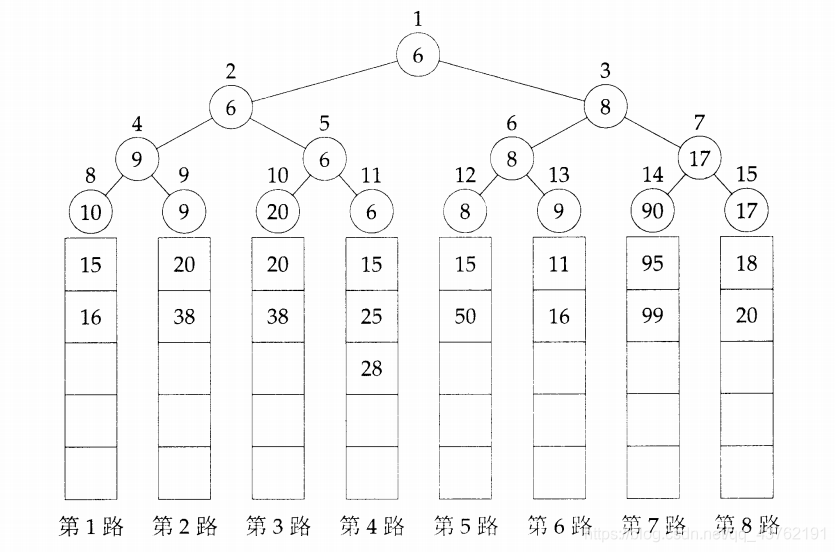
给出八路大军的前三排
这里给出了八路大军的前三排。

如果规定关键字较小的记录获胜,则优胜树与锦标赛的晋级过程相似,每个非叶结点都对应一场比赛的获胜选手,根是赛事的胜者,其关键字最小。由于每个结点通常占用的存储空间较大，为节省空间，在优胜树的归并过程，可用指针指向每路序列的第一个记录，图中的根结点仅包含一个指针,指向第4路的第一个记录。

为什么要这样呢？或者说，看到这里，依然是觉得这棵树平平无奇的。

优胜树的重构

不急，我们来看看优胜树的重构：
以上面的例子为例，取出了第一个“6”之后，第四排及时的补上了一个“15”，
“15”和旁边的“20”进行比较，选出来“15”，
“15”再和旁边的“9”进行比较，选出了“9”，
“9”再和旁边的“8”进行比较，选出了第二个值：8。

从这个演示可以看出这个算法真正吸引我们的地方就是当决出一个胜者后，要取得下一个胜者的比较只限于从根到刚才选出的外结点这一条路径上。可以看出除第一次比较需要n-1次外，此后选出次小，再次小…的比较都是log n次，故其复杂度为O(nlogn)。但是对于有n个待排元素，锦标赛算法需要至少2n-1个结点来存放胜者树。故这是一个拿空间换时间的算法。

优胜树代码实现

typedef struct
{
	int index; int data;
}TreeNode;

TreeNode *buildWinnerTree(int *set, int setsize)
{ int treesize = 2*setsize - 1; TreeNode *tree = malloc(treesize * sizeof(TreeNode)); assert(tree); int i; for(i = 0; i < setsize-1; i++) tree[i].data = MAX; for(i = setsize-1; i < treesize;i++) { tree[i].data= set[i - setsize + 1]; tree[i].index= i; } int p,l,r; p =(treesize-2)/2; while(p >= 0) { l = 2 * p + 1; r = 2 * p + 2; if(tree[l].data >tree[r].data) tree[p] = tree[r]; else tree[p] = tree[l]; p--;
	} return tree;
}

void printkth(TreeNode *tree, int kth)
{
	int index; int i; for(i = 0; i < kth; i++) { printf("the %dth is%d\n", i, tree[0].data); index = tree[0].index; tree[index].data = MAX; adjustTree(tree, index); }
}

void  adjustTree(TreeNode *tree, int index)
{
	int p,l,r; p = (index-1) / 2; while(p >= 0) { l = 2 * p + 1; r = 2 * p + 2; if(tree[l].data >tree[r].data) tree[p] = tree[r]; else tree[p] = tree[l]; if(p > 0) p = (p-1)/2; else break;
	}
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73

淘汰树

对于胜者树来说，在节点上升的时候首先需要获得父节点，然后再获得兄弟节点，然后再比较。这时人们又想能否减少访存次数，于是就有了败者树。

在败者树中，用父结点记录其左右子结点进行比赛的败者，让胜者参加下一轮的比赛。败者树的根结点记录的是败者，因此，需要加一个结点来记录比赛的最终胜者。

败者树重构过程如下：①首先，将新进入败者树的新结点与其父结点进行比较，并将败者存放在父结点中；②然后，将第1步中比较后的胜者再与上一级的父结点比较。

因为重构时覆盖原来叶子节点的下一个节点都比原叶子节点小，这里的小是指胜利的反方向，所以只要和败者比即可。此时父节点记录的就是败者，因此，只要和父节点比较即可。所以说对于败者树来说，它只要访问父节点，这是败者树的优势。

难点突破

晕不？我也晕呐，看了半天我才缓过来，值小的为胜者，值大的为败者。。。。。
把这个观念扭过来，然后我们再看。

这是一张比较经典的图，大家都在用：
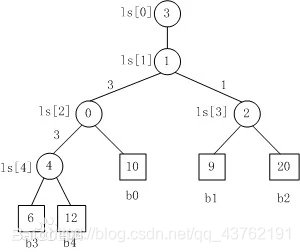
在这里插入图片描述

  a：b3 Vs b4，b3胜b4负，内部结点ls[4]的值为4，表示b4为败者；胜者b3继续参与竞争。
  b：b3 Vsb0，b3胜b0负，内部结点ls[2]的值为0，表示b0为败者；胜者b3继续参与竞争。
  c：b1 Vs b2，b1胜b2负，内部结点ls[3]的值为2，表示b2为败者；胜者b1继续参与竞争。
  d：b3 Vs b1，b3胜b1负，内部结点ls[1]的值为1，表示b1为败者；胜者b3为最终冠军，用ls[0]=3，记录的最后的胜者索引。
  • 1
  • 2
  • 3
  • 4

捋一下？捋清楚思路我们再往下，搞红黑树的时候都没这么折磨人，小者为胜，这个思想要扭过来。

淘汰树代码实现

void Adjust(int s)
{
	int t=(s+k)/2;   //t为内部结点，也就是s的父节点 while(t>0){ if(b[s]>b[ls[t]]){ int tmp=s; s=ls[t]; //s记录新的胜者 ls[t]=tmp; } t=t/2;
	} ls[0]=s;
}
 
void  CreateLoserTree()
{
	int i; b[k]=MIN; for(i=0;i<k;i++) ls[i]=k; for(i=k-1;i>=0;i--) Adjust(i);
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26

难搞哦。。

在这里插入图片描述
在这里插入图片描述

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/113762221

（完）