在==时序分析==众多模型中,最为基础也是最为重要的有AR§模型,MA(q)模型,以及两者的结合ARMA(p,q)模型,同时考虑ARMA模型的平稳性,若有一个或多个根落于单位圆上,则此时的ARMA模型称作自回归单整移动平均过程,ARIMA(p,d,q)模型。

这里介绍Python绘制ACF和PACF图,进行模型定阶
导入模块
import sys
import os
import pandas as pd
import matplotlib.pylab as plt
%matplotlib inline
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.tsa.stattools import adfuller
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.api import qqplot
"""中文显示问题"""
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
加载数据
data = pd.read_excel("data.xlsx",index_col="年份",parse_dates=True)
data.head()
<style scoped> </style>
| xt | |
|---|---|
| 年份 | |
| 1952-01-01 | 100.00000 |
| 1953-01-01 | 101.60000 |
| 1954-01-01 | 103.30000 |
| 1955-01-01 | 111.50000 |
| 1956-01-01 | 116.50000 |
平稳性检验
时序图
data["diff1"] = data["xt"].diff(1).dropna()
data["diff2"] = data["diff1"].diff(1).dropna()
data1 = data.loc[:,["xt","diff1","diff2"]]
data1.plot(subplots=True, figsize=(18, 12),title="差分图")

时序图检验 - - 全靠肉眼的判断和判断人的经验,不同的人看到同样的图形,很可能会给出不同的判断。因此我们需要一个更有说服力、更加客观的统计方法来帮助我们检验时间序列的平稳性,这种方法,就是单位根检验。
单位根检验
print("单位根检验:\n")
print(ADF(data.diff1.dropna()))
单位根检验:
Augmented Dickey-Fuller Results
=====================================
Test Statistic -3.156
P-value 0.023
Lags 0
-------------------------------------
Trend: Constant
Critical Values: -3.63 (1%), -2.95 (5%), -2.61 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
**单位根检验** - -对其一阶差分进行单位根检验,得到:1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,本数据中,P-value 为 0.023,接近0,ADF Test result同时小于5%、10%即说明很好地拒绝该假设,本数据中,ADF结果为-3.156,拒绝原假设,即一阶差分后数据是平稳的。
白噪声检验
判断序列是否为非白噪声序列
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(data.diff1.dropna(), lags = [i for i in range(1,12)],boxpierce=True)
(array([11.30402, 13.03896, 13.37637, 14.24184, 14.6937 , 15.33042,
16.36099, 16.76433, 18.15565, 18.16275, 18.21663]),
array([0.00077, 0.00147, 0.00389, 0.00656, 0.01175, 0.01784, 0.02202,
0.03266, 0.03341, 0.05228, 0.07669]),
array([10.4116 , 11.96391, 12.25693, 12.98574, 13.35437, 13.85704,
14.64353, 14.94072, 15.92929, 15.93415, 15.9696 ]),
array([0.00125, 0.00252, 0.00655, 0.01135, 0.02027, 0.03127, 0.04085,
0.06031, 0.06837, 0.10153, 0.14226]))
通过P<α,拒绝原假设,故差分后的序列是平稳的非白噪声序列,可以进行下一步建模
模型定阶
现在我们已经得到一个平稳的时间序列,接来下就是选择合适的ARIMA模型,即ARIMA模型中合适的p,q。
第一步我们要先检查平稳时间序列的自相关图和偏自相关图。通过sm.graphics.tsa.plot_acf和sm.graphics.tsa.plot_pacf得到图形
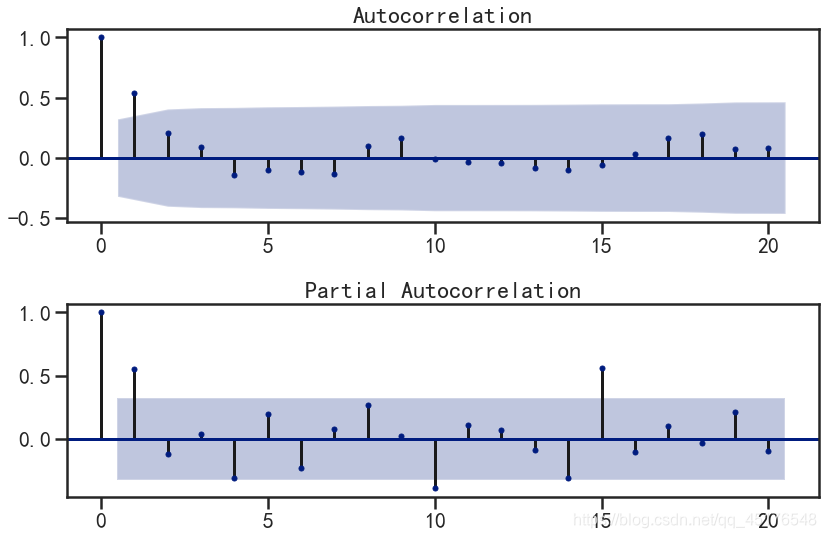
截尾是指时间序列的自相关函数(ACF)或偏自相关函数(PACF)在某阶后均为0的性质(比如AR的PACF);拖尾是ACF或PACF并不在某阶后均为0的性质(比如AR的ACF)。
==截尾==:在大于某个常数k后快速趋于0为k阶截尾
==拖尾==:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动)
从一阶差分序列的自相关图和偏自相关图可以发现:
- 自相关图拖尾或一阶截尾
- 偏自相关图一阶截尾,
- 所以我们可以建立ARIMA(1,1,0)、ARIMA(1,1,1)、ARIMA(0,1,1)模型。
def draw_acf_pacf(data):
"""
输入需要求解ACF\PACF的数据,
data["xt"]
"""
plt.rcParams['font.sans-serif'] = ['SimHei']
#模型的平稳性检验
"""时序图"""
plt.rcParams['font.sans-serif']=['SimHei']
data.plot(figsize=(12,8))
plt.legend(bbox_to_anchor=(1.25, 0.5))
plt.title("时序图")
fig = plt.figure(figsize=(12,8))
"""单位根检验"""
print("单位根检验:\n")
print(adfuller(data))
"""ACF"""
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data, lags=20,ax=ax1)
ax1.xaxis.set_ticks_position('bottom')
fig.tight_layout();
"""PACF"""
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data, lags=20, ax=ax2)
ax2.xaxis.set_ticks_position('bottom')
fig.tight_layout();
draw_acf_pacf(data["xt"])
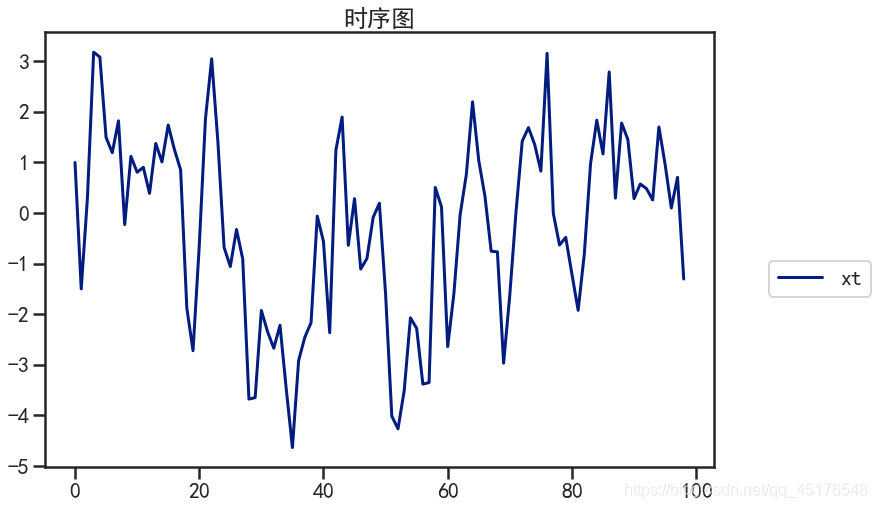
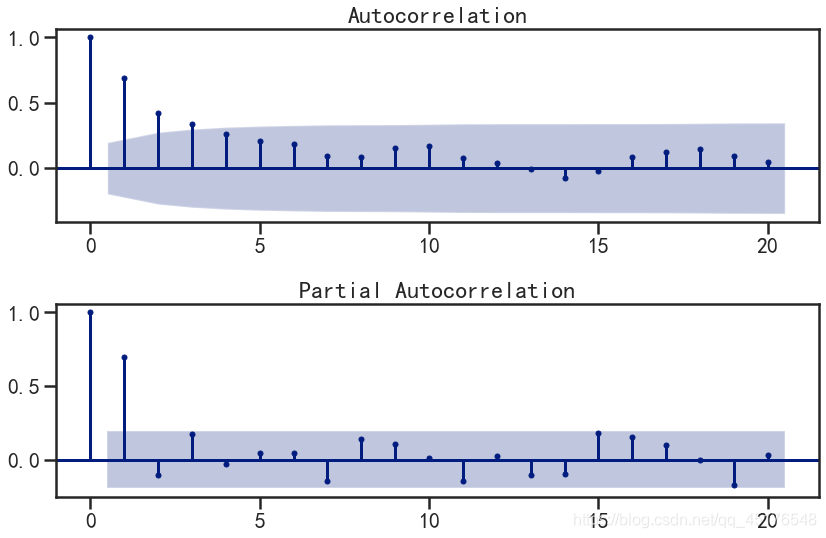
到这里就结束了,如果对你有帮助,欢迎点赞关注评论,你的点赞对我很重要,author:北山啦