【C++】算法集锦（4）：给人看的动态规划

在这里插入图片描述

文章目录

动态规划

动态规划问题，它不叫动态规划算法，因为它不是一种算法，它是一众类型的问题的统称。
我们前面两篇的“递归算法”、“回溯算法”，以及接下来会讲的“贪心算法”等都属于动态规划的范畴。

所以这一篇是会持续翻新的，每写一种相关文章，都会在这里呈现出来。

那么，到底什么是动态规划呢？

在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线．这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法。

动态规划解题步骤

不扯那些弯弯绕的。
第一步：画出暴力解法流程。
第二步：画出决策树（看着直观）
第三步：写出状态转移方程
第四步：决策树剪枝
第五步：再优化：确定边界

如果看了前面递归那篇的话，这里就不难理解了。【C++】算法集锦（2）：递归精讲
这五步列在这里，并不是说每一步都要严格的执行，我们的目标是解决问题，解决动态规划问题就需要状态转移方程，要写出好的状态转移方程就需要决策树以及决策树的剪枝优化，要画出决策树，最好有个暴力解的流程图。

不要看不起暴力求解，动态规划问题最困难的就是写出状态转移方程，即这个暴力解。优化方法无非是用备忘录或者 DP table，再无奥妙可言。

看一下上面递归那篇，里面的“爬楼梯”栗子。

老生常谈：凑零钱问题

先看下题目：给你 k 种⾯值的硬币，⾯值分别为 c1, c2 … ck ，每种硬币的数量无限，再给⼀个总金额 amount ，问你最少需要⼏枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。

比方说 k=3，面值分别为：1,2,5。总金额：8。

那么我们该如何来解决这个问题？

⾸先，这个问题是动态规划问题，因为它具有「最优子结构」的。

那么，既然知道了这是个动态规划问题，就要思考如何列出正确的状态转移方程？
先确定「状态」，也就是原问题和子问题中变化的变量。由于硬币数量无限，所以唯⼀的状态就是目标⾦额 amount 。

然后确定 dp 函数的定义：当前的⽬标⾦额是 n ，⾄少需要 dp(n) 个硬币凑出该金额。

然后确定「选择」并择优，也就是对于每个状态，可以做出什么选择改变当前状态。具体到这个问题，无论当的⽬标金额是多少，选择就是从面额列表 coins 中选择⼀个硬币，然后目标金额就会减少：

写出一个暴力解法伪代码：

def dp(n):
	if n == 0: return 0 
	if n < 0: return -1 # 求最⼩值，所以初始化为正⽆穷 
	res = float('INF') for coin in coins: subproblem = dp(n - coin) # ⼦问题⽆解，跳过 
		if subproblem == -1: continue res = min(res, 1 + subproblem) 
	return res if res != float('INF') else -1

⾄此，状态转移⽅程其实已经完成了：
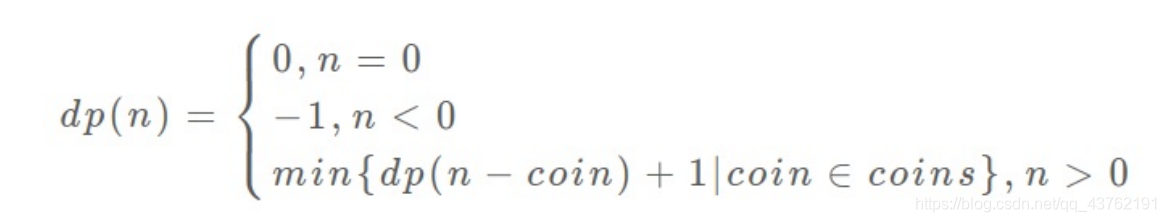
在这里插入图片描述

画出递归树看看：
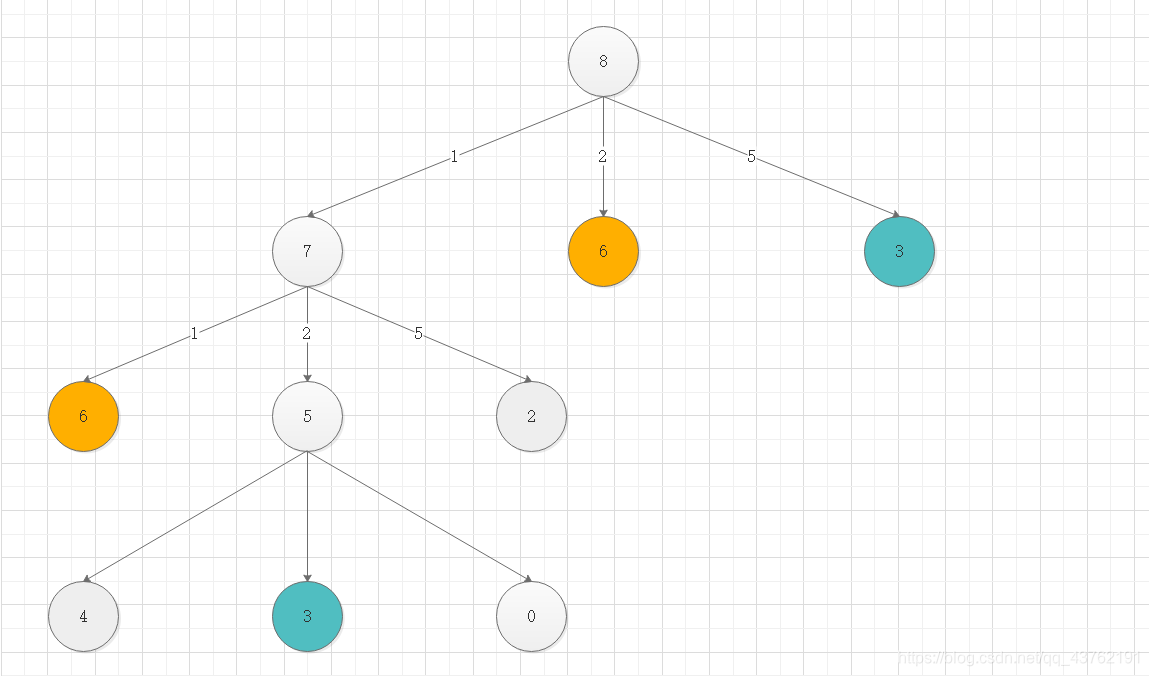
在这里插入图片描述

下面点点点。

所以我们使用备忘录来对决策树进行剪枝操作（上面剪过了）

memo = dict() 
def dp(n): 
	# 查备忘录，避免重复计算 
	if n in memo: return memo[n] 
	if n == 0: return 0 
	if n < 0: return -1 res = float('INF') 
	for coin in coins: subproblem = dp(n - coin) if subproblem == -1: continue res = min(res, 1 + subproblem) # 记⼊备忘录 
	memo[n] = res if res != float('INF') else -1 
	return memo[n]

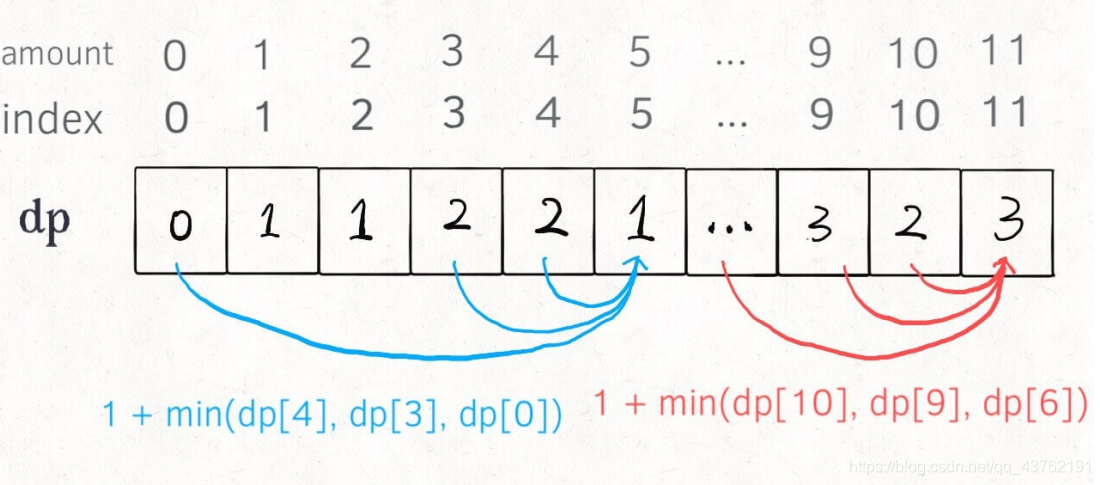
当然，我们也可以自底向上使用 dp table 来消除重叠子问题， dp 数组的定义和刚才 dp 函数类似，定义也是⼀样的： dp[i] = x 表示，当目标金额为 i 时，至少需要 x 枚硬币。

在这里插入图片描述

持续更新中。

在这里插入图片描述

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/113879544

（完）

文章目录

动态规划

动态规划解题步骤

老生常谈：凑零钱问题

其他和动归相关篇章