如题:
哥德巴赫猜想认为:不小于4的偶数都可以表示为两个素数的和。
你不需要去证明这个定理,但可以通过计算机对有限数量的偶数进行分解,验证是否可行。
实际上,一般一个偶数会有多种不同的分解方案,我们关心包含较小素数的那个方案。
对于给定数值范围,我们想知道这些包含较小素数方案中最大的素数是多少。
比如,100以内,这个数是19,它由98的分解贡献。
你需要求的是10000以内,这个数是多少?
注意,需要提交的是一个整数,不要填写任何多余的内容(比如,说明性的文字)
我先把素数统计下来。然后再对比。
#include <bits/stdc++.h>
using namespace std;
int main()
{ int i,j; int flag; int p[10000]; for(i=3;i<=10000;i++)//素数判断,制作素数表 { flag=1; for(j=2;j<=sqrt(i);j++) { if(i%j==0) { flag=0; break; } } if(flag) { p[i] = 1; } } int res=0; int x; for(int i=10000; i>=0; i-=2) { for(int j=2; j<=i/2; j++) { if(p[j]&&p[i-j]) { res=max(res,j); x=i; break; } } } printf("%d\n",res);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
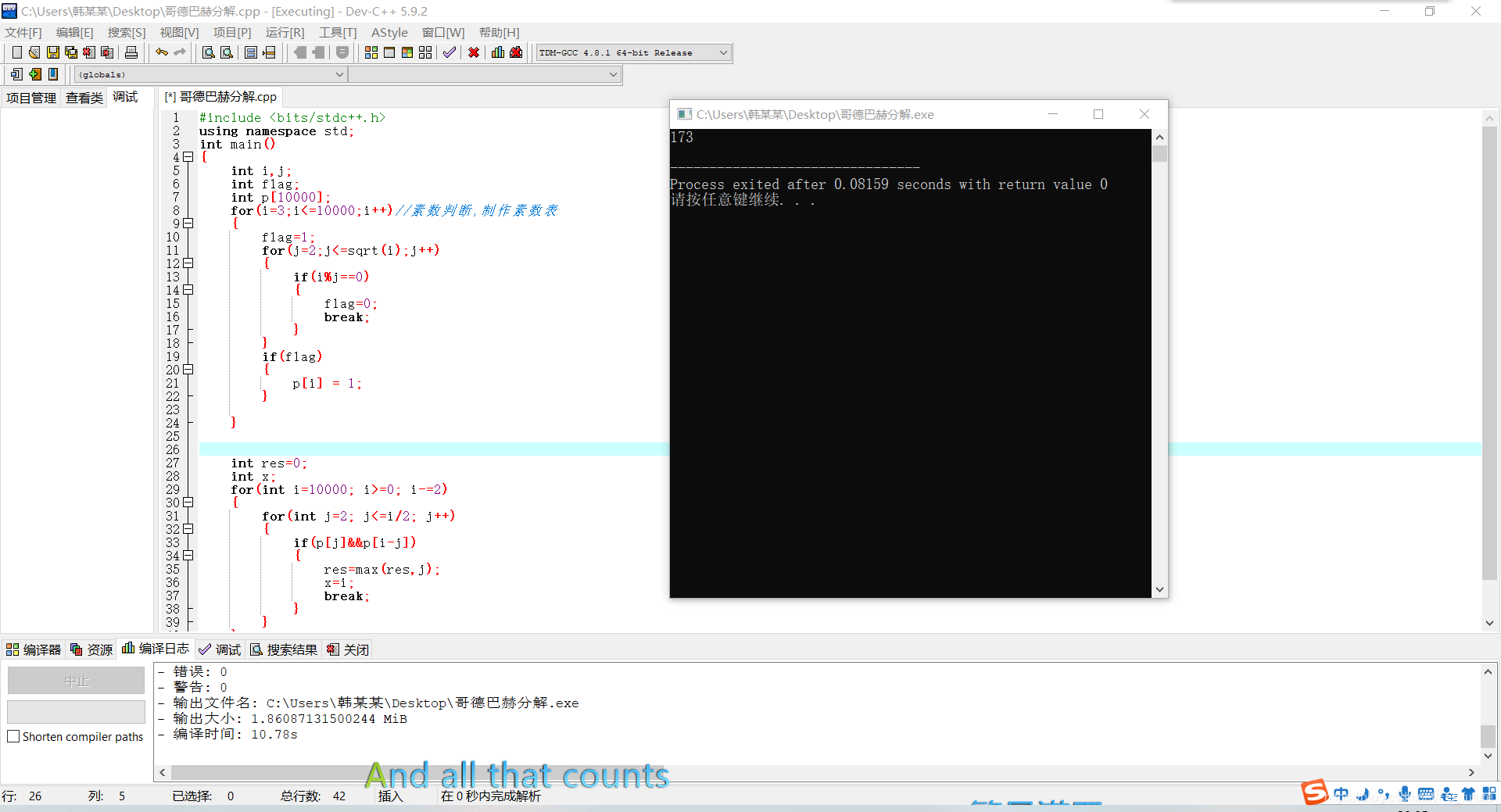
答案173
文章来源: blog.csdn.net,作者:i晴天,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/FG_future/article/details/113870970