【C++】算法集锦（10）通俗讲kmp算法

---

什么是KMP算法

它是一个字符串匹配算法。

KMP算法的优势

（就恨当初写kmp那篇的时候，没有留下图解，全篇文字铺开，现在我自己都看不懂了）

首先，给定 “主串” 和 “模式串” 如下：

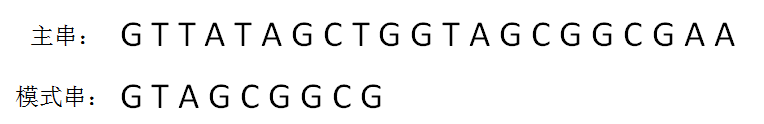
BF算法使用简单粗暴的方式，对主串和模式串进行逐个字符的比较：

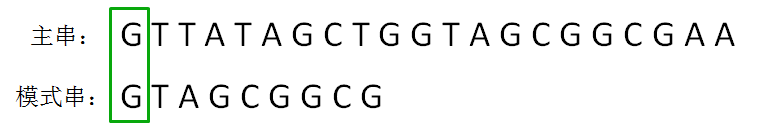
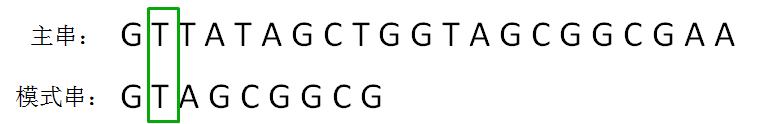
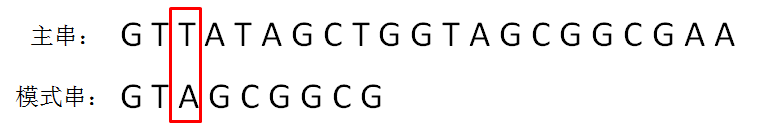
第二轮，模式串向后挪动一位，和主串的第二个等长子串比较，发现第0位字符不一致：

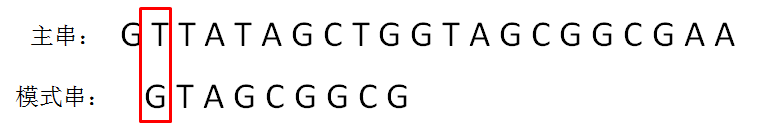
第三轮，模式串继续向后挪动一位，和主串的第三个等长子串比较，发现第0位字符不一致：

···
···

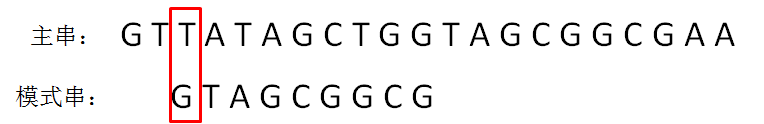
这种算法的缺点很明显，做了很多无谓的比较，还好，我们今天讲的不是这种算法。

---

KMP算法

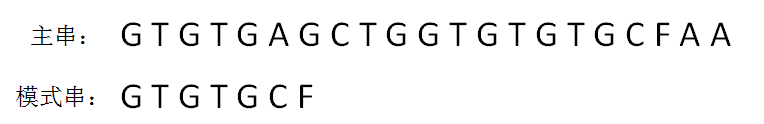
第一轮，模式串和主串的第一个等长子串比较，发现前5个字符都是匹配的，第6个字符不匹配，是一个“坏字符”：

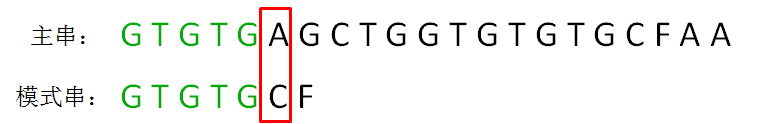
这时候，如何有效利用已匹配的前缀 “GTGTG” 呢？

我们可以发现，在前缀“GTGTG”当中，后三个字符“GTG”和前三位字符“GTG”是相同的：

在下一轮的比较时，只有把这两个相同的片段对齐，才有可能出现匹配。这两个字符串片段，分别叫做最长可匹配后缀子串和最长可匹配前缀子串。

第二轮，我们直接把模式串向后移动两位，让两个“GTG”对齐，继续从刚才主串的坏字符A开始进行比较：

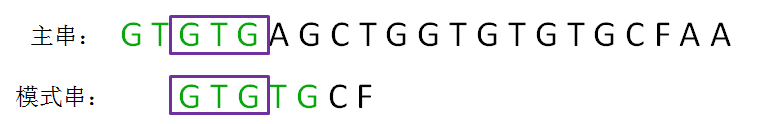
显然，主串的字符A仍然是坏字符，这时候的匹配前缀缩短成了GTG：

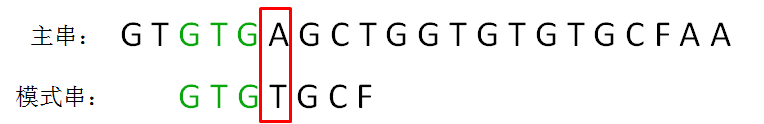
按照第一轮的思路，我们来重新确定最长可匹配后缀子串和最长可匹配前缀子串：

第三轮，我们再次把模式串向后移动两位，让两个“G”对齐，继续从刚才主串的坏字符A开始进行比较：

···
···

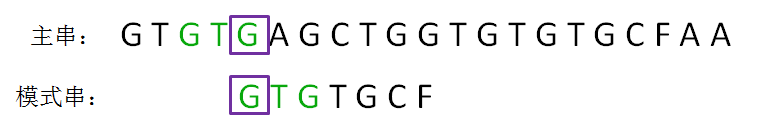
next数组

什么是next数组？next数组用来干什么？
next数组是决定kmp算法快速移动的核心。

好，我们来看一下next数组是如何生成的。

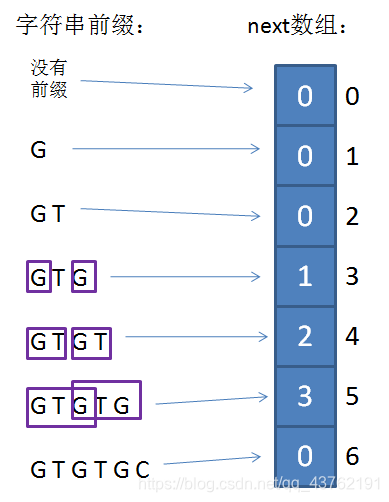
有了next数组，我们就可以通过已匹配前缀的下一个位置（坏字符位置），快速寻找到最长可匹配前缀的下一个位置，然后把这两个位置对齐。

比如下面的场景，我们通过坏字符下标5，可以找到next[5]=3，即最长可匹配前缀的下一个位置：

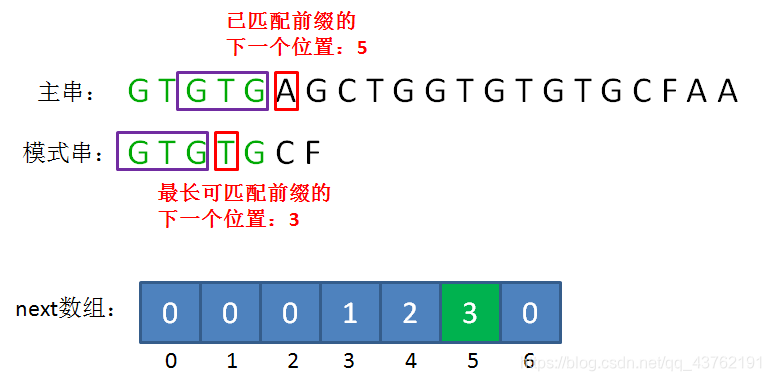
生成next数组

我先放一段代码再这里：
（如果用上面那张图里的方法，那生成next数组的过程是非常低效的）

void getnext(string p, vector<int> &next)	//next在传入时应该进行扩容
{
	int len = p.size();
	int k = -1;
	int j = 0;
	next[0]=-1;

	while (j < len - 1)
	{
		if (k == -1 || p[k] == p[j])
		{ k++; j++; next[j] = k;
		}
		else { k = next[k];
		}
	}
}

  

 

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20

能看懂吗？

首先为了后面运算方便，将next[0]设置为-1，不得不说这个设置为-1非常之巧妙。

先不说巧妙在哪里，自己去写的话就知道了。
也先不说那个令人绞尽脑汁的 k = next[k],我们先把基础弄明白。

先看next[j] = k，这一句。

来我们来个简单的栗子：“ababcba”.

要对这个子串求它的next数组，是这样的。

1、a
2、ab
3、aba
4、abab
5、ababc
6、ababcb
7、ababcba

  

 

• 1
• 2
• 3
• 4
• 5
• 6
• 7

将这个字符串这样分一下，然后对号入座，看到我标的号了没，对应的是next数组中的号，最后那个可以去掉，因为如果整个串都对上了还回溯什么。

首先我们来看一下“前后子集“的概念，我自己起的名字，还不错吧。

拿4来说把，它的前子集有：

{
	a,
	ab,
	aba
}

  

 

• 1
• 2
• 3
• 4
• 5

后子集有：

{
	b,
	ab,
	bab
}

  

 

• 1
• 2
• 3
• 4
• 5

规律不难找啊。

那，他俩子集里面有一个同类，“ab”，将ab的长度填入next[4]里面。

接下来难度要稍微升级了。

这个next数组，也有半自动推导，碧如说4（abab），它的对称度为2，那么如果在4的基础上，加上一个字符，这个字符刚好跟对称度+1的位置的字符对上，即如果加上的字符是a，那么便可以知道 5 的对称度为3，因为前面两个已经有 4 做了铺垫。
这就是：

if (k == -1 || p[k] == p[j])
{
	k++;
	j++;
	next[j] = k;
}

  

 

• 1
• 2
• 3
• 4
• 5
• 6

这一个部分的原理。next[++j] = ++k;,是这样来的。

可惜，上面那个例子加上去的是 ‘c’。那就·是另外一部分代码的事情了:

else {
	k = next[k];
}

  

 

• 1
• 2
• 3

---

k = next[k]

要理解这行代码，我们用另外一个字符串会比较直观一些。

“a b a b a b c b”

一步一步来啊，

1、a
next[0] = -1;
k = -1，j=0; 
k = 0，j=1;

next[1] = 0;	//进入了if
//这两个简直是铁索连环，就写一起吧

  

 

• 1
• 2
• 3
• 4
• 5
• 6
• 7

2、a,b
j = 1,k = 0; //进入else
k = -1;	//所以，嗯
//再一圈循环
k = 0,j = 2;	//进入if
next[2] = 0;

  

 

• 1
• 2
• 3
• 4
• 5
• 6

3、a,b,a
//进入if
k = 1,j = 3;
next[3] = 1;


  

 

• 1
• 2
• 3
• 4
• 5

4、a,b,a,b
k = 2,j = 4;
next[4] = 2;

//看啊，用到上面讲的了。
//其实还有一条铁律忘记说了，如果有耐心看到这里那我就说。后一位的对称度，顶多比前一位，多1！！！

  

 

• 1
• 2
• 3
• 4
• 5
• 6

5、a,b,a,b,a
k = 3,j = 5;
next[5] = 3;

  

 

• 1
• 2
• 3

6、a,b,a,b,a,b
k = 4,j = 6;
next[6] = 4;
//越来越接近目标了啊，马上就要断了香火了

  

 

• 1
• 2
• 3
• 4

7、a,b,a,b,*a*,b,c
// ‘c’!=‘a’!
// 进入else
k = next[4] = 2
// 循环，进入else
k = next[2] = 0
// 再循环，
k = -1
// 再循环，进入if
k = 0,j = 7
next[7] = 0

-----


这时候你会发现，它新加上来的那个字符，和对称度后面一位字符不匹配，‘c’!=‘a’!,那里我打了星标。


  

 

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17

KMP匹配、

这个匹配就比较好理解了，该注释的地方我注释了

int kmp(string s, string p)
{
	int i = 0;
	int j = 0;
	int sLen = s.size();
	int pLen = p.size();

	if (pLen == 0 )
		return 0;

	vector<int> vec(pLen, 0);
	getnext(p,vec);	//获取next数组

	while (i < sLen && j < pLen)
	{
		if (j == -1 || s[i] == p[j])
		{ i++; j++;
		}
		else
		{ //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]  //next[j]即为j所对应的next值  j = vec[j];
		}
	}
	if (j >= pLen)
		return(i - j);
	return -1;
}

  

 

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31

KMP算法整体实现（LeetCode测试通过）

#include<iostream>
#include<string>
#include<vector>

using namespace std;

void getnext(string p, vector<int> &next)	//next在传入时应该进行扩容
{
	int len = p.size();
	int k = -1;
	int j = 0;
	next[0]=-1;

	while (j < len - 1)
	{
		if (k == -1 || p[k] == p[j])
		{ k++; j++; next[j] = k;
		}
		else { k = next[k];
		}

	}

}


int kmp(string s, string p)
{
	int i = 0;
	int j = 0;
	int sLen = s.size();
	int pLen = p.size();

	if (pLen == 0 )
		return 0;

	vector<int> vec(pLen, 0);
	getnext(p,vec);	//获取next数组

	while (i < sLen && j < pLen)
	{
		if (j == -1 || s[i] == p[j])
		{ i++; j++;
		}
		else
		{ //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]  //next[j]即为j所对应的next值  j = vec[j];
		}
	}
	if (j >= pLen)
		return(i - j);
	return -1;
}


int main()
{	
	vector<int> vec1(10,0);
	//for (int i = 0; i < vec1.size(); i++)
	//	cout << vec1[i] << " ";
	//cout << endl;

	string str = ""; string str2 = "";

	int a = kmp(str,str2);
	cout << a << endl;

	/*getnext(str2,vec1);

	for(int i = 0;i<vec1.size();i++)
		cout << vec1[i]<<" ";
	cout << endl;*/
}

  

 

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83

---

注：图来自《小灰的漫画算法之旅》

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/114020996