为实习准备的数据结构（5）-- 图解AVL树（平衡二叉搜索树）

在这里插入图片描述

文章目录

前言

之前种过AVL树，为什么要再写呢？依旧是因为我忘了，重刷一遍呗。

平衡二叉搜索树（AVL树）

二叉搜索树一定程度上可以提高搜索效率，但是当原序列有序，例如序列A = {1，2，3，4，5，6}，构造二叉搜索树如图。依据此序列构造的二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为O(n)。

如下图：
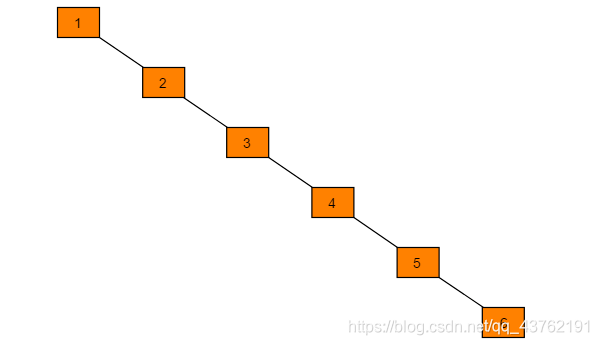
在这里插入图片描述

在此二叉搜索树中查找元素6需要查找6次。二叉搜索树的查找效率取决于树的高度，因此保持树的高度最小，即可保证树的查找效率。同样的序列A，改为下图方式存储，查找元素6时只需比较3次，查找效率提升一倍。

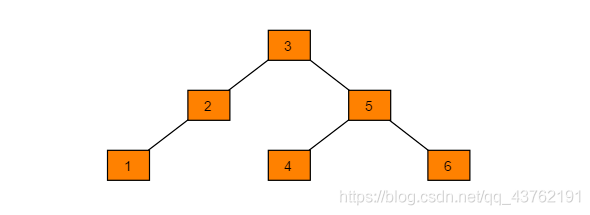
在这里插入图片描述

可以看出当节点数目一定，保持树的左右两端保持平衡，树的查找效率最高。这种左右子树的高度相差不超过1的树为平衡二叉树。

AVL树的节点数据结构

和上面使用的那个普通结构略有不同。

class TreeNode{
public:
	//这几个数据放做公有的，方便操作 int depth; //深度，这里计算每个结点的深度，通过深度的比较可得出是否平衡 TreeNode* parent; //该结点的父节点，方便操作 int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), depth(0), left(NULL), right(NULL) {} TreeNode() : val(0), depth(0), left(NULL), right(NULL) {}
};

在原始数据上创建AVL树

我的代码尝试：
（先对原始数据进行排序，然后再填充二叉搜索树，使用递归的方式。）

#include<iostream>
#include<vector>
using namespace std;

void createTree(vector<int>& vec, TreeNode* root, int begin, int end) { //如果只剩一个键 if (begin == end) { root->val = vec[begin]; return; } int mid_sz = (begin+end)/2; root->val = vec[mid_sz]; if (mid_sz - 1 >= begin) { root->left = new TreeNode(0); createTree(vec, root->left, begin, mid_sz - 1); } root->right = new TreeNode(0); createTree(vec, root->right,mid_sz + 1,end);
}

void PreOrderTraverse(TreeNode* root) { if (NULL == root) return; cout << root->val; PreOrderTraverse(root->left); PreOrderTraverse(root->right);
}

int main() { TreeNode* roott = new TreeNode(0); vector<int> vec = { 0,1,2,3,4,5,6,7}; createTree(vec,roott,0,vec.size()-1); PreOrderTraverse(roott);
}

调整树的节点使平衡的操作：旋转

LL （右旋）：在左叶的左侧插入数据

图解过程：
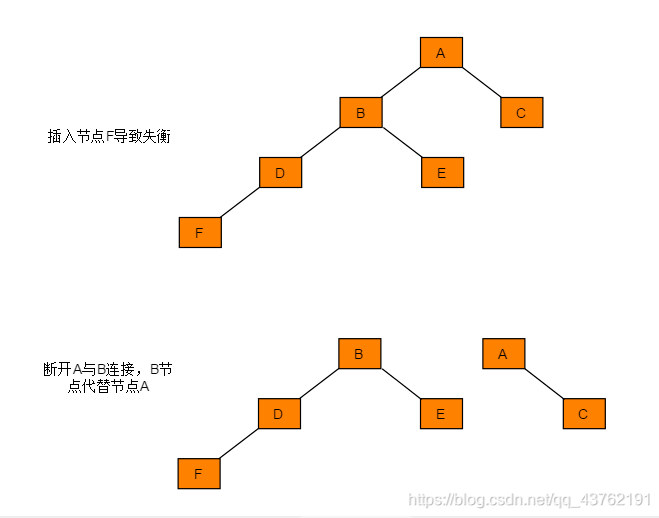
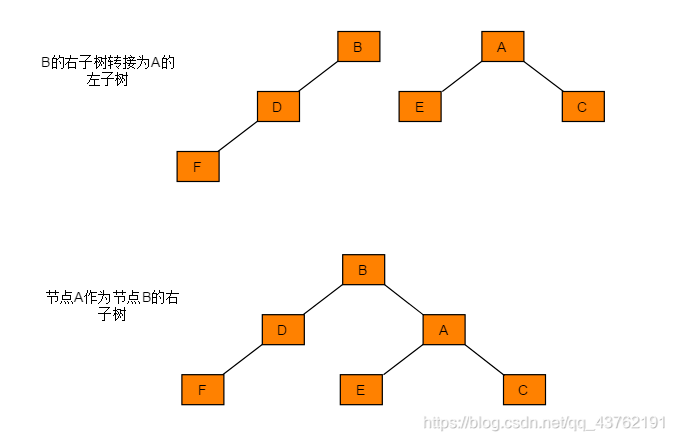
在这里插入图片描述

在这里插入图片描述

代码实现：

//在左叶的左侧插入数据
TreeNode* LL(TreeNode* root) { TreeNode* x = root->left;	//即将返回的节点是y的左子节点（就是那个B） TreeNode* temp = x->right;	//先把y的右子节点取出来（就是那个E） x->right = root;			//把y放进x的右子节点（把A放到B的右节点） root->left = temp;			//把前面预存的放到y的左子节点（把E放到A的右节点） return x; //(返回那个B)
}

int main() { TreeNode* roott = new TreeNode(0); vector<int> vec = { 0,1,2,3,4,5,6,7}; createTree(vec,roott,0,vec.size()-1); roott = LL(roott); PreOrderTraverse(roott);
}

RR（左旋）：在右子叶的右侧插入数据

图解过程：
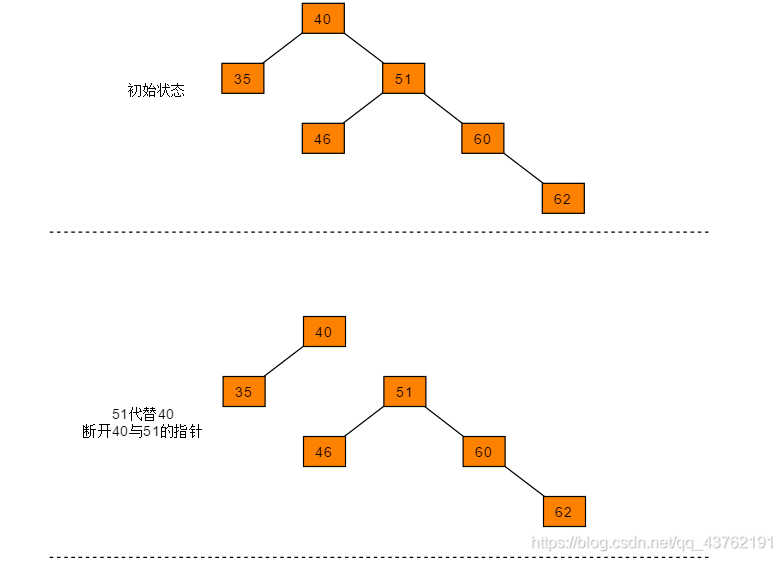
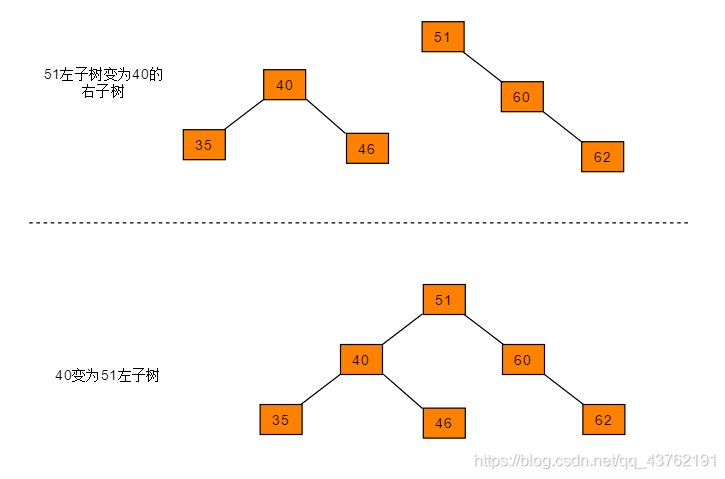
在这里插入图片描述

右旋其实就是上面左旋的镜像过程，所以不难，直接仿写上面左旋的过程即可：

代码实现

TreeNode* RR(TreeNode* root) { TreeNode* x = root->right;	//即将返回的节点是y的右子节点 TreeNode* temp = x->left;	//先把x的左子节点取出来 x->left = root;			//把y放进x的左子节点 root->right = temp;			//把前面预存的放到y的右子节点   return x;
}

int main() { TreeNode* roott = new TreeNode(0); vector<int> vec = { 0,1,2,3,4,5,6,7}; createTree(vec,roott,0,vec.size()-1); roott = RR(roott); PreOrderTraverse(roott);
}

后面的部分，就比较抽象了。

LR（左右旋）：在左叶节点的右侧插入数据

在这里插入图片描述

我们将这种情况抽象出来，得到下图：
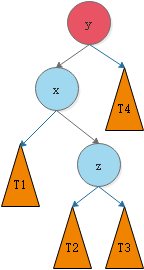
在这里插入图片描述

我们需要对节点y进行平衡的维护。步骤如下图所示（第三个图里面x和z的位置换一下。）：
在这里插入图片描述

代码实现

TreeNode* LR(TreeNode* root) {
	root->left = RR(root->left);
	root = LL(root);
	return root;
}
//简单明了啊

RL（右左旋）：在右叶节点的左侧插入数据

在这里插入图片描述

我们将这种情况抽象出来，得到下图：

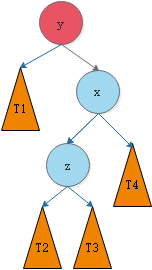
在这里插入图片描述

我们需要对节点y进行平衡的维护。步骤如下图所示（第三个图里面x和z的位置换一下。）：
在这里插入图片描述

第二个图中y的左孩子为T1
（被水印遮住的部分为：T1，T2，T3，T4）

代码实现

TreeNode* RL(TreeNode* root) { root->right = LL(root->right); root = RR(root); return root;
}
//简单明了啊

新节点的插入

在这里需要先补两个函数，虽然可能现在看不懂，但是配上调用函数的上下文就懂了。

计算平衡因子

int getBalanceFactor(TreeNode* node){
	if(node==NULL){
		return 0;
	}
	return get_depth(node->left)-getHeight(node->right);
}

int get_depth(TreeNode* node){
	if(node==NULL){
		return 0;
	}
	return node->depth;
}

对getBalanceFactor函数返回值的分析：

如果刚插入的叶子节点的爷爷节点的返回值大于0
1. 如果刚插入的叶子节点的父节点的返回值大于0：(LL)
2. 如果刚插入的叶子节点的父节点的返回值小于0：(LR)
如果刚插入的叶子节点的爷爷节点的返回值小于0
1. 如果刚插入的叶子节点的父节点的返回值大于0：(RL)
2. 如果刚插入的叶子节点的父节点的返回值小于0：(RR)

正式插入新节点

TreeNode* Insert_Node(TreeNode* root, int val) { //先将节点插入 if (NULL == root) return new TreeNode(val); else { if (val < root->val) root->left = Insert_Node(root->left, val); else root->right = Insert_Node(root->right, val); } //计算平衡因子 int balanceFactor = getBalanceFactor(root); //判断是否该旋转，该如何旋转 if (balanceFactor > 1) { //左子树有事儿 balanceFactor = getBalanceFactor(root->left); if (balanceFactor == 1) //插左边了 return LL(root); else if (balanceFactor == -1)   //插右边了 return RR(root); else { cout << "罕见故障" << endl; } } else if (balanceFactor < -1) {  //右子树有事儿 balanceFactor = getBalanceFactor(root->right); if (balanceFactor == 1) //插左边了 return RL(root); else if(balanceFactor == -1)   //插右边了 return RR(root); else { cout << "罕见故障" << endl; } } return root;
}

int main() { TreeNode* roott = new TreeNode(0); vector<int> vec = { 0,1,2,3,4,5,6,7}; createTree(vec,roott,0,vec.size()-1); roott = Insert_Node(roott,8); PreOrderTraverse(roott);
}

现有节点删除

代码里的注释把整个过程写的已经很详尽了。

//删除节点
TreeNode* DelSerchNode(TreeNode* node, int e) { if (node == NULL) return NULL; TreeNode* retNode; if (e < node->val) { node->left = DelSerchNode(node->left, e); retNode = node; } else if (e > node->val) { node->right = DelSerchNode(node->right, e); retNode = node; } else { // 待删除节点左子树为空的情况 if (node->left == NULL) { TreeNode* rightNode = node->right; node->right = NULL; retNode = rightNode; } // 待删除节点右子树为空的情况 else if (node->right == NULL) { TreeNode* leftNode = node->left; node->left = NULL; retNode = leftNode; } else { // 待删除节点左右子树均不为空的情况 // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点 // 用这个节点顶替待删除节点的位置 TreeNode* temp = node; while (NULL != temp->left) { temp = temp->left; } node->val = temp->val; node->left = NULL; //temp = NULL;  //这还删不掉了。。。。这指针还真是顽强 delete temp; retNode = node; } } if (retNode == NULL) return NULL; //计算平衡因子 int balanceFactor = getBalanceFactor(retNode); //判断是否该旋转，该如何旋转 if (balanceFactor > 1) { //左子树有事儿 balanceFactor = getBalanceFactor(retNode->left); if (balanceFactor == 1) //插左边了 return LL(retNode); else if (balanceFactor == -1)   //插右边了 return RR(retNode); else { cout << "罕见故障" << endl; } } else if (balanceFactor < -1) {  //右子树有事儿 balanceFactor = getBalanceFactor(retNode->right); if (balanceFactor == 1) //插左边了 return RL(retNode); else if (balanceFactor == -1)   //插右边了 return RR(retNode); else { cout << "罕见故障" << endl; } } return retNode;
}

int main() { TreeNode* roott = new TreeNode(0); vector<int> vec = { 0,1,2,3,4,5,6,7}; createTree(vec,roott,0,vec.size()-1); roott = DelSerchNode(roott,5); PreOrderTraverse(roott);

先到这里吧。

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/113742259

（完）