[LeetCode] Count Primes - 素数系列问题

题目概述：

Description:Count the number of prime numbers less than a non-negative number, n.

解题方法：

题意是给出n中所有素数的个数。
首先你需要知道判断一个数是不是素数的方法：（最笨方法但有效）

bool IsPrime(int n)  
{  
    if (n<2) {  //小于2的数即不是合数也不是素数 
        return false;  
    }  
    //和比它小的所有的数相除,如果都除不尽则证明素数
    for(int i=2; i<n; i++) {   
        if (n%i==0) {  
            return false;  //除尽则是合数  
        }  
    }  
    return true;  
}

更多数学方面关于素数判断问题，参考博客：算法总结：判断一个数是否为素数
最初想法是通过两层循环依次判断n个数里素数个数，但代码显然会TLE。当n=499979时就Time Limit Exceeded，超时代码如下：

int countPrimes(int n) {
    int count=0;
    int i,j;
    int number;
    
    if(n<=1) return 0;
    for(i=2; i<n; i++) {
        //分别判断i是不是素数
        number = i;
        for(j=2; j<i; j++) {
            if(number%j==0) {
                //除尽表示不是素数
                break;
            }
        }
        count++;
    }
    return count;
}

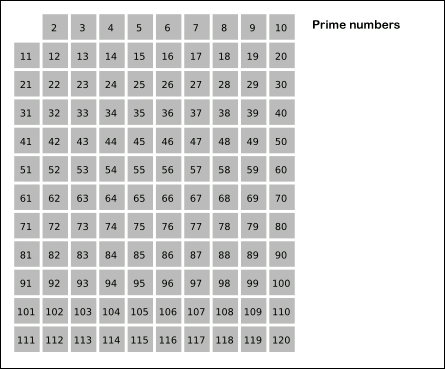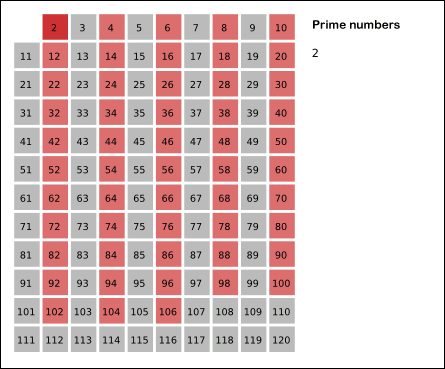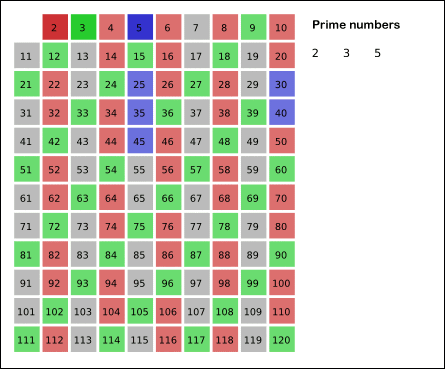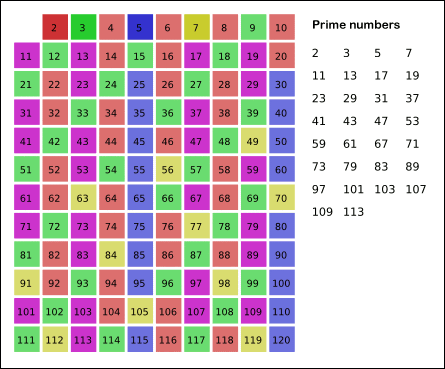
后来找到一种方法，只能说是Perfect。它叫做Sieve of Eratosthenes(埃拉托色尼筛法，简称埃氏筛法)，参考维基百科：Sieve of Eratosthenes

它的思想是通过建立一个bool型数组，从2开始计数，其倍数的数字都赋值为true，显然不是素数。最后统计false的个数即为素数个数。

我的代码：

/**
 * 题意：计算n中的素数个数
 * <span style="font-family: Arial, Helvetica, sans-serif;">第二种方法 Sieve of Eratosthenes 埃拉托色尼筛法，简称埃氏筛法</span>
 * By: Eastmount 2015-9-21
 */ 
int countPrimes(int n) {
    int count;
    int i,j;
    bool *nums;
    
    if(n<=1) return 0;
    
    //动态数组nums记录是否为素数
    nums = (bool*)malloc(sizeof(bool)*n);
    for(i=2; i<n; i++) {
        //i的倍数均非素数
        if(!nums[i]) { 
            for(j=2; j*i<n; j++) {
                nums[j*i] = true;
            }
        }
    }
    
    //计算素数个数
    count = 0;
    for(i=2; i<n; i++) {
        if(nums[i]==false) {
            count++;
        }
    }
    free(nums);
    return count;
}

类似题目：

Ugly Number
Ugly numbers are positive numbers whose prime factors only include 2, 3, 5. For example, 6, 8 are ugly while 14 is not ugly since it includes another prime factor 7.
Note that 1 is typically treated as an ugly number.
题意：就是子数由2、3、5组成的数字即为Ugly数字，6=2*3、8=2*2*2。

bool isUgly(int num) {
    //丑数具有如下特征：1是丑数，丑数可以表示为有限个2、3、5的乘积
    int result=0;
    if(num<=0)  //防止Last executed input:0 超过时间限制
        return false;
    while(num!=1) {
        if(num%2==0) {
            num=num/2;
        }
        else if(num%3==0) {
            num=num/3;
        }
        else if(num%5==0) {
            num=num/5;
        }
        else {
            result=1;
            break;
        }
    }
    if(result==1)
        return false;
    else
        return true;
}

该方法真的好友技巧啊！只能说算法真是博大精深，同时最近360的笔试题目也考到了一个数字由两个素数组成并打印成5*3的图形题目。所以还是挺重要的知识。2015年的文章，希望您喜欢。

原文地址：https://blog.csdn.net/Eastmount/article/details/48617469

(By:Eastmount 2021-7-31 夜于武汉)

（完）