什么是并查集
并查集这种数据结构,可能出现的频率不是那么高,但是还会经常性的见到,其理解学习起来非常容易,通过本文,一定能够轻轻松松搞定并查集!
对于一种数据结构,肯定是有自己的应用场景和特性,那么并查集是处理什么问题的呢?
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题,常常在使用中以森林来表示。在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
你可能还有点迷糊并查集能怎么玩,看完这篇然后回头看这两个问题(分别杭电1232和杭电1272)。
问题1:
某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。问最少还需要建设多少条道路?
这个问题很容易,给定的关系看看需要合并多少次就知道最少的建设道路数量。
问题二:
小希希望任意两个房间有且仅有一条路径可以相通(除非走了回头路)。小希现在把她的设计图给你,让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子,前两个是符合条件的,但是最后一个却有两种方法从5到达8。
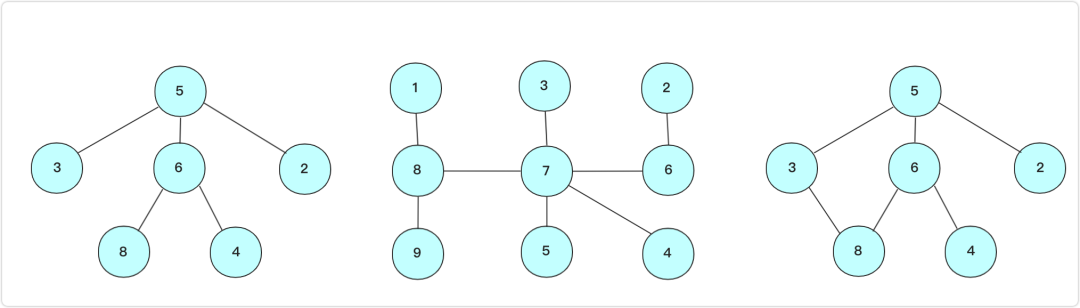
这个问题也很容易了,根据关系集合进行合如果两个元素已经属于一个集合,那就说明不满足要求啦。
并查集解析
通过上面介绍,相信你已经清楚并查集就是解决集合中一些元素的合并和查询问题,现在就带你解析这个算法。
初始化
开始时候森林中每个元素没有任何操作,它们之间是相互独立的。我们通常会使用数组来表示这个森林(数组下标对应第几个元素),在初始化的时候数组中的各个值为-1,表示各自自己是一个集合(各自为王),你可能会问为啥是-1而不是一个其他的数,那是因为用负数可以代表这个元素是某个集合的根,然后它的权值表示集合中元素的个数。
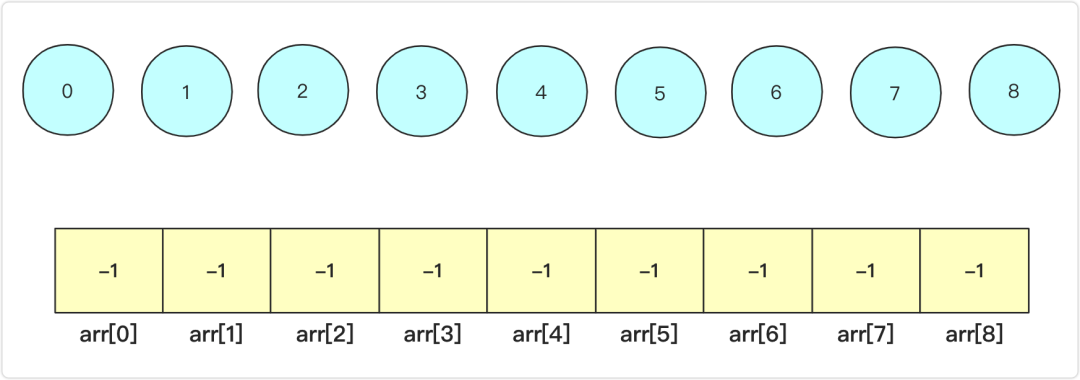
并 union(int a,int b)
这里合并,并没有你想象的直接合并那么简单,这里合并是合并a所在的集合和b所在的集合,但在操作层面a,b可能并不是根节点,所以也要先判断一下。
为了便于理解,这里罗列一下最初操作可能的情况,初始时候各个元素都是独立的集合,那么直接a指向b(或者b指向a)即arr[a]=b,同时为了表示这个集合有多少个,原本-1的b再次-1.即arr[b]=-2.表示以b为父根的集合节点有|-2|个。例如进行union(1,4),union(5,7)操作之后如图所示:
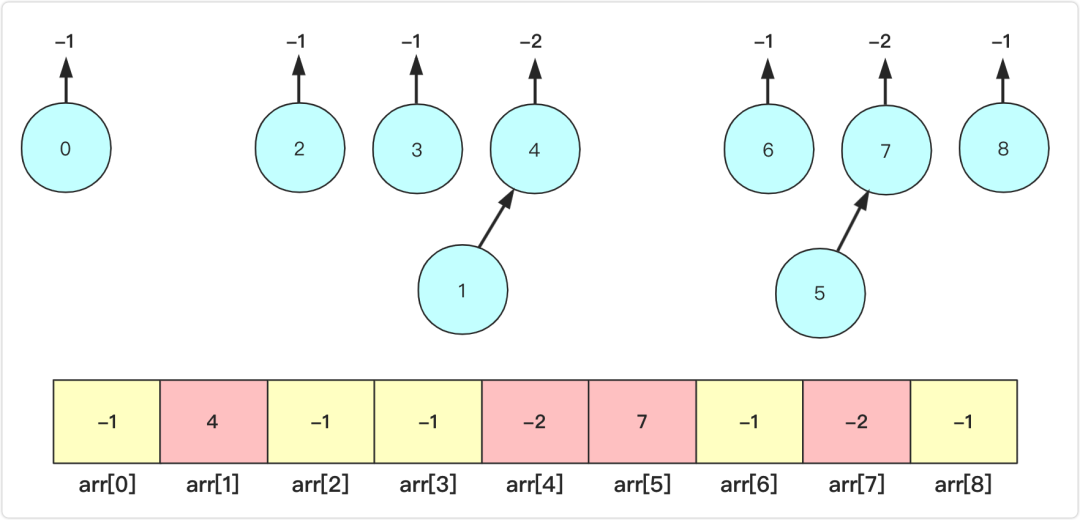
正常情况的union(int a,int b),假设我们就是a合并到b上,把b当成父集合来看。a、b都可能是叶子节点,也可能是根节点。
此时你可以先分别找到a,b的父节点fa,fb(这个根可能是它自己),然后合并fa和fb两个节点,例如上面如果union(1,5)那么其实就是等价union(4,7)。
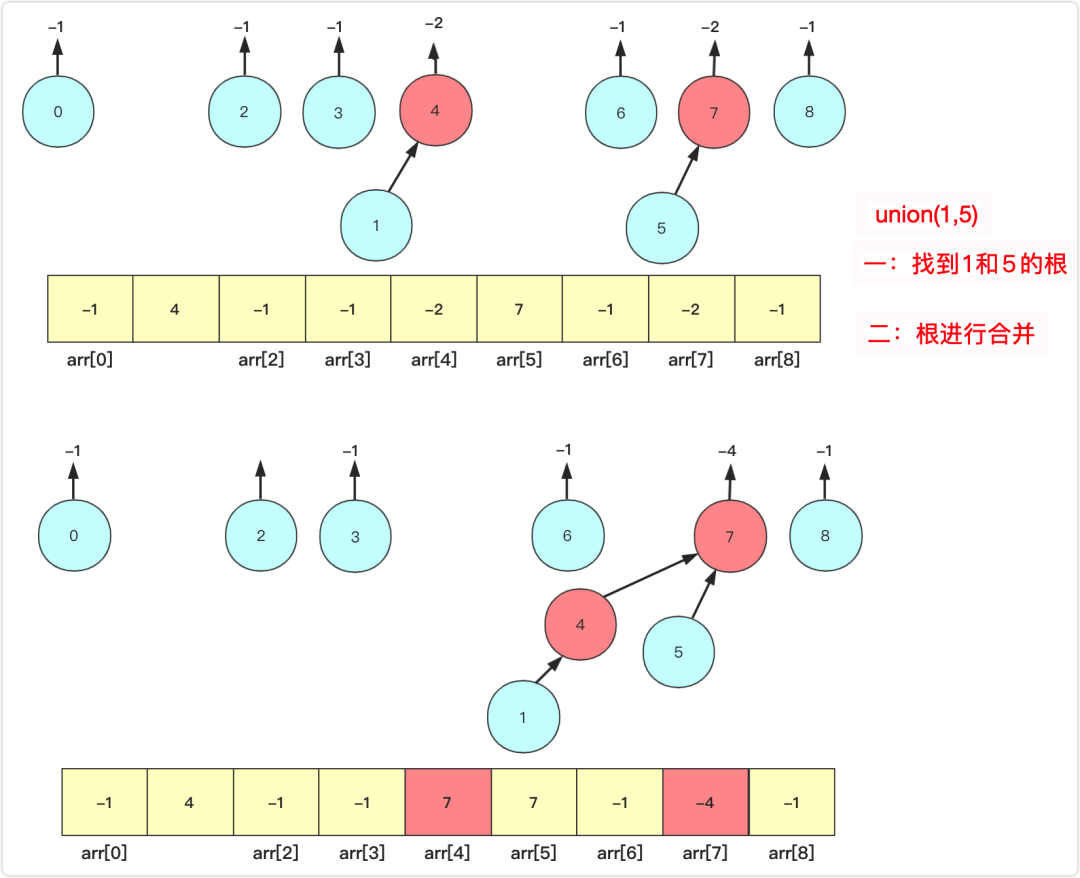
为什么不直接操作a,b而是要找到他们的父亲进行操作?
原因1是因为a,b可能是叶子节点,其值是正的表示已经有父亲了,如果直接操作会使其与原来的集合分离开。另外集合中的数量(负数)也不能有效叠加。
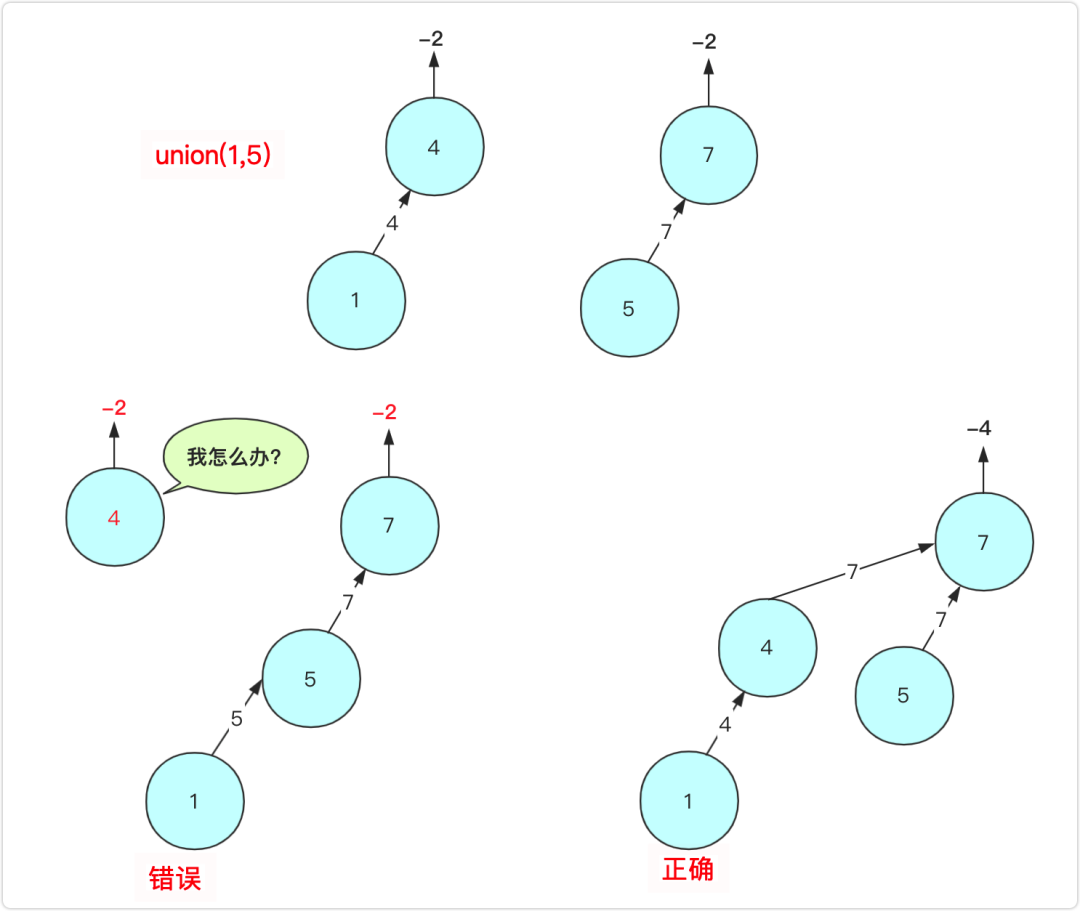
原因2是因为合并的时候如果合并如果a,b是非根节点操作,可能会造成这个树的深度太大,不利于集合a中的查询效率。
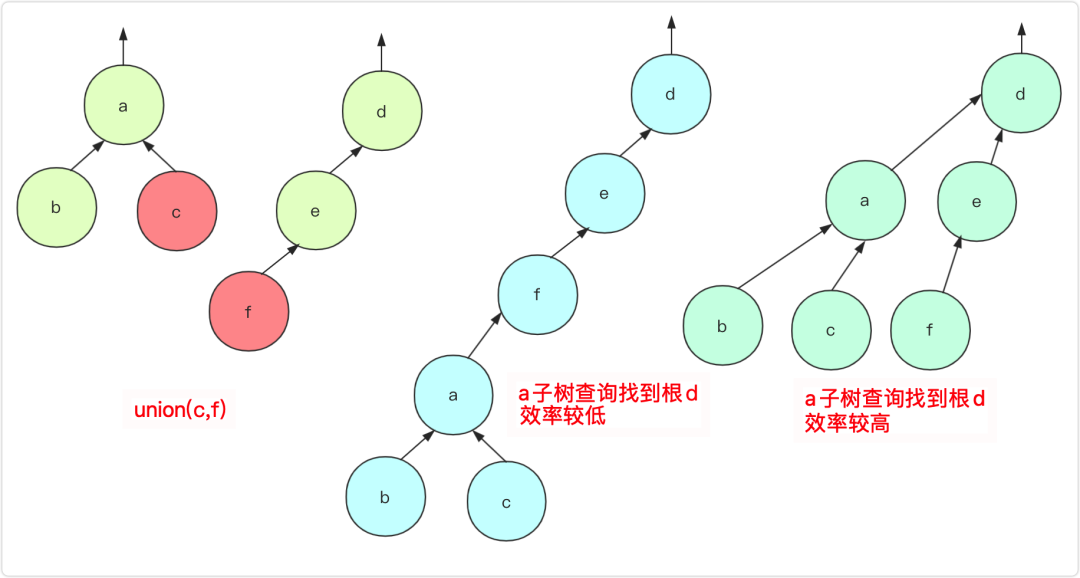
查 search(int a)
查询,其实就是查询这个节点的根节点是啥(也称代表元),这个过程也有点类似递归的过程,叶子节点值如果为正,那么就继续查找这个值得位置的结果,一直到值为负数的时候说明找到根节点,可以直接返回。
不过在查询的过程中可以顺便路径优化,这样在频繁查询能够大大降低时间复杂度。
优化
你以为上面的就是并查集的全部?不不不,并查集还有不少需要掌握嘞,估计细心的人可能也会发现一些问题。
你可能会有疑问:
如何查看a,b是否在同一个集合?
查看是否在一个集合,只需要查看节点根祖先的结果是否相同即可。因为只有根的数值是负的,而其他都是正数表示指向的元素。所以只需要一直寻找直到不为正数进行比较即可!
a,b合并,究竟是a的祖先合并在b的祖先上,还是b的祖先合并在a上?
这里会遇到两种情况,这个选择也是非常重要的。你要弄明白一点:树的高度+1的化那么整个元素查询的效率都会降低!
所以我们通常是:小树指向大树(或者低树指向高树),这个使得查询效率能够增加!
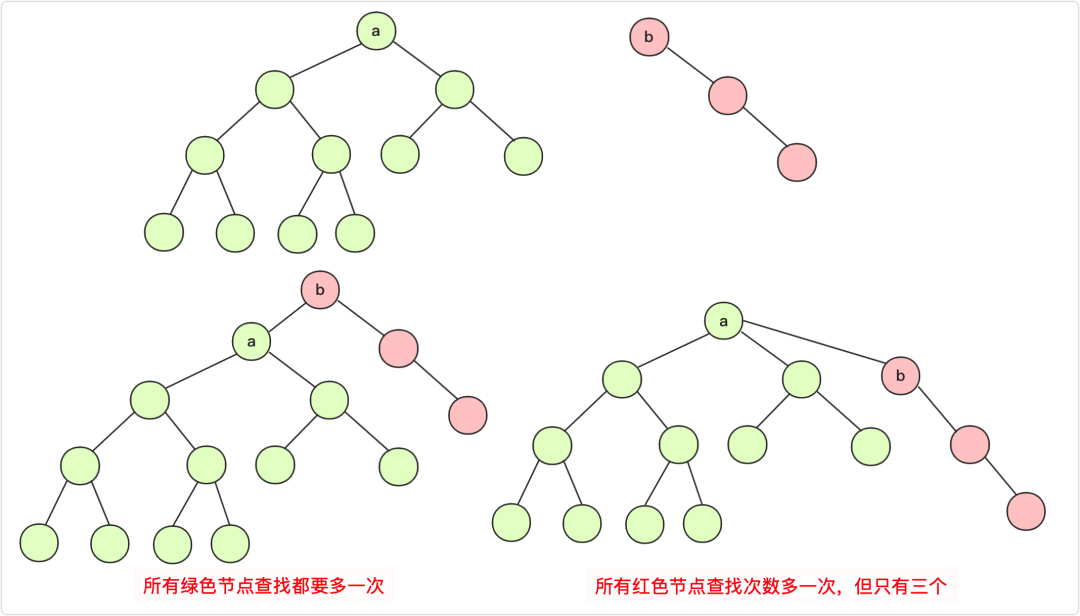
当然,在高度和数量的选择上,还需要你自己选择和考虑。
查找途中能不能路径压缩
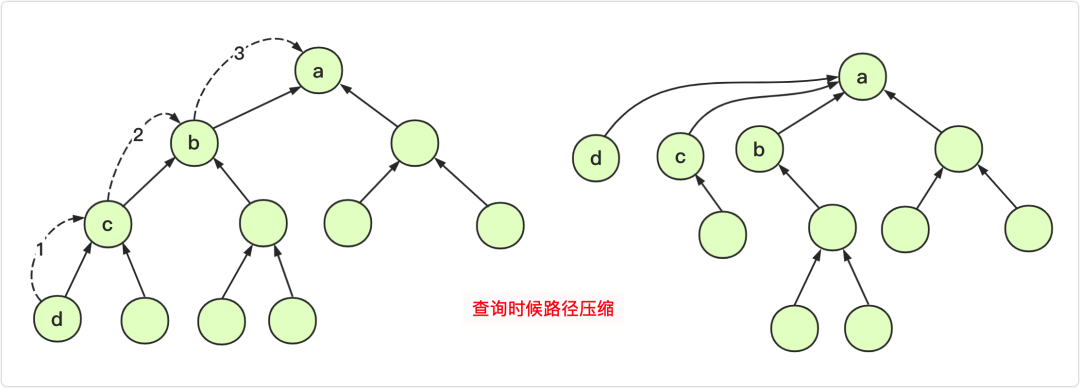
每次查询,自下向上。当我们调用递归的时候,可以顺便压缩路径(将当前数组的值等于递归返回的根节点的值),我们查找一个元素只需要直接找到它的祖先,所以当它距离祖先近那么下次查询就很快。并且压缩路径的代价并不大!
试想一下,如果一个分支的深度为1000,不压缩路径那么这个分支每个节点平均查找次数为500,压缩一次下次再查找就是1次。
学会路径压缩,你基本可以秒杀大部分并查集的题。
代码实现
并查集实现起来较为简单,直接贴代码!代码很久前写的,如果有纰漏还请指出。
-
import java.util.Scanner;
-
public class DisjointSet {
-
static int tree[]=new int[100000];//假设有500个值
-
public DisjointSet() {set(this.tree);}
-
public DisjointSet(int tree[])
-
{
-
this.tree=tree;
-
set(this.tree);
-
}
-
//初始化所有都是-1 有两个好处,这样他们指向-1说明是自己,
-
//第二,-1代表当前森林有-(-1)个
-
public void set(int a[])
-
{
-
int l=a.length;
-
for(int i=0;i<l;i++)
-
{
-
a[i]=-1;
-
}
-
}
-
public int search(int a)//返回头节点的数值
-
{
-
if(tree[a]>0)//说明是子节点
-
{
-
return tree[a]=search(tree[a]);//路径压缩
-
}
-
else
-
return a;
-
}
-
public int value(int a)//返回a所在树的大小(个数)
-
{
-
if(tree[a]>0)
-
{
-
return value(tree[a]);
-
}
-
else
-
return -tree[a];
-
}
-
public void union(int a,int b)//表示 a,b所在的树合并
-
{
-
int a1=search(a);//a根
-
int b1=search(b);//b根
-
if(a1==b1) {System.out.println(a+"和"+b+"已经在一棵树上");}
-
else {
-
if(tree[a1]<tree[b1])//这个是负数,为了简单减少计算,不在调用value函数
-
{
-
tree[a1]+=tree[b1];//个数相加 注意是负数相加
-
tree[b1]=a1; //b树成为a的子树,直接指向a;
-
}
-
else
-
{
-
tree[b1]+=tree[a1];//个数相加 注意是负数相加
-
tree[a1]=b1; //b树成为a的子树,直接指向a;
-
}
-
}
-
}
-
public static void main(String[] args)
-
{
-
DisjointSet d=new DisjointSet();
-
d.union(1,2);
-
d.union(3,4);
-
d.union(5,6);
-
d.union(1,6);
-
-
d.union(22,24);
-
d.union(3,26);
-
d.union(36,24);
-
System.out.println(d.search(6)); //头
-
System.out.println(d.value(6)); //大小
-
System.out.println(d.search(22)); //头
-
System.out.println(d.value(22)); //大小
-
}
-
}
结语
并查集属于简单但是很高效率的数据结构。在集合中经常会遇到。如果不采用并查集而传统暴力效率太低,而不被采纳。
另外,并查集还广泛用于迷宫游戏中,下面有机会可以介绍用并查集实现一个走迷宫小游戏。大家欢迎关注!
推荐阅读:
相互吹捧,共同进步,欢迎关注我的公众号:【bigsai】欢迎加个好友【q1315426911】交流,也可拉你进群交流学习,也可做个朋友圈点赞之交!如果感觉有收获还请点赞、在看、分享一波!
各位xdm希望能点个一键三连,小big在这里感激不尽
文章来源: bigsai.blog.csdn.net,作者:Big sai,版权归原作者所有,如需转载,请联系作者。
原文链接:bigsai.blog.csdn.net/article/details/116213435