1、走迷宫与回溯算法

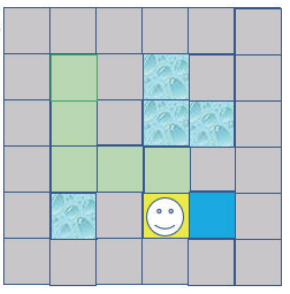
假设一个简单的迷宫图形如下图所示：

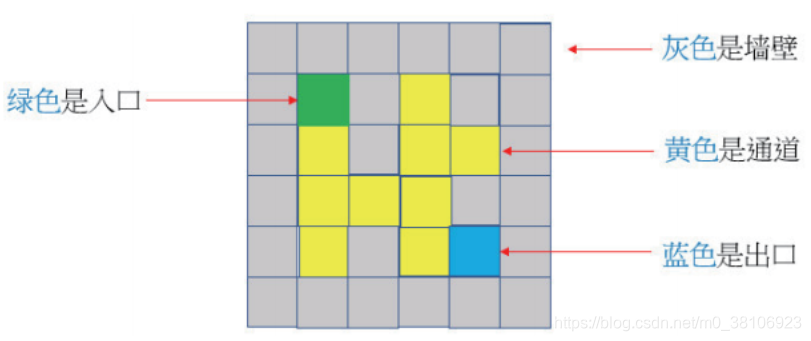
一个迷宫基本上由4种空格组成：


  
   
    
     
    
    
     
      入口：迷宫的入口，笔者上图用绿色表示。
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
     
      通道：迷宫的通道，笔者上图用黄色表示。
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
     
      墙壁：迷宫的墙壁，不可通行，笔者上图用灰色表示。
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
     
      出口：迷宫的出口，笔者上图用蓝色表示。

在走迷宫时，可以上、下、左、右行走，如下图所示：

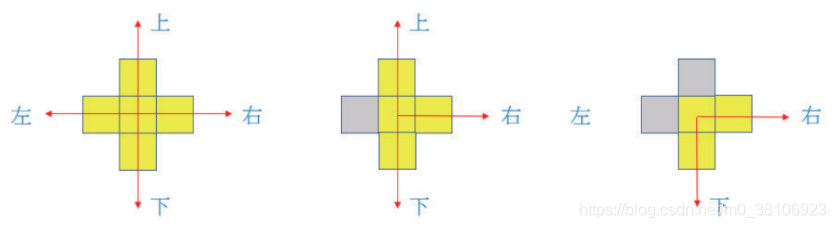
走迷宫时每次可以走一步，如果碰到墙壁不能穿越必须走其他方向。

第1步：假设目前位置在入口处，可以参考下图所示：

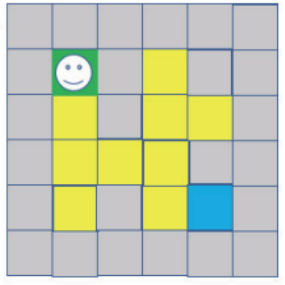
第2步：如果依照上、下、左、右原则，应该向上走，但是往上是墙壁，所以必须往下走，然后必须将走过的路标记，此例是用浅绿色标记，所以上述右图是在迷宫中的新位置，如下图所示：

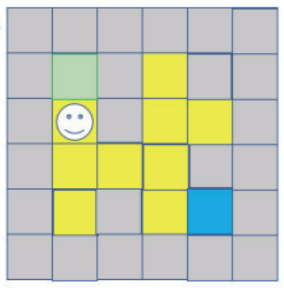
第3步：接下来可以发现往上是走过的路，所以只能往下发（依据上、下、左、右原则，先不考虑左、右是墙壁），下方左图是新的迷宫位置，如下图所示：

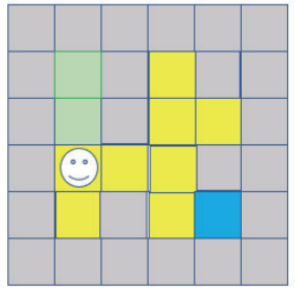
第4步：接下来可以发现往上是走过的路，所以只能往下（依据上、下、左、右原则，先不考虑左、右），下方右图是新的迷宫位置，如下图所示：

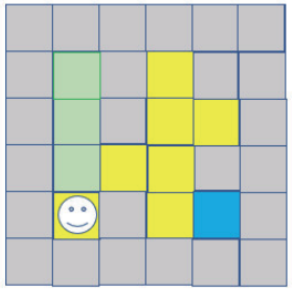
第5步：现在下、左、右皆是墙壁，所以回到前面走过的路，这一步就是回溯的关键，可参考下方左图，在此图中笔者将造成回溯的路另外标记，以防止再次造访，如下图所示：

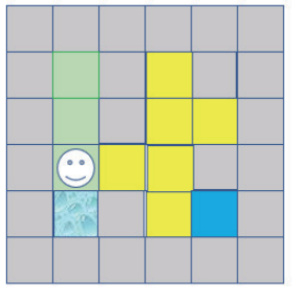
第6步：现在上、下皆是走过的路，左边是墙壁，所以往右走，如下图所示：

第7步：接下来上、下是墙壁，左边是走过的路，所以往右走，如下图所示：

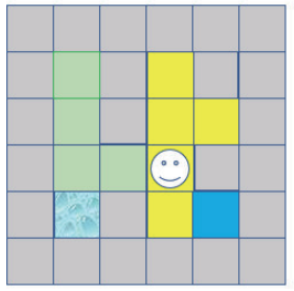
第8步：由于上方有路所以往上走，如下图所示：

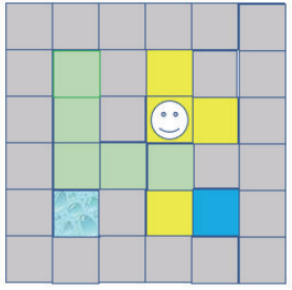
第9步：由于上方有路所以往上走，如下图所示：

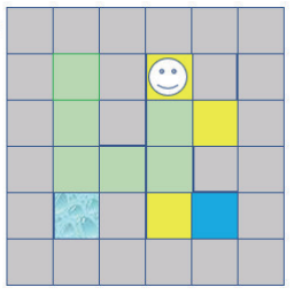
第10步：由于上、左、右皆是墙壁，所以回溯到前一个位置，如下图所示：

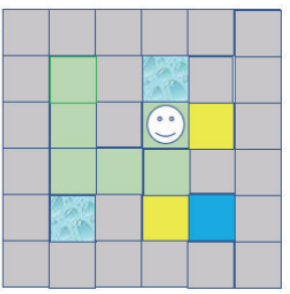
第11步：由于上、下是走过的路，左边是墙壁，所以往右走，如下图所示：

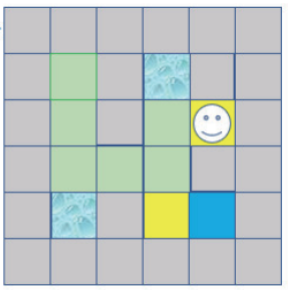
第12步：由于上、下、右是墙壁，所以回溯到先前位置，如下图所示：

第13步：由于左边是墙壁，所以回溯到先前走过的位置，如下图所示：

第14步：下方有通道，所以往下走，如下图所示：

第15步：上方是走过的位置，左方和下方是墙壁，所以往右走，如下图所示：

2、迷宫设计栈扮演的角色

上面介绍到，在第2步使用浅绿色标记走过的路，真实程序设计可以用栈存储走过的路。

第5步使用回溯算法，所谓的回溯就是走以前走过的路，因为是将走过的路使用栈(stack)存储，基于后进先出原则，可以pop出前一步路径，这也是回溯的重点。当走完第4步时，

迷宫与栈图形如下所示：

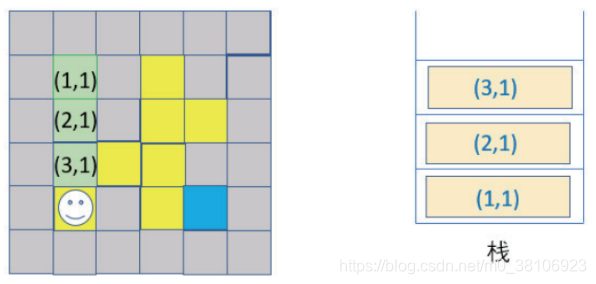
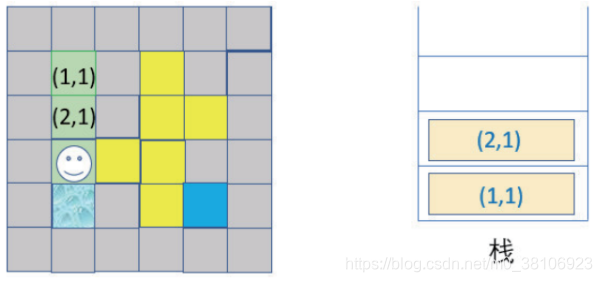
上述迷宫位置使用程序语言的(row，column)标记，所以第5步要使用回溯时，可以从栈pop出(3，1)坐标，回到(3，1)位置，结果如下所示所示：

3、Python实现走迷宫

使用Python设计走迷宫可以使用二维的列表，0代表通道、1代表墙壁，至于起点和终点也可以用0代表。

使用上述第一部分的迷宫实例，其中所经过的路径用2表示，经过会造成无路可走的路径用3表示。程序第41行前2个参数是迷宫的入口，后2个参数是迷宫的出口，实现代码如下所示：


  
   
    
     
    
    
     
      # ch11_1.py
     
    
   
    
     
    
    
     
      from pprint import pprint
     
    
   
    
     
    
    
     
      maze = [ # 迷宫地图
     
    
   
    
     
    
    
     
       [1, 1, 1, 1, 1, 1],
     
    
   
    
     
    
    
     
       [1, 0, 1, 0, 1, 1],
     
    
   
    
     
    
    
     
       [1, 0, 1, 0, 0, 1],
     
    
   
    
     
    
    
     
       [1, 0, 0, 0, 1, 1],
     
    
   
    
     
    
    
     
       [1, 0, 1, 0, 0, 1],
     
    
   
    
     
    
    
     
       [1, 1, 1, 1, 1, 1]
     
    
   
    
     
    
    
     
       ] 
     
    
   
    
     
    
    
     
      directions = [ # 使用列表设计走迷宫方向
     
    
   
    
     
    
    
      lambda x, y: (x-1, y), # 往上走
     
    
   
    
     
    
    
      lambda x, y: (x+1, y), # 往下走
     
    
   
    
     
    
    
      lambda x, y: (x, y-1), # 往左走
     
    
   
    
     
    
    
      lambda x, y: (x, y+1), # 往右走 
     
    
   
    
     
    
    
     
       ]
     
    
   
    
     
    
    
     
      def maze_solve(x, y, goal_x, goal_y):
     
    
   
    
     
    
    
      ''' 解迷宫程序 x, y是迷宫入口, goal_x, goal_y是迷宫出口'''
     
    
   
    
     
    
    
     
       maze[x][y] = 2
     
    
   
    
     
    
    
     
       stack = [] # 建立路径栈
     
    
   
    
     
    
    
     
       stack.append((x, y)) # 将路径push入栈
     
    
   
    
     
    
    
     
       print('迷宫开始')
     
    
   
    
     
    
    
      while (len(stack) > 0):
     
    
   
    
     
    
    
     
       cur = stack[-1] # 目前位置
     
    
   
    
     
    
    
      if cur[0] == goal_x and cur[1] == goal_y:
     
    
   
    
     
    
    
     
       print('抵达出口')
     
    
   
    
     
    
    
      return True # 抵达出口返回True 
     
    
   
    
     
    
    
      for dir in directions: # 依上, 下, 左, 右优先次序走此迷宫
     
    
   
    
     
    
    
     
       next = dir(cur[0], cur[1])
     
    
   
    
     
    
    
      if maze[next[0]][next[1]] == 0: # 如果是通道可以走
     
    
   
    
     
    
    
     
       stack.append(next)
     
    
   
    
     
    
    
     
       maze[next[0]][next[1]] = 2  # 用2标记走过的路
     
    
   
    
     
    
    
      break
     
    
   
    
     
    
    
      else: # 如果进入死路, 则回溯
     
    
   
    
     
    
    
     
       maze[cur[0]][cur[1]] = 3 # 标记死路
     
    
   
    
     
    
    
     
       stack.pop() # 回溯 
     
    
   
    
     
    
    
      else:
     
    
   
    
     
    
    
     
       print("没有路径")
     
    
   
    
     
    
    
      return False
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
     
      maze_solve(1, 1, 4, 4)
     
    
   
    
     
    
    
     
      pprint(maze) # 跳行显示元素

运行效果如下所示：

项目源码下载：用栈、回溯算法设计迷宫程序

本文来源：清华计算机学堂

文章来源: handsome-man.blog.csdn.net，作者：不脱发的程序猿，版权归原作者所有，如需转载，请联系作者。

原文链接：handsome-man.blog.csdn.net/article/details/109267933

（完）

目录

1、走迷宫与回溯算法

2、迷宫设计栈扮演的角色

3、Python实现走迷宫