前言
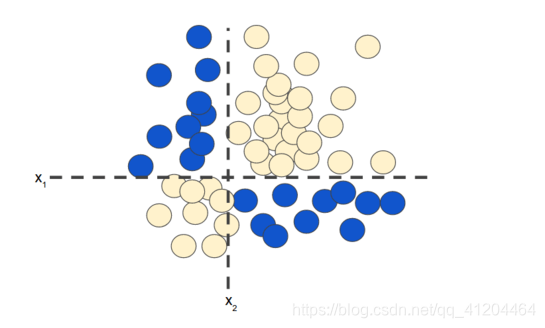
本文主要介绍神经网络。有些分类问题是属于非线性问题:
“非线性”意味着无法使用这样的形式: 的模型精准预测标签。即:“决策面”不是直线。
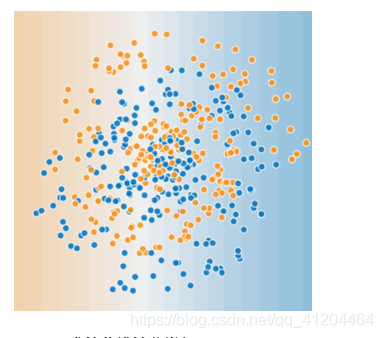
如果数据集如下所示(更难的非线性分类问题):
上图的数据集问题,无法使用线性模型解决。
非线性问题解决方法
或者可以考虑一个可行方法,对非线性问题进行建模——特征组合。
或者使用神经网络解决非线性问题,通常效果较好;它不一定始终比特征组合好,但它确实可以提供适用于很多情形的灵活代替方案。
单层神经网络
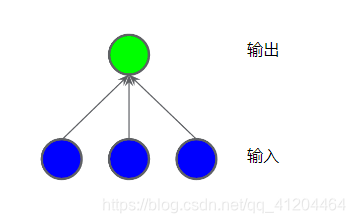
单层神经网络,其实也是一个线性模型,模型结构如下:
每个蓝色圆圈均表示一个输入特征,绿色圆圈表示各个输入的加权和。
这里明明有输出层、输出层,为什么叫单层神经网络呢?
通常,统计神经网络层数时,对有权重参数的层,才进行统计。输入层只负责特征数据输入,没有参数,所以不纳入统计层数的。
两层神经网络
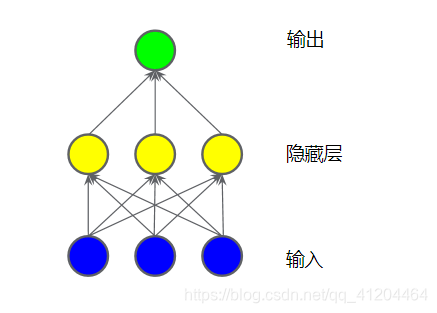
在输入层和输出层之间,添加多一层网络,其称为隐藏层。如下图所示:
隐藏层中的每个黄色节点均是,蓝色输入节点值的加权和。输出时黄色节点的加权和。
两层神经网络,其输出仍是其输入的线性组合。
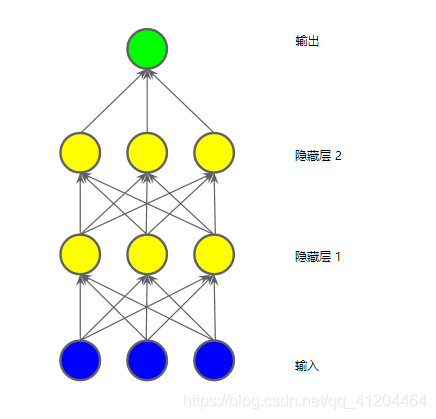
三层神经网络
由输出层、隐藏层1、隐藏层2、输出层组成;在输入层和输出层之间的都可以称为隐藏层。:
此模型仍是线性的;当将输出表示为输入的函数并进行简化时,只是获得输入的另一个加权和而已。
该加权和无法对非线性问题,进行有效建模。
激活函数
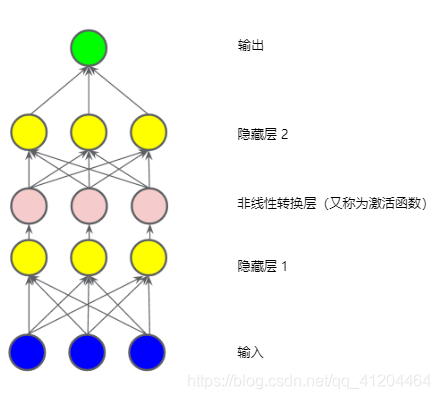
要对非线性问题进行建模,我们可以直接引入非线性函数。我们可以使用非线性函数将每个隐藏节点享管道一样连接起来。
在下图所示的模型中,在隐藏层1中各个节点的只传递到一下层,进行加权求和之前;我们采用一个非线性函数对其进行了转换。这种非线性函数成为激活函数。
包含激活函数的三层模型:
现在,我们已经添加了激活函数,如果添加层,将会产生更多影响。通过在非线性上堆叠非线性,我们能够对输入和预测输出之间极其复杂的关系进行建模。
每一层均可通过原始输入有效学习更复杂、更高级别的函数。
常见激活函数
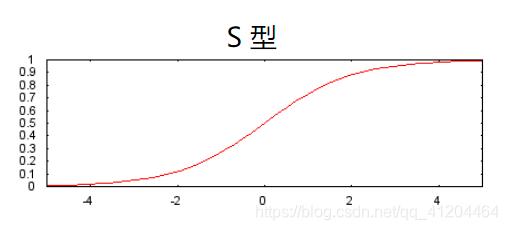
1、S型激活函数,将加权和转换为介于0和1之间的值。
曲线图如下:
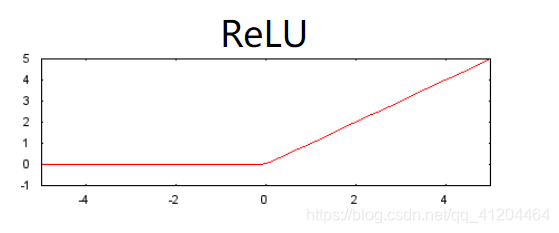
2、修正线性单元激光函数,简称ReLU,相对于S型函数等平滑函数,它的效果通常要好一点,同时还非常易于计算。
ReLU的优势在于它基于实证发现,拥有更实用的响应范围。S型函数的响应性在两端相对较快地减少。ReLU激活函数如下所示:
实际上,所有数学函数均可作为激光函数。假设表示我们的激活函数(ReLuck、S型函数等等)。因此,网络中节点的值由以下公式指定:
总结
现在,我们的模型拥有了人们通常所说的“神经网络”的所有标准组件:
- 一组节点,类似于神经元,位于层中。
- 一组权重,表示每个神经网络层与下方的层之间的关系。下方的层可能是另一个神经网络层,也可能是其他类型的层。
- 一组偏差,每个节点一个偏差。
- 一个激活函数,对层中每个节点的输出进行转换。不同的层可能拥有不同的激光函数。
参考:https://developers.google.cn/machine-learning/crash-course/introduction-to-neural-networks/anatomy