一、题目内容
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
- 类型 1:只能由 Alice 遍历。
- 类型 2:只能由 Bob 遍历。
- 类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:
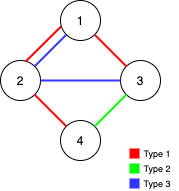
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出:2
解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
示例 2:

输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出:0
解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3:

输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出:-1
解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
提示:
1 <= n <= 10^5
1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
edges[i].length == 3
1 <= edges[i][0] <= 3
1 <= edges[i][1] < edges[i][2] <= n
所有元组 (typei, ui, vi) 互不相同
二、解题思路
维护三种线段的连通关系,线段3一般要保留,毕竟是公用的。
具体思路看代码注释。
三、代码
-
class Solution:
-
def maxNumEdgesToRemove(self, n: int, edges: list) -> int:
-
uf1 = UnionFind(n)
-
uf2 = UnionFind(n)
-
uf3 = UnionFind(n)
-
-
count1 = 0 # 线段1的个数
-
count2 = 0 # 线段2的个数
-
count3 = 0 # 线段3的个数
-
redundant_count3 = 0 # 线段3冗余的个数
-
-
for i in range(len(edges)):
-
edge_type = edges[i][0] # 线段种类
-
st = edges[i][1] - 1
-
ed = edges[i][2] - 1
-
-
# 记录每种线段的个数
-
if edge_type == 1:
-
count1 += 1
-
elif edge_type == 2:
-
count2 += 1
-
elif edge_type == 3:
-
count3 += 1
-
else:
-
raise ValueError
-
-
# 每种线段进行连通
-
if edge_type == 1 or edge_type == 3:
-
uf1.Union(st, ed)
-
-
if edge_type == 2 or edge_type == 3:
-
uf2.Union(st, ed)
-
-
if edge_type == 3:
-
if not uf3.isConnected(st, ed):
-
uf3.Union(st, ed)
-
else:
-
# 已经连通说明冗余
-
redundant_count3 += 1
-
# 线段3直接连通了所有点
-
if uf3.getCount() == 1:
-
return count1 + count2 + redundant_count3 # 删除的边可以是线段1+线段2+线段3冗余的个数
-
# 线段1和线段2同时连通, 那么都可以走的路不需要删除,也就是线段3不需要删除,但是要删除线段3的冗余
-
if uf1.getCount() == 1 and uf2.getCount() == 1:
-
return count1 - (uf3.getCount() - 1) + \
-
count2 - (uf3.getCount() - 1) + redundant_count3
-
-
return -1
-
-
-
class UnionFind:
-
def __init__(self, n):
-
self.count = n
-
self.root = [0 for _ in range(n)]
-
self.size = [0 for _ in range(n)]
-
-
for i in range(n):
-
self.root[i] = i
-
self.size[i] = i
-
-
def find(self, x):
-
if x != self.root[x]:
-
self.root[x] = self.find(self.root[x])
-
return self.root[x]
-
else:
-
return x
-
-
def isConnected(self, x, y):
-
return self.find(x) == self.find(y)
-
-
def getCount(self):
-
return self.count
-
-
def Union(self, x, y):
-
# 查找x和y的根/父节点
-
rx = self.find(x)
-
ry = self.find(y)
-
-
# 根/父节点相同, 说明已经连通了
-
if rx == ry:
-
return # 直接返回
-
if self.size[rx] < self.size[ry]:
-
self.root[rx] = ry
-
self.size[ry] += self.size[rx]
-
else:
-
self.root[ry] = rx
-
self.size[rx] += self.size[ry]
-
self.count -= 1
-
-
-
if __name__ == '__main__':
-
s = Solution()
-
n = 4
-
edges = [[3, 1, 2],
-
[3, 2, 3],
-
[1, 1, 3],
-
[1, 2, 4],
-
[1, 1, 2],
-
[2, 3, 4]]
-
-
ans = s.maxNumEdgesToRemove(n, edges)
-
print(ans)
-
文章来源: nickhuang1996.blog.csdn.net,作者:悲恋花丶无心之人,版权归原作者所有,如需转载,请联系作者。
原文链接:nickhuang1996.blog.csdn.net/article/details/113242638