机器学习11-正则化L1（稀疏性）

前言

$L_{1}$ 正则化，也称稀疏性正则化。

创建特征组合会导致包含更多维度；由于使用此类高纬度特征矢量，因此模型可能会非常庞大，并且需要大量的RAM。

在高纬度稀疏矢量中，最好尽可能使权重正好降至0。正好为0的权重基本会使相应特征从模型中移除。将特征设为0可节省RAM空间，且可以减少模型中的噪点。

L1正则化（L1 regularization），一种正则化，根据权重的绝对值的总和来惩罚权重。在以来稀疏特征的模型中，L1正则化有助于使不相关或几乎不相关的特征的权重正好为0，从而将这些特征从模型中移除。与L2正则化相对。

对比： $L_{2}$ 正则化可以使权重变小，但是并不能使它们正好为0.0。

$L_{1}$ 和 $L_{2}$ 采用不同的方式降低权重：

因此， $L_{1}$ 和 $L_{2}$ 具有不同的导数：

$L_{1}$ 导数的作用理解为：每次从权重中减去一个常数。不过，由于减去的是绝对值， $L_{1}$ 在0处具有不连续性，这会导致与0相交的减法结果变为0。例如，如果减法使权重从+0.1变为-0.2， $L_{1}$ 便会将权重设为0。就这样， $L_{1}$ 使权重变为0了。

$L_{2}$ 的导数作用理解为：每次移除权重的x%。对于任意数字，即使按每次减去x%的幅度执行数十亿次减法计算，最后得出的值也绝不会正好为0。即， $L_{2}$ 通常不会使权重变为0。

小结： $L_{1}$ 正则化，减少所有权重的绝对值，对宽度模型非常有效。

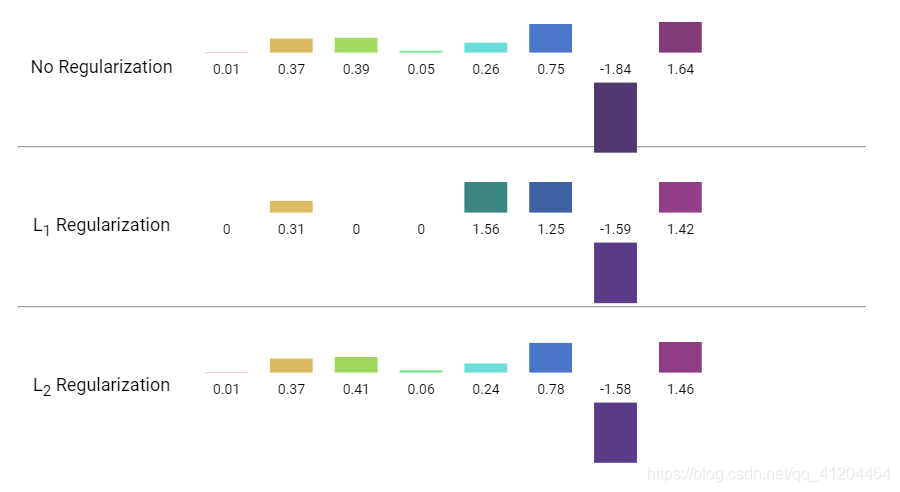
下面是比较 L1 和 L2 正则化对权重网络的影响：

能看到L1正则化会把很小的权重变为0；

L1正则化（L1 regularization），一种正则化，根据权重的绝对值的总和，来惩罚权重。在以来稀疏特征的模型中，L1正则化有助于使不相关或几乎不相关的特征的权重正好为0，从而将这些特征从模型中移除。与L2正则化相对。

L2正则化（L2 regularization），一种正则化，根据权重的平方和，来惩罚权重。L2正则化有助于使离群值（具有较大正值或较小负责）权重接近于0，但又不正好为0。在线性模型中，L2正则化始终可以进行泛化。

（完）