[LeetCode] Binary Tree Level Order Traversal 二叉树层次遍历(DFS

目录：
1.Binary Tree Level Order Traversal - 二叉树层次遍历 BFS
2.Binary Tree Level Order Traversal II - 二叉树层次遍历从低往高输出 BFS
3.Maximum Depth of Binary Tree - 求二叉树的深度 DFS
4.Balanced Binary Tree - 判断平衡二叉树 DFS
5.Path Sum - 二叉树路径求和判断DFS

题目概述：
Given a binary tree, return the level order traversal of its nodes' values. (ie, from left to right, level by level).
For example:
Given binary tree {3,9,20,#,#,15,7},

return its level order traversal as:

[
  [3],
  [9,20],
  [15,7]
]

Here's an example:

The above binary tree is serialized as "{1,2,3,#,#,4,#,#,5}".

题目分析：
本题考查的就是二叉树的层次遍历，需要注意的是二叉树用数组的表示方法，二叉树的每层是从左到右存入数组的。方法包括：
1.层次遍历。二维数组存储数字和深度，输出二维数组即可，过于复杂。
2.通过队列BFS广度优先搜索。
3.通过DFS深度优先搜索实现。

我的代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    //二叉树层次遍历 通过队列BFS广度优先搜索
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        queue<TreeNode*>q;            
        vector<int> level;       //每层结果
        int size,i;
        TreeNode* p;
        
        if(root==NULL) return result;
        q.push(root);            //入队
        while(!q.empty()) {
            //队列中有几个元素就依次遍历每个元素的左右结点
            level.clear();
            size=q.size();
            for(i=0; i<size; i++) {
                p=q.front();     //队首元素值赋给p
                q.pop();         //出队
                level.push_back(p->val);
                if(p->left) {    //依次压入左右结点元素
                    q.push(p->left);
                }
                if(p->right) {
                    q.push(p->right);
                }
            }
            result.push_back(level);   //添加每层数据
        }
        return result;
    }
};

代码详解：
该题目你如果采用C语言二维数组过于复杂，故采用C++的容器vector实现。同时BFS广度优先搜索采用队列queue实现，常见方法如下(参考地址)：
1.栈操作

#include<stack>         头文件
stack<int> s            定义栈
s.empty()               如果栈为空返回true，否则返回false  
s.size()                返回栈中元素的个数  
s.pop()                 删除栈顶元素但不返回其值  
s.top()                 返回栈顶的元素，但不删除该元素  
s.push()                在栈顶压入新元素

2.队列操作

#include<queue>         头文件
queue<int> q            定义队列
q.empty()               如果队列为空返回true，否则返回false  
q.size()                返回队列中元素的个数  
q.pop()                 删除队列首元素但不返回其值  
q.front()               返回队首元素的值，但不删除该元素  
q.push()                在队尾压入新元素  
q.back()                返回队列尾元素的值，但不删除该元素

3.二叉树层次遍历如何使用队列
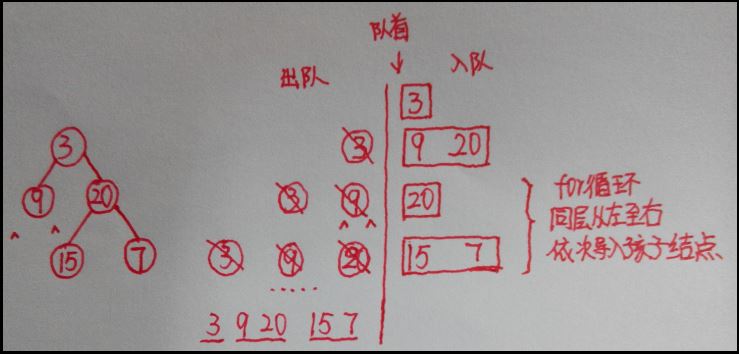
由于二叉树是从左至右进行输入，故层次遍历通过队列存储每层的结点，它存储的顺序也是前一个结点的左孩子结点、右孩子结点，依次顺序进出队列。

DFS代码参考地址：LeetCode Binary Tree Level Order Traversal

其他题目：
Binary Tree Level Order Traversal II
层次遍历从低往root结点输出，如 Given binary tree {3,9,20,#,#,15,7},

return its level order traversal as:

[
  [15,7],
  [9,20],
  [3]
]

最简单方法通过层次遍历BFS调用队列后逆序倒置vector容器即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> result;
        vector<int> level;
        queue<TreeNode*> q;
        
        if(root==NULL)
            return result;
        q.push(root);
        while(!q.empty()) {
            //层次遍历
            level.clear();
            int size=q.size();
            for(int i=0; i<size; i++) { //注意:不能i<q.size() 当入队时它会变换
                TreeNode* p=q.front();
                q.pop();
                level.push_back(p->val);
                if(p->left)
                    q.push(p->left);
                if(p->right)
                    q.push(p->right);
            }
            //每层结果存入容器
            result.push_back(level);
        }
        /*
         * 逆序输出 倒置容器调用函数
         * reverse(result.begin(),result.end());
         * return result;
         */
        vector<vector<int>>::iterator iter;  //迭代器
        vector<vector<int>> res;
        for(iter=result.end()-1; iter!=result.begin()-1; iter--)
        {
            level.clear();
            for(int i=0; i<(*iter).size(); i++) //复制每层内容
            {
                level.push_back((*iter)[i]);
            }
            res.push_back(level);
        }
        return res;
    }
};

PS：如果是每层的也要逆序的话，就把left 和right 入队的顺序调换一下。另一种遍历方法参考：http://www.cnblogs.com/ganganloveu/p/3843470.html

Maximum Depth of Binary Tree - 求二叉树的深度
常见方法通过BFS层次遍历计算二叉树层数及深度或通过DFS计算二叉树从root到leaf结点最长路径及深度，在采用BSF代码中可通过前面代码进行修改，但错误：
[0,2,4,1,null,3,-1,5,1,null,6,null,8] output=5 Excepted=4
故采用DFS进行深度递归搜索。代码如下：

int maxDepth(struct TreeNode* root) {
    if(root == NULL) return 0;
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);
    return (left >= right ? left : right) + 1;
}

BFS代码参考：http://blog.csdn.net/sunbaigui/article/details/8980887

Balanced Binary Tree - 判断平衡二叉树
平衡二叉树是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。参考前面的计算深度方法完成。

 int DFS(struct TreeNode* p) {
    if(p==NULL)
        return 0;
    int left=DFS(p->left);
    int right=DFS(p->right);
    return (left>=right?left:right)+1;
 }
//递归判断左右子树结点是否符合平衡二叉树
bool isBalancedNode(struct TreeNode* L,struct TreeNode* R) {
    if(!L&&!R) 
        return true;
    //自定义DFS函数计算结点的深度
    int left=DFS(L);
    int right=DFS(R);
    //平衡二叉树左右结点深度相差0或1
    if(abs(left-right)>1) 
        return false;
    else if(L&&R) //必须存在 否则会报错RE [1,2]时R->left不存在
        return isBalancedNode(L->left,L->right) && isBalancedNode(R->left,R->right);
}
bool isBalanced(struct TreeNode* root) {
    if(root==NULL)
        return true;
    if(root&&!root->left&&!root->right)
        return true;
    else 
        return isBalancedNode(root->left,root->right);
}

另一种方法参考地址，也可通过后序遍历实现。

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool checkBalance(TreeNode *node, int &dep)
    {
        if (node == NULL)
        {
            dep = 0;
            return true;
        }
        
        int leftDep, rightDep;
        bool leftBalance = checkBalance(node->left, leftDep);
        bool rightBalance = checkBalance(node->right, rightDep);
        
        dep = max(leftDep, rightDep)+1;
        
        return leftBalance && rightBalance && (abs(rightDep - leftDep) <= 1);
    }
    
    bool isBalanced(TreeNode *root) {
        int dep;
        return checkBalance(root, dep);
    }
};

Path Sum - 二叉树路径求和判断

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.For example:
Given the below binary tree and sum = 22,

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

该题主要考察DFS或BFS计算root到leaf结点路径求和是否存在一条与sum相等的path。我采用DFS结合计算二叉树深度完成，最初打算自定义isNode(*root,num)函数判断，后来直接通过判断每个结点是否是leaf且值为sum-前面结点。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

//思路：通过DFS计算root-to-leaf的结果
bool hasPathSum(struct TreeNode* root, int sum) {
    if(root==NULL)
        return false;
    else if(root&&!root->left&&!root->right&&root->val==sum)  //仅root结点
        return true;
    else if(root&&!root->left&&!root->right&&root->val!=sum)
        return false;
    else  //包括子结点
        return hasPathSum(root->left,(sum - root->val)) ||
            hasPathSum(root->right,(sum - root->val));
}

2015年的文章，希望您喜欢。

原文地址：https://blog.csdn.net/Eastmount/article/details/48359685

(By:Eastmount 2021-7-31 夜于武汉)

（完）