前言
许多问题需要将概率估算值作为输出。逻辑回归是一种极其高效的概率计算机制。
计算并返回概率的方式
- 按原样
- 转换成二元类别
按原样使用概率;假设我们创建一个逻辑回归模型来预测狗在半夜发出叫声的概率。我们将此概率称为:
如果逻辑回归模型预测的值为0.05,那么一年内(365天),主人被狗惊醒约18次:
即:18 = 0.05 * 365
转换为二元类别
在很多情况下,将逻辑回归输出映射到二元分类问题的解决方案,该二元分类问题的目标是正确预测两个可能的标签中的一个。
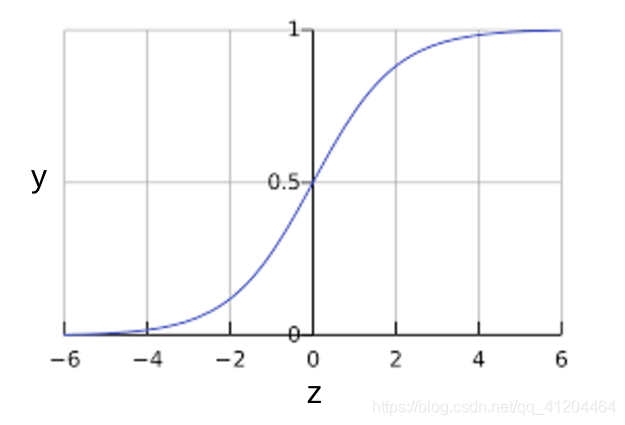
S形函数
逻辑回归模型如何确保输出值始终落在0和1之间呢?S型函数生成的输出值正好具有这些特征,其定义如下:
S型函数会产生以下曲线:
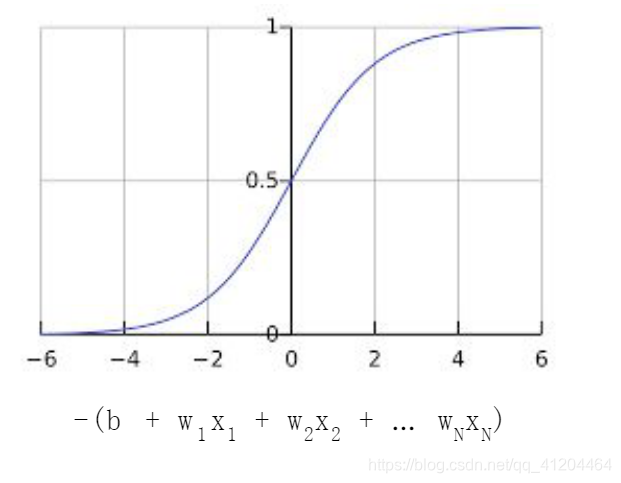
如果z表示使用逻辑回归训练的模型的线性层的输出,则S型函数会生成一个介于0和1之间的值(概率)。用数学方法表示为:
其中:
- 是逻辑回归模型针对特定样本的输出。
- z是;w是该模型学习的权重,b是偏差。x是指特征样本的特征值。
请注意,z也称为对数几率,因为S型函数的反函数表明:z可定义为标签“1”的概率除以标签“0”的概率,得出的值的对数:
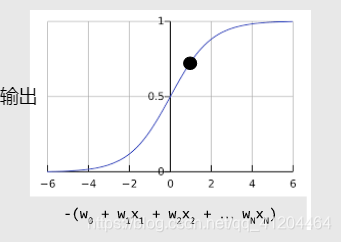
以下是具有机器学习标签的S型函数:
逻辑回归推断计算
假设我们的逻辑回归模型具有学习了下列偏差和权重的三个特征:
- b = 1
- w1 = 2
- w2 = -1
- w3 = 5
进一步假设给定样本具有以下特征:
- x1 = 0
- x2 = 10
- x3 =2
因此,对数几率:
代入公式计算得:(1)+(2)(0)+(-1)(10)+(5)(2)=1
因此,此特定样本的逻辑回归预测值将是0.731:
概率输出为0,731,即73.1%的概率:
逻辑回归的损失函数
线性回归的损失函数是平方损失。逻辑回归的损失函数是对数损失函数,定义如下:
其中:
- 是包含很多有标签样本(x,y)的数据集。
- y是有标签样本的标签。由于这是逻辑回归,因此y的每个值都必须使0或1.
- 是对于特征集x的预测值(介于0和1之间)。
对数损失函数的方程式,是似然函数的负对数。
逻辑回归中的正则化
正则化在逻辑回归建模中极其重要。如果没有正则化,逻辑回归的逐渐性会不断促使损失在搞维度空间内达到0.因此,大多数逻辑回归模型会使用一下两个策略之一来降低模型复杂性:
- 正则化。
- 早停法,即:限制训练步数或学习率。
假设向每个样本分配一个唯一ID,且将每个ID映射到其自己的特征。如果未指定正则化函数,模型会变得完成过拟合。
这是因为模型会尝试促使所有样本的始终损失达不到0,从而使每个特征的权重接近正无穷或负无穷。当大量罕见的特征组合的高纬度数据就会出现这种情况。正则化或早停法可以防止此类问题。
小结
逻辑回归模型生成概率。
对数损失函数使逻辑回归的损失函数。
逻辑回归被很多从业者广发使用。
参考:https://developers.google.cn/machine-learning/crash-course/logistic-regression/model-training