因为被美团的大佬翻牌子了,所以内推直接免笔试进面试,恰巧今天遇到同学们答美团的笔试题,热爱OJ的我就参与了一发,战果还不错,2道题都轻松AC了。
接下来就和大家分享一下我的做题思路和代码,我觉得第一题还有改进的地方,希望大家不吝赐教,我也今晚好好想想有没有更优秀的解法。
首先是第一题:
序列中任意个连续的元素组成的子序列称为该序列的子串。
现在给你一个序列P和一个整数K,询问元素和是K的倍数的子串的最大长度。
样例输入:
[1,2,3,4,5],整数K,满足条件的子串是{5},{2,3},{1,2,3,4},{1,2,3,4,5}。
那么答案就是5。如果这样的子串不存在,就输出0.
这道题和今年蓝桥杯上面的一道题很想(虽然我也没参加,只是自己随便做了做它的题)。适用动态规划,维护一个dp矩阵,每个元素是前面元素和%K的结果,注意,我们计算下一个元素时,只需要根据递推公式: dp[i] = (dp[i-1]+arr[i])%K;即可。比如[1,2,3,4,5]就会得到[1,3,1,0,0]。
这时候我们再根据这个dp矩阵来计算最大长度,dp矩阵中元素一定是0,1,...K-1.
先看0.为0就代表前面的元素和正好是K的倍数,那么我们寻找数组中最后一个0的位置,就是dp[i]=0的最长子串长度-1.
然后看1,我们找dp矩阵中第一1的位置j和最后一个1之间的位置k的差,这个差值就是dp[i]=1的最长子串长度。相当于前k项和-前j项和正好是K的倍数。
...
依次类推到K-1,每次都维护最长距离max。最终输出。
同时加入arr.length==0的判断。
-
package com.nowcoder.java;
-
-
public class Meituan01 {
-
public static void main(String[] args) {
-
int[] arr={1,2,3};
-
int K = 5;
-
System.out.println(cal(arr,K));
-
}
-
-
public static int cal(int[] arr,int K){
-
if(arr.length==0)
-
return 0;
-
int max=0;
-
int[] dp = new int[arr.length];
-
dp[0] = arr[0]%K;
-
for(int i=1;i<dp.length;i++){
-
dp[i]=(dp[i-1]+arr[i])%K;
-
}
-
-
for(int i=0;i<dp.length;i++){
-
if(dp[i]==0)
-
max=i+1;
-
}
-
for(int i=1;i<K;i++){
-
int pre = 0;
-
int back = dp.length-1;
-
while(dp[pre]!=i && pre<back)
-
pre++;
-
while(dp[back]!=i && back>pre)
-
back--;
-
int len=back-pre;
-
if(len>max)
-
max=len;
-
}
-
return max;
-
}
-
}
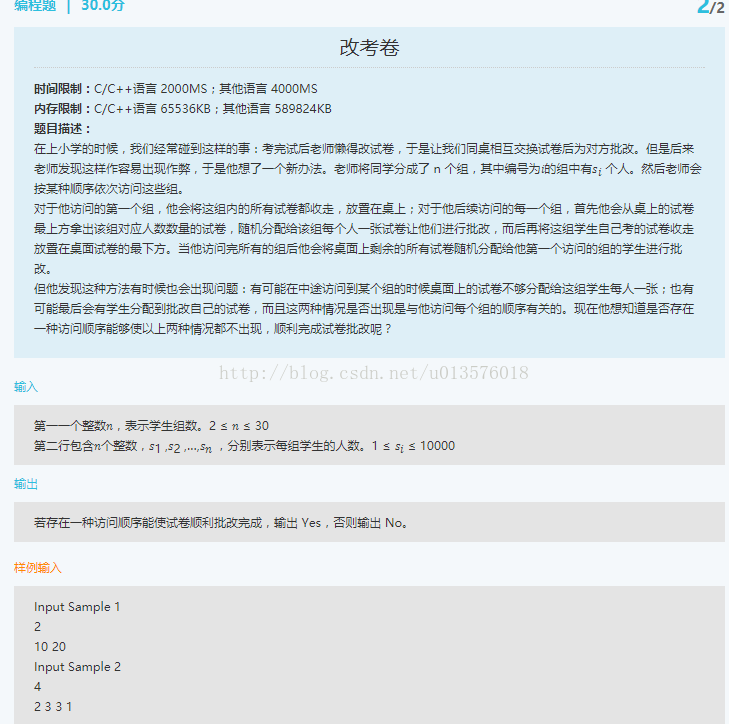
第二题:
太长了我直接贴图。
这道题乍看很难,其实道理只有一个!
那就是:最大的那一个组的人数一定要比其余组的和大于等于即可!
-
package com.nowcoder.java;
-
-
import java.util.Arrays;
-
-
public class Meituan02 {
-
public static void main(String[] args) {
-
int N=2;
-
int[] arr = new int[]{10,10,20};
-
System.out.println(check(arr,N));
-
}
-
public static boolean check(int[] arr,int N){
-
if(N<=1)
-
return false;
-
Arrays.sort(arr);
-
int sum = 0;
-
for(int i=0;i<N-1;i++){
-
sum+=arr[i];
-
}
-
if(sum>=arr[N-1])
-
return true;
-
else{
-
return false;
-
}
-
}
-
}
代码如上,
以上
文章来源: zclhit.blog.csdn.net,作者:zclhit_,版权归原作者所有,如需转载,请联系作者。
原文链接:zclhit.blog.csdn.net/article/details/77753327