LeetCode 32最长有效括号(困难)

维护不易，还请点个赞赞，如果想加入还请关注公众号bigsai回复进群加入打卡。

题目描述

给定一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

输入: “(()”
输出: 2
解释: 最长有效括号子串为 “()”

示例 2:

输入: “)()())”
输出: 4
解释: 最长有效括号子串为 “()()”

分析
再看这题之前，咱们回顾一下前面刷过的题。力扣20有效的括号
在这里插入图片描述

分析

这种题核心思想就是使用栈模拟。本题的话更简单一点因为只有(和 )两种括号，只有两个东西的话很多时候可以省略很多内容。在使用暴力的时候就可以循环每次找到最长的有效括号。而括号匹配的时候可以直接终止的情况是当前多个)右括号。例如())(到第三个不可能和前面相连，而如果来(只需要期待后面能够来)。一个)可以和一个(组成一对，消除栈中的一个(。

当然，在具体的实现上，我们用数组模拟栈，实现代码为：

public  int longestValidParentheses(String s) {
	char str[]=s.toCharArray();//字符数组
	int max=0;
	for(int i=0;i<str.length-1;i++)
	{
		int index=-1;
		if(max>=str.length-i) break;
		for(int j=i;j<str.length;j++)
		{ if(str[j]=='(') index++; else { if(index<0) { i=j; break; } else { index--; } } if(index==-1&&(j-i+1>max)) { max=j-i+1; }
		}
	}	
	return max; }

尽管有一些地方有优化空间，比如剪枝把各种不可能的给剪掉，但整个算法还是太复杂，算法的复杂度为O(n2).并且只击败5%的人，所以在这方面宣告算法宣告失败：
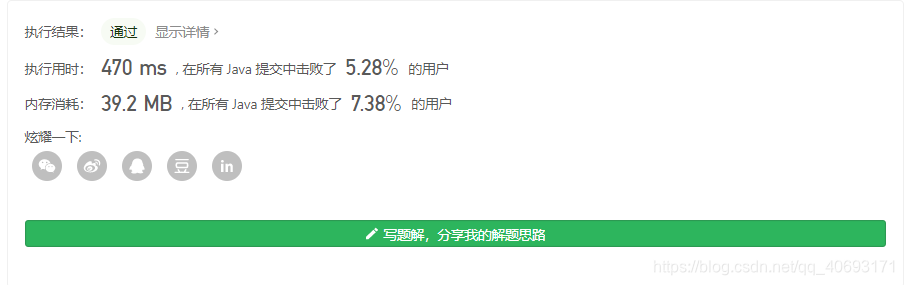
在这里插入图片描述

其实这个暴力是昨晚睡觉前过的，因为我看到困难级别我在刷的时候用暴力过了好歹我也是过了，过了之后上床之后我就在想怎么去优化这道题。

在今天早上的时候用笔画了画想了想成功攻破该题(看不懂不要紧，下面给你慢慢讲)：
在这里插入图片描述

如何将这道题从一个O(n2)的时间复杂度优化到O(n)？很容易，我们需要注意他的过程。我们先随便看几个可能的最大情况。

( ) ) ( ) ( ( ) ( ) ) 最大为后面部分
( ) ( ) ( ( ( ) 最大为前面部分
( ( ( ( ( ( ) ( ) ( ) ( ) 最大为后面部分

对于这么一次获取你会发现不同括号会有些区别：
(：左括号一旦出现那么他就期待一个)进行匹配，但它的后面可能有)并且在这中间有很多其他括号对。
):右扩号有两种情况：

一种是当前已经超过左括号前面已经不可能连续了。例如( ) ) ( )第三个括号出现已经使得整个串串不可能连续，最大要么在其左面，要么再其右面。你可以理解其为一种清零初始机制。
另一种情况)就是目标栈中存在(可与其进行匹配。匹配之后要叠加到消除后平级的数量上，并且判断是否是最大值。(下面会解释)

在具体实现的思路上，就是使用一个int数组标记当前层级(栈深)有正确的括号数量。模拟一次栈行为从左向右，遇到)太多(当前栈中不存在(进行匹配)就将数据清零重新开始。这样一直到最后。你可以把它看成台接，遇到(就上一个台阶并清零该新台阶，遇到)就下一个台阶并且把数量加到下降后的台阶上。具体可以看下面图片模拟呃过程：
( ) ( ( ) ( ) ( ( ) ) )

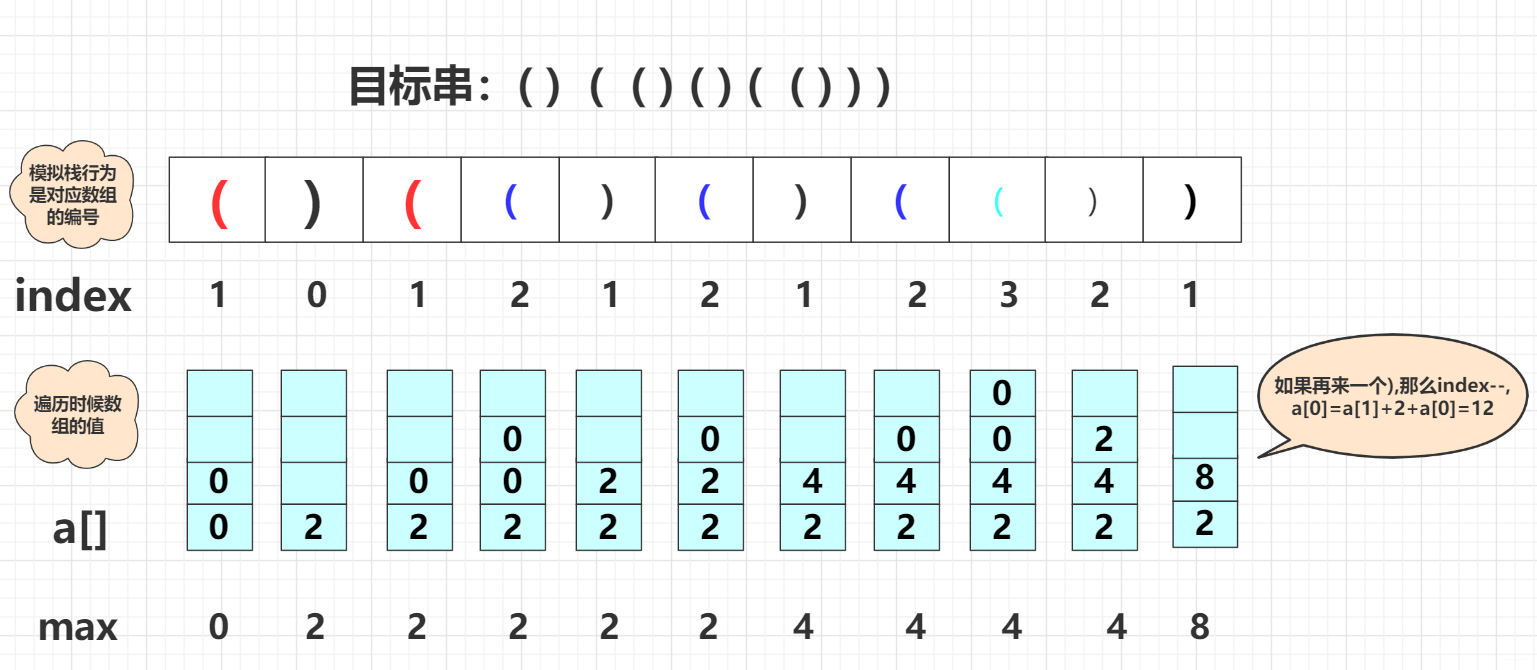
在这里插入图片描述

仔细看看这张图，具体实现代码为：

 public static int longestValidParentheses(String s) {
		int max=0; int value[]=new int[s.length()+1];
		int index=0;
		for(int i=0;i<s.length();i++)
		{ if(s.charAt(i)=='(') { index++; value[index]=0; } else {//")" if(index==0) { value[0]=0; } else { value[index-1]+=value[index--]+2;//叠加 if(value[index]>max)//更新 max=value[index]; } }
		}
		return max; }

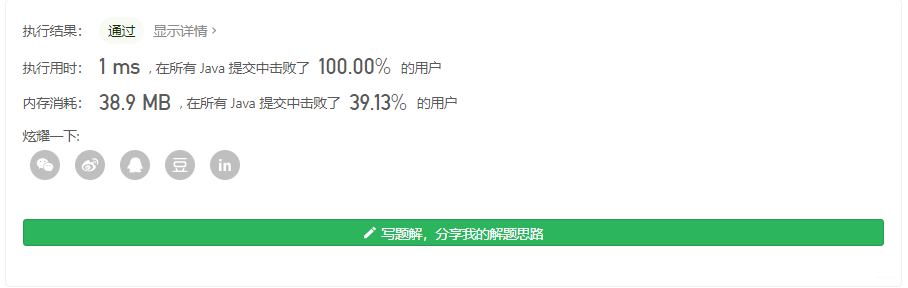
在这里插入图片描述
好啦，这个O(n)的复杂度还行，至于其他解法也没研究有空可以看看。这次打卡就结束啦，如果有兴趣的欢迎关注公众号bigsai 回复进群，加入打卡！一起刷题。

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/108810158

（完）