前言
梯度矢量具有方向和大小;梯度下降算法用梯度乘以一个称为学习率(有时也称为步长)的标量,以确定下一个点的位置。
例如,如果梯度大小为2.5,学习率为0.01,则梯度下降算法会选择距离前一个点0.025的位置作为下一个点。
学习率
超参数是编程人员在机器学习算法中用于调整的旋钮。大多数机器学习编程人员会花费相当多的时间来调整学习率。
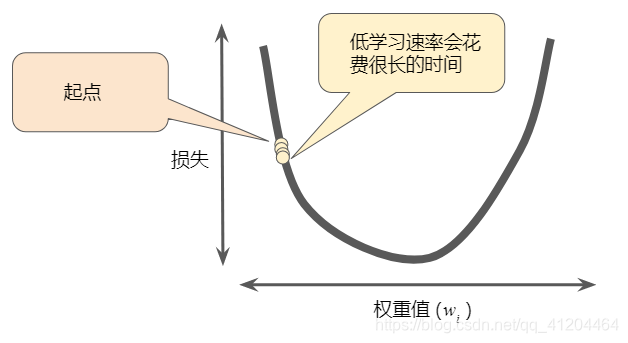
如果选择的学习率过小,就会花费太长的学习时间:
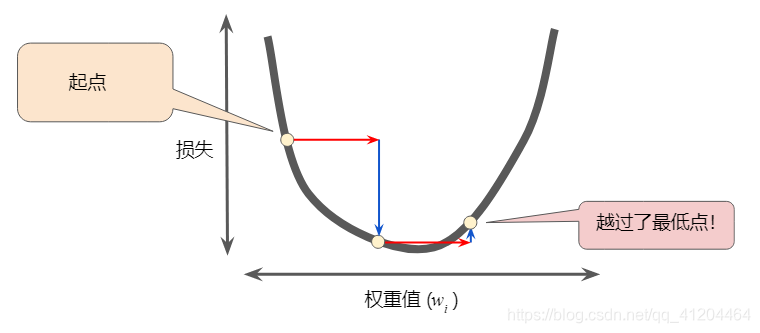
如果选择的学习率过大,下一个点将永远在U形曲线的底部随意弹跳,无法找到全局最低点:
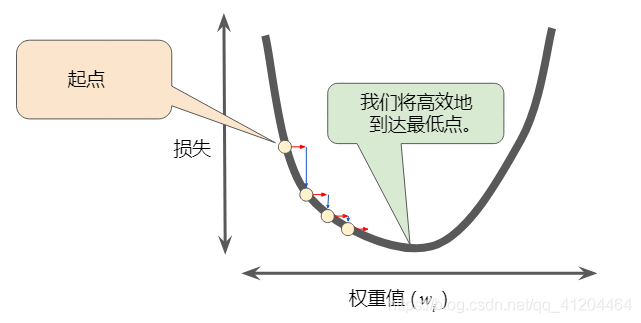
如果选择的学习率恰恰好:
选择学习率
学习率与损失函数的平坦程度相关。如果知道损失函数的梯度较小,则可以尝试更大的学习率,以补偿较小的梯度并获得更大的步长。
一维空间中的理想学习率是,对的二阶导数的倒数。
二维或多维空间中的理想学习率是 Hessian matrix(由二阶偏导数组成的矩阵)的倒数。
广义凸函数的情况则更为复杂。
详细的Hessian matrix参考维基百科: https://en.wikipedia.org/wiki/Hessian_matrix
关键词
参数(parameter),机器学习系统自行训练的模型变量。例如,权重。它们的值是机器学习系统通过连续的训练迭代逐渐学习到的;与超参数相对。
超参数(hyperparameter),在模型训练的连续过程中,需要人工指定和调整的;例如学习率;与参数相对。
学习率(learning rate),在训练模型时用于梯度下降的一个标量。在每次迭代期间,梯度下降法都会将学习速率与梯度相乘;得出的乘积称为梯度步长。
参考:https://developers.google.cn/machine-learning/crash-course/reducing-loss/learning-rate