为实习准备的数据结构（2）-- 详尽链表篇

华为云博客 技术博客 18321 33

在这里插入图片描述

文章目录

C链表

链表在C语言的数据结构中的地位可不低。后面很多的数据结构，特别是树，都是基于链表发展的。
所以学好链表，后面的结构才有看的必要。

初识链表

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。

但是链表失去了数组随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大。

链表有很多种不同的类型：单向链表，双向链表以及循环链表。

单链表

在这里插入图片描述

单链表实现

话不多说啊，这里我只想直接放代码：

#include <stdio.h>	//初学者，C语言开手
#include <conio.h>
#include <stdlib.h>
#include <memory.h>
#include <assert.h>

//节点数据结构体
typedef struct test
{	
	char name[12];		//名字
	char pwd[8];		//密码
	int number;			//编号
	int flag;			//区分管理员和用户	// 	0 超级管理员 1 管理员  2 普通用户 3 屏蔽用户
	int money;			//仅用户有存款，初始500
} TEST_T;

//如果不多来一个数据域，怎么能体现出通用链表的优势
typedef struct reported
{
	int amount;//交易金额
	int rflag; //交易方式	1、存款 2、取款 3、转账转出 4、转账转入
	int lastmoney;//余额
	int lastmoney2;//收款者的余额
	int number1;//付款账户
	int number2;//入款账户
	char time[12];//操作时间	
} REPORT_T;

//节点描述结构体
typedef struct point
{
	void *pData; //指向数据域
	struct point *next;			//指向下一个节点	
} POINT_T;

POINT_T * head ;
extern POINT_T * head;
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37

这还是个通用链表的头呢！！！

//创建结点
POINT_T * creat(void *data )	//创建一个属于结构体point的函数，
//传入结构体test的指针便可以用以操作test变量，
{ //并返回一个point的指针用以操作point函数
	POINT_T *p=NULL; p=(POINT_T *)malloc(sizeof(POINT_T));
	if(p==NULL)
	{
		printf("申请内存失败");
		exit(-1);
	}
	memset(p,0,sizeof(POINT_T)); p->pData=data;
	p->next=NULL;	//处理干净身后事
	return p;
}

//新增节点
void add(POINT_T * the_head,void *data ) //这里的data不会和上面那个冲突吗？
{
	POINT_T * pNode=the_head; //把头留下
	POINT_T *ls=creat(data);
	//后面再接上一个
	while (pNode->next != NULL) //遍历链表，找到最后一个节点
	{
		pNode=pNode->next;
	}
	pNode->next=ls;			//ls 临时
}

//删除节点
void del(POINT_T * the_head, int index)
{
	POINT_T *pFree=NULL; //用来删除 POINT_T *pNode=the_head;
	int flag=0;
	while (pNode->next!=NULL)
	{
		if(flag==index-1)
		{ pFree=pNode->next; //再指向数据域就爆了 pNode->next=pNode->next->next;	//这里要无缝衔接 free(pFree->pData); //先释放数据 free(pFree); //释放指针 break;
		}
		pNode=pNode->next;
		flag++;	
	}	
}

//计算节点数
int Count(POINT_T * the_head)
{
	int count=0;
	POINT_T *pNode1=the_head;
	while (pNode1->next!=NULL)
	{
		pNode1=pNode1->next;
		count++; }	
	return count;
}

//查找固定节点数据
POINT_T * find(POINT_T *the_head,int index)
{
	int f=0;
	POINT_T *pNode=NULL;
	int count=0;
	pNode=the_head; count=Count(the_head); if(count<index) printf("find nothing"); while(pNode->next!=NULL)
	{
		if(index==f) return pNode;
		pNode=pNode->next;
		f++; }
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88

尾插法

若将链表的左端固定，链表不断向右延伸，这种建立链表的方法称为尾插法。尾插法建立链表时，头指针固定不动，故必须设立一个搜索指针，向链表右边延伸，则整个算法中应设立三个链表指针，即头指针head、搜索指针p2、申请单元指针pl。尾插法最先得到的是头结点。

上面那个就是。

循环链表

在这里插入图片描述

我不喜欢搞的花里胡哨，把循环链表单独拿出来呢，是因为之前有几道题给我留下了印象。

判断链表是否有环

就像那电影里的情节，男主女主在小树林里迷路了，到处都是树，他们兜兜转转，又回到了原点。
链表一旦成环，没有外力的介入是绕不出来的。

我举个栗子：

//ListNode* reverseList(ListNode* head)
//{
// ListNode* node_temp;
// ListNode* new_head;
//
// node_temp = head;
// //遍历一个节点，就把它拿下来放到头去
// while (head->next != NULL)
// {
// //先考虑只又两个节点的情况 
// head = head->next;
// new_head = head;
// new_head->next = node_temp;
// node_temp = new_head;
// }
// return new_head;
//}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17

我也不知道当时是哪儿来的灵感，写出了这么个玩意儿。后来怎么着了？后来卡死了呗，就搁那儿绕圈，绕不出来了。

那要这么去判断一个链表是否有环呢？
其实说简单也简单，快慢指针就解决了，快指针两步走，慢指针一步走，只要两个指针重合了，那就说明有环，因为快指针绕回来了。
时间复杂度为线性，空间复杂度为常数。
说不简单也不简单，因为你去判断一个链表是否有环，那顶多是在测试环节，放在发布环节未免显得太刻意，连代码是否安全都不能保证。

而且，有环的话一般是运行不过的，不用测，运行超时妥妥要考虑一下环的情况，一调试就知道了。

寻找链表入环点

这个就比较需要脑子了，前边那个有手就行的。

我这个人，懒了点，来张现成的图吧。
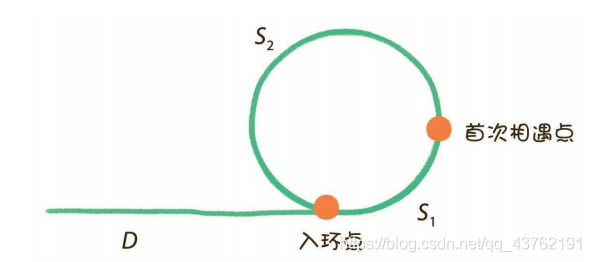
在这里插入图片描述

看啊，在相遇之前呢，慢指针走的距离很好求的：L1 = D+S1;
快指针走的距离：设它在相遇前绕了n圈（n>1），那么：L2 = D+S1+n(S1+S2);

不过，还有一个等量关系，不要忽略掉，快指针的速度是慢指针的两倍，所以：L2 = 2L1;
那么就是：n(S1+S2)-S1 = D;
再转换一下就是：(n-1)(S1+S2)+S2 = D;

那也就是说，在相遇时候，把一个慢指针放在链表头，开始遍历，把一个慢指针放在相遇点开始转圈，当它俩相遇的时候，就是入环点了。

其实吧，用脑子想一开始很难想出来，用手想就快多了。

环的大小就不用我多说了吧，相遇之后，定住快指针，慢指针再绕一圈，再相遇的时候就是一圈了。

双向链表

在这里插入图片描述

参考单链表。

LeetCode 上的链表题

记一段曾经的问题代码

struct ListNode { int val; ListNode* next; ListNode(int x) : val(x), next(NULL) {} };

ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) { //传进来的参数不为空 ListNode* temp1 = list1; ListNode* temp2 = list2; //ListNode* temp3 = new ListNode(0);	这要是放这里了问题就大了 while (temp1->next != NULL && temp2!= NULL) { if (temp1->next->val >= temp2->val) { ListNode* temp3 = new ListNode(0);  //这个要放在这里，新插入的节点一定要是新鲜的 temp3->val = temp2->val;  //这里要注意，对新指针赋值，一定要只赋值给单指针，不要把后面一串全弄过去，会出现环状链表 temp3->next = temp1->next; temp1->next = temp3; temp2 = temp2->next; } temp1 = temp1->next; } if (temp2!= NULL) { temp1->next = temp2; } return list1;
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28

翻转链表

ListNode* reverseList(ListNode* head) 
{ ListNode* node_temp = NULL; //这里设为NULL ListNode* new_head = NULL;   //链栈的头 //遍历一个节点，就把它拿下来放到头去 while (head != NULL) { node_temp = head;   //先将节点取出 //先考虑只又两个节点的情况  head = head->next;  //这个不放这里又成环了 node_temp->next = new_head;
	//刚开始相当于是置空的，因为前面并没有分配空间，而是NULL new_head= node_temp; } return new_head;
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

不好理解啊，这里要明确几点：
1、head是当前遍历的节点，可以看成迭代器。
2、new_head= node_temp，但是node_temp的变化不影响new_head。

旋转链表

这个也比较有意思啊，题目时这样的：给定一个当链表，让你顺时针/逆时针旋转N个位置，要求原地旋转。

我讲一下思路吧：
1、将链表自成环。
2、从刚刚的头往后遍历N个位置，N为要旋转的数。
3、环断开。

解决。
秀吧，我就是觉得解法好玩，就收藏了。

STL 中的 List

每一个自己写过链表的人都知道，链表的节点和链表本身是分开设计的。
那我们来看一下List的节点设计：

template <typename T>
struct __list_node
{
	typedef void* void_pointer;
	void_pointer prev;
	void_pointer neet;
	T date;
}
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

显而易见，这是一个通用双向链表的节点（如果对通用链表不了解，建议一定要自己动手设计一个）。
在这里插入图片描述

3、List基本函数使用

  1. 创
#include<list>

typedef struct rect
{
	···
}Rect;

list<Rect>test;	//声明一个链表，用于存放结构体数据

//如果想以其他方法初始化list列表，可以移步到下一行那个Vector的介绍
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  1. 增
Rect a;
···
test.push_back(a);
test.push_front(a);
//头尾插入（双向链表）

//定点插入
test.insert(test.begin()+10,a);	//在第十个节点之前插入a
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  1. 删
//删除test头部的元素
test.erase(test.begin());

//删除test从头到尾的元素
test.erase(test.begin(), test.end());

test.pop_back();
test.pop_front();
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

其实增删还是推荐使用迭代器来，因为直接对数据进行操作会存在一定的危险。
在本文第三部分详细讲述了List迭代器操作增删。

除了这个函数：test.clear();这个函数安全得很，反正都清理掉了。

  1. 查、改
//迭代器
list<int>::iterator p；
for (p = test.begin(); p != test.end(); p++)
	cout << *p << " ";
  • 1
  • 2
  • 3
  • 4

要遍历还是首推迭代器。所有和遍历有关的还是用迭代器。

  1. 排
#include<algorithm>
sort(test.begin(),test.end());	//从头到尾，默认从小到大排序

//一般排序都是要自定义排序的：
bool Comp(const int &a,const int &b)
{ return a>b;
}
sort(test.begin(),test.end(),Comp);	//这样就降序排序。
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  1. 大小
test.size();	//容器已存入数据量
test.capacity();	//容器还能存多少数据量

//其实不用担心容器不够大，容量要满的时候它会自己扩容
  • 1
  • 2
  • 3
  • 4
  1. 其他
    (1)压缩list
//去除重复的元素至只保留一个副本
test.unique();
//已经过大小排序的list才能使用
  • 1
  • 2
  • 3
	(2)合并list
  • 1
test.splice(test.end(),test2);//将test2剪切到test后面
  • 1

最后还是要提一下头文件：
分不清楚就都写上

#include<algorithm>
#include<list>
  • 1
  • 2

在这里插入图片描述

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/113554786

（完）