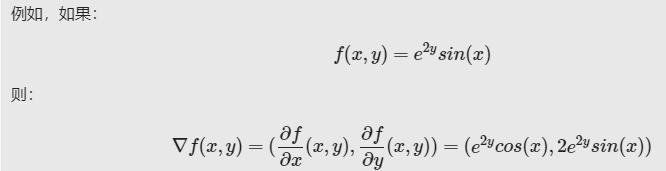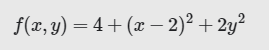机器学习4-模型迭代

2021-06-18 21:25:34 华为云博客技术博客 22597 35

前言

在训练机器学习模型时，首先对权重和偏差进行初始化猜测，然后反复调整这些猜测参数（权重和偏差），直到获得损失可能最低时的，权重和偏差。

训练模型的迭代方法

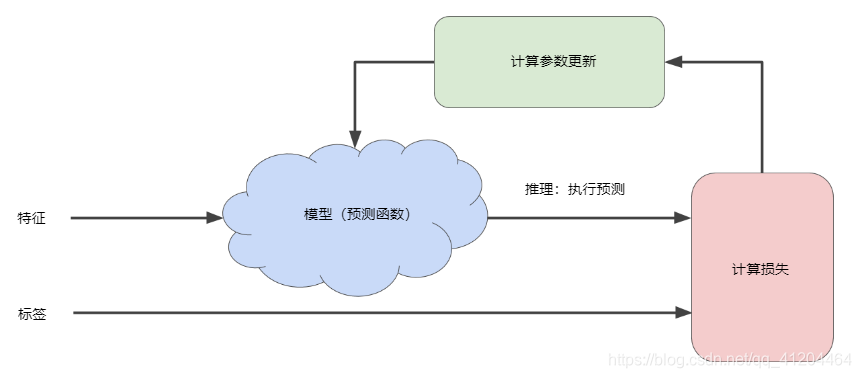
机器学习算法用于训练模型的迭代试错过程：

“模型”部分将一个或多个特征作为输入，然后返回一个预测（ $y^{'}$ ）作为输出。

为了进行简化，不妨考虑采用一个特征，并返回一个预测的模型：

$y^{'} = b + w_{1}x_{1}$

需要考虑为 $b$ 和 $w_{1}$ 设置哪些初始值？对于线性回归问题，事实证明初始值并不重要。（注意：如果是其他模型初始化值可能很重要，具体模型具体处理）。我们可以随机初始化，或者采用以下这些无关紧要的值：

$b$ = 0
$w_{1}$ = 0

假如第一个特征值是10，将该特征值代入预测函数会得到以下结果：

  y' = 0 + 0(10)
  y' = 0

然后需要计算损失，上图中的“计算损失”部分是模型使用损失函数，比如：平方损失函数。

损失函数将采用两个输入值：

$y^{'}$ ：模型对特征x的预测
y：特征x对应的正确标签。

最后，到图中“计算参数更新”部分。机器学习系统就是在此部分检查损失函数的值，并更新 $b$ 和 $w_{1}$ ，即为 $b$ 和 $w_{1}$ 生成新值。

假设这个神秘的绿色框会产生新值，而该值又产生新的参数。这种学习过程会持续迭代，直到该算法发现损失已经降到最低，此时得到一个较好的模型，保存此时的模型参数。

通常，可以不断迭代，直到总体损失不再变化或变化极其缓慢为止，此时模型已经收敛。

关键词（训练、收敛、损失）

训练（training）构建模型的理想参数的过程。

收敛（convergence）收敛通常是指在训练期间达到的一种状态，即经过一定次数的迭代之后，训练损失和验证损失，在每次迭代中的变化都非常小或不再变化。在深度学习中，损失值有时会最终下降之前的多次迭代中保持不变或几乎保持不变，暂时形成收敛的假象。参阅早停法。参阅 Boyd 和 Vandenberghe 合著的 Convex Optimization（《凸优化》）

损失（Loss）一种衡量指标，用于衡量模型的预测偏离其标签程度。要确定此值，模型需要定义损失函数。例如：线性回归模型参与均方误差MAS损失函数，分类模型采用交叉熵损失函数。

梯度下降法

在训练模型的迭代中，“计算参数更新”部分，可以使用梯度下降法实现。

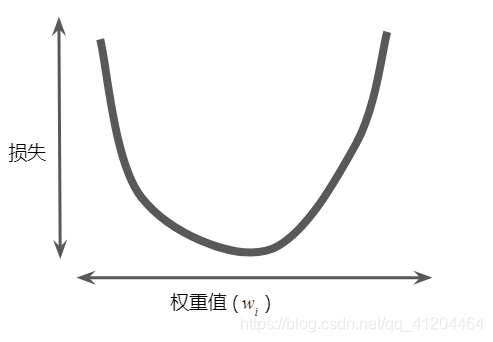
假设我们有时间和计算资源来计算 $w_{1}$ 的所有可能值的损失。对于我们一直在研究的回归问题，所产生的损失与 $w_{1}$ 的图形始终是凸性，如下图所示：

回归问题产生的损失与权重为凸形。

凸形问题只有一个最低点；即只存在一个斜率正好为0的位置。这个最小值就是损失函数收敛之处。

通过计算整个数据集中 $w_{1}$ 每个可能值的损失函数来找到收敛点，这种方法效率太低了。我们来研究一种更好的机制，这种机制在机器学习领域非常热门，称为梯度下降法。

梯度下降法实现流程

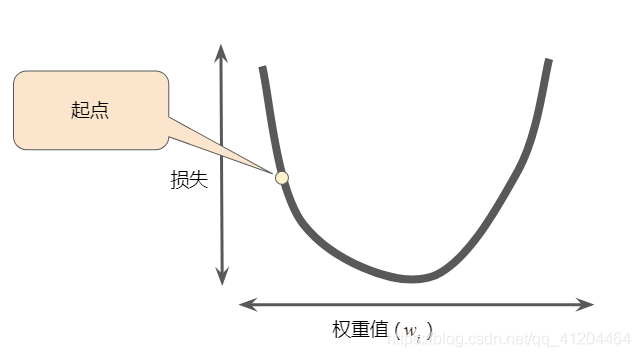
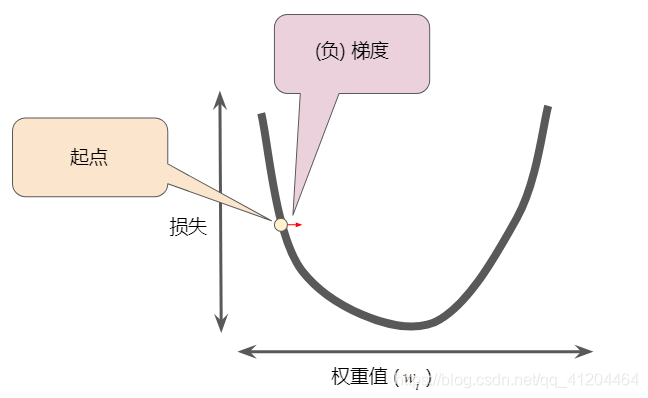
梯度下降法的第一个阶段是为 $w_{1}$ 选择一个初始值（起点），下图显示的是我们选择了一个稍大于0的起点：

然后，梯度下降法会计算损失曲线在起点处的梯度。梯度是偏导数的矢量；它可以让模型了解那个方向距离目标“更近”或“更远”。

详细了解的偏导数和梯度

这里主要用到微积分的知识，通常开源的机器学习框架已经帮我们计算好梯度了，比如像TensorFlow。

偏导数

多变量函数值的是具有多个参数的函数，例如： $f(x,y) = e^{2y} sin(x)$

$f$ 想对于 $x$ 的偏导数表示为： $\frac{\partial f}{\partial x}$ ，也是 $f(x)$ 的导数。

要计算 $\frac{\partial f}{\partial x}$ ，必须使y保持固定不变（因此 $f$ 现在是只有一个变量的函数），然后取 $f$ 相对于 $x$ 的常规导数。例如，当 $y$ 固定为1时，前面的函数变为： $f(x) = e^{2} sin(x)$

这只是一个变量 $x$ 的函数，其导数为： $e^{2} cos(x)$

一般来说，假设 $y$ 保持不变， $f$ 对 $x$ 的偏导数的计算公式如下：

$\frac{\partial f}{\partial x}(x,y) = e^{2y}cos(x)$

同样，如果我们使 $x$ 保持不变， $f$ 对 $y$ 的偏导数为：

$\frac{\partial f}{\partial x}(x,y) = 2e^{2y}sin(x)$

直观而言，偏导数可以让我们了解到，当略微改动一个变量时，函数会发送多大的变化？在前面的示例中：

$\frac{\partial f}{\partial x}(0,1) = e^{2} \approx 7.4$

因此，如果我们将起点设为（0,1），使 $y$ 保持固定不变，并将 $x$ 移动一点， $f$ 的变化量是 $x$ 变化量的7.4倍左右。

在机器学习中，偏导数主要与函数的梯度一起使用。

梯度

函数的梯度是偏导数相当于所有自变量的矢量，表示为：∇ $f$ ，诶，CSDN编辑器打不∇

需要注意的是：

∇ $f$	指向函数增长速度最快的方向。
-∇ $f$	指向函数下降速度最快的方向。

该矢量中的维度个数等于 $f$ 公式中的变量个数；该矢量位于该函数的域空间内。

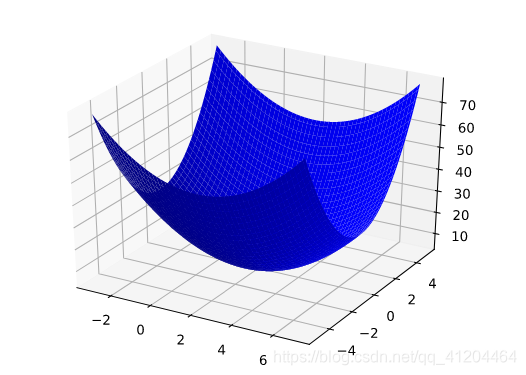
例如，在三维空间中查看下面的函数 $f(x,y)$ 时：

$z = f(x,y)$ 就像一个山谷，最低点为（2,0,4）：

$f(x,y)$ 的梯度是一个二维矢量，可让我们了解向那个方向移动时，高度下降得最快；即：梯度矢量指向谷底。

在机器学习中，梯度用于梯度下降法。我们的损失函数通常具有很多变量，而我们尝试通过跟随函数梯度的负方向来尽量降低损失函数。

需要注意，梯度是一个矢量，因此具有以下两个特征：

方向
大小

梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法会沿着负梯度的方向走一步，以便尽快降低损失。梯度下降法依赖于负梯度：

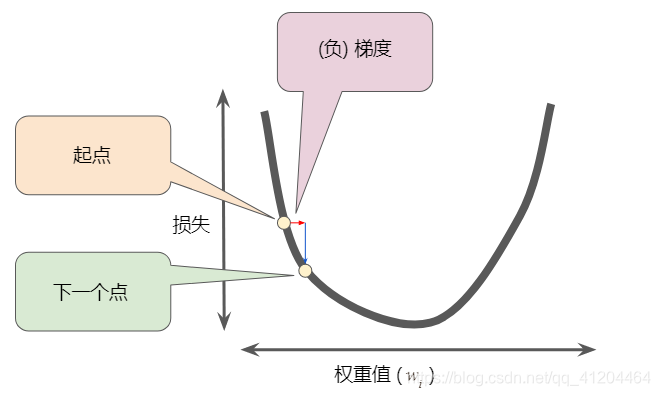
为了确定损失函数曲线上的下一个点，梯度下降法会将梯度大小的一部分与起点相加，如下图所示：

一个梯度步长将我们移动到损失曲线上的下一个点。然后，梯度下降法会重复此过程，逐渐接近最低点。

关键词-梯度下降法

梯度下降法（gradient descent）一种通过计算梯度，并且将损失将至最低的技术，它以训练数据位条件，来计算损失相对于模型参数的梯度。梯度下降法以迭代方式调整参数，逐渐找到权重和偏差的最佳组合，从而将损失降至最低。

参考：https://developers.google.cn/machine-learning/crash-course/reducing-loss/an-iterative-approach

参考：https://developers.google.cn/machine-learning/crash-course/reducing-loss/gradient-descent

（完）