
点击上方bigsai关注我们

前言
一次面试官笑嘻嘻的问我一个问题,场景还原一下:

然后我把这个问题透彻的研究了一下,并由浅入深的分析了一下这种问题的思路,分别是有几个pat和不同子序列问题。
有几个pat
这是pat的一道题。

分析
如何求一个字符串中有多少个pat。不要想着三重for循环去枚举所有情况了,那不是好的方法。这这种题如果有灵感的话应该能猜出来这应该是一种动态规划的问题。
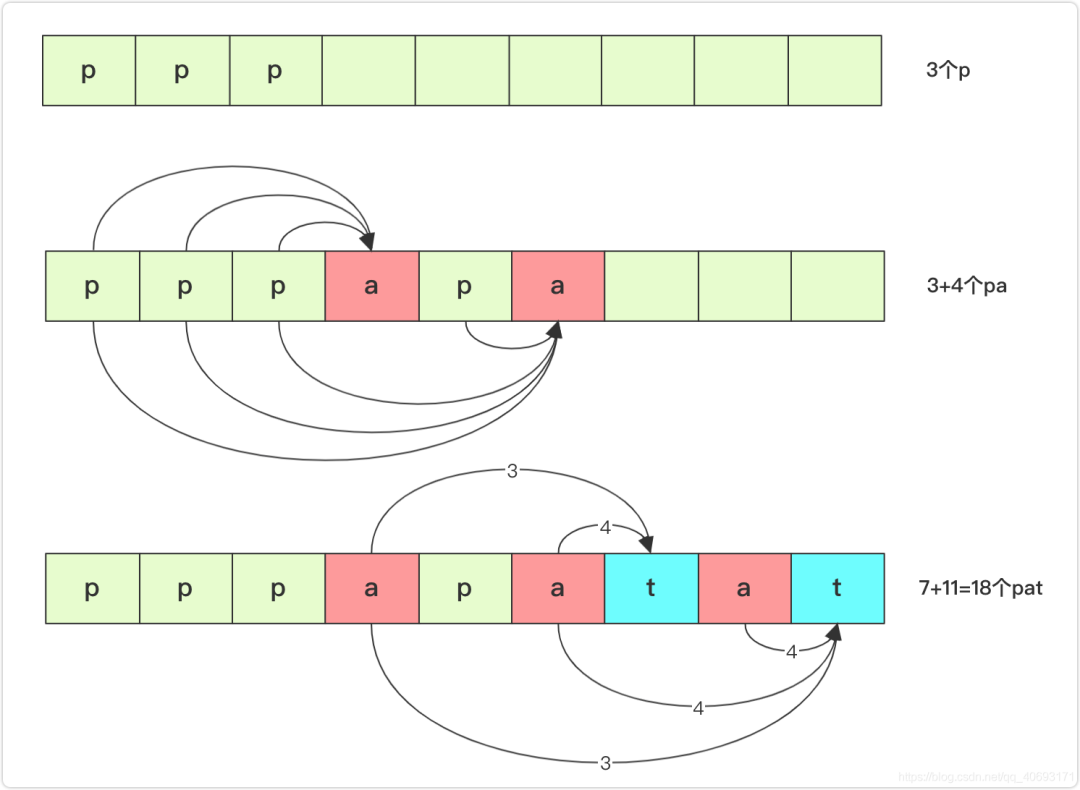
首先将问题简单分解一下,如果问原串中有多少个p。那么很容易枚举一遍即可。例如序列ppp就是三个p。
如果带上a,求串pa的个数呢?pa是由p和a组成。求pa的个数肯定和a有很大的关系,每个a可能会组成若干个pa取决于这个a前面p的数量。将所有a位置组成的pa相加即可。例如pppapa 总共可以组合3+4=7个pa.
同理想知道有几个pat那也很容易啊,pat的求解需要找到每个t,然后知道当前位置前面有多少个pa,叠加求解获得结果即可。结合下图流程看更好。
不同的子序列
题目描述:
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
题目数据保证答案符合 32 位带符号整数范围。
示例 1:
-
输入:s = "rabbbit", t = "rabbit"
-
输出:3
-
解释:
-
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
-
(上箭头符号 ^ 表示选取的字母)
-
rabbbit
-
^^^^ ^^
-
rabbbit
-
^^ ^^^^
-
rabbbit
-
^^^ ^^^
示例 2:
-
输入:s = "babgbag", t = "bag"
-
输出:5
-
解释:
-
如下图所示, 有 5 种可以从 s 中得到 "bag" 的方案。
-
(上箭头符号 ^ 表示选取的字母)
-
babgbag
-
^^ ^
-
babgbag
-
^^ ^
-
babgbag
-
^ ^^
-
babgbag
-
^ ^^
-
babgbag
-
^^^
提示:
0 <= s.length, t.length <= 1000
s 和 t 由英文字母组成
分析:
这个问题其实就是上面有几个pat的变形拓展,其基本思想其实是一致的,上面那题问的是有几个pat,固定、且很短。但这里面t串的长度不固定,所以处理上就要使用数组来处理而不能直接if else。
这题的思路肯定也是动态规划dp了,dp[j]的意思就是t串中[0,j-1]长字符在s中能够匹配的数量(当然这个值从前往后是动态变化的),数组大小为dp[t.length+1]。在遍历s串的每一个元素都要和t串中所有元素进行对比看看是否相等,如果s串枚举到的这个串和t串中的第j个相等。那么dp[j+1]+=dp[j]。你可能会问为啥是dp[j+1],因为第一个元素匹配到需要将数量+1,而这里为了避免(判断是否为首字符)这样的判断我们将dp[0]=1,这样t串的每个元素都能正常的操作。
但是有一点需要注意的就是在遍历s串中第i个字母的时候,遍历t串比较不能从左向右而必须从右向左。因为在遍历s串的第i个字符在枚举dp数组时候要求此刻数据是相对静止的叠加(即同一层次不能产生影响),而从左往右进行遇到相同字符会对后面的值产生影响。区别的话可以参考下图这个例子:

实现的代码为:
-
class Solution {
-
public int numDistinct(String s, String t) {
-
char s1[]=s.toCharArray();
-
char t1[]=t.toCharArray();
-
-
int dp[]=new int[t1.length+1];
-
dp[0]=1;//用来叠加
-
-
for(int i=0;i<s1.length;i++)
-
{
-
for(int j=t1.length-1;j>=0;j--)
-
{
-
if(t1[j]==s1[i])
-
{
-
dp[j+1]+=dp[j];
-
}
-
}
-
}
-
return dp[t1.length];
-
}
-
}
原创不易,如果觉得有所收获,希望大家点赞、分享、在看一键三连帮忙扩散,谢谢!
推荐阅读:
我和蓝桥杯的那两年咱们下次再见!关注后欢迎加我加入力扣打卡群。
点个在看你最好看
文章来源: bigsai.blog.csdn.net,作者:Big sai,版权归原作者所有,如需转载,请联系作者。
原文链接:bigsai.blog.csdn.net/article/details/115019101