BFS算法框架
BFS算法和DFS算法属于图论算法的范畴,DFS在前面回溯中,可以去看一下。
BFS算法用于寻找两点之间的最短路径。
碧如说:寻找树的最小高度(迭代法)、走迷宫、导航等问题。
这些问题看起来都会比较抽象,去做也是很抽象。
与其说算法框架难写,倒不如说是把实际问题转化为算法问题来的要难。
还记得我在图论算法那篇里面有讲过:学习图论算法,最难的是要有用图论算法的意识。等下看了例题就知道了。
框架代码
这个代码其实就是微调一下图的BFS遍历,搞成个伪代码的样子,没什么新鲜的。
int BFS(Node start,Node target){
/*
这是一个BFS算法的代码框架
return:返回从start到target的最短步数
start:起始点
target:终点
*/ Queue<Node> q;
Set<Node> visited; //避免走回头路 q.offer(start); //将起点加入队列
visited.add(start);
int step = 0; //纪录扩散的步数
while(q not empty){
int sz = q.size();
for(int i = 0; i<sz; i++){ Node cur = q.poll(); //判断是否到终点 if(cur is target) return step; //将cur相邻节点加入队列 for(Node x: cur.adj()) //cur.adj()泛指与cur相邻的节点 if(x not in visited){ q.offer(x); visited.add(x); }
} step++; //更新步数
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
简单题:二叉树的最小高度
不难吧,用递归的话一下就出来了。
不过现在不是在讲BFS嘛,那就用BFS的方法吧。
起点是什么?起点是根节点。终点是什么?终点就是最靠近根节点的、两个子节点都是Null的节点。
接下来,我们对上面的框架进行改造:
int minDepth(TreeNode root){
/*
这是一个求二叉树最小高度的函数
return:二叉树的最小高度
root:根节点
*/
if(root == NULL) return 0; Queue<TreeNode> q;
q.offer(root); //将起点加入队列
int depth = 1; while(!q.isEmpty()){
int sz = q.size();
for(int i = 0; i<sz; i++){ TreeNode cur = q.poll(); //判断是否到终点 if(cur.left == NULL && cur.right == NULL) return depth; //将cur相邻节点加入队列 if(cur.left != NULL) q.offer(cur.left); if(cur.right != NULL) q.offer(cur.right);
} depth++; //更新步数
}
return depth;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
拔高题:解开密码锁的最少次数
你有一个带有四个圆盘拨轮的轮盘锁,每个拨轮都有“0-9”十个数字,旋转没有边界限制,但是每次只能旋转一个位置。轮盘锁的初始位置是“0000”,现在给你一个密码和一组死亡密码(避免拨出的密码),请你设计一个算法,计算从初始状态到拨出最终密码所需要的最少次数。
抽象吧,就直接看这个题目,直接给我干懵逼了。
但是,不怕啊,前面不是说过了动态规划类题目的解题步骤嘛,先把暴力解法画出来,走通一条路,再优化。
那,暴力解法怎么解?真的,要不是有那个“死亡密码组”的存在,还真的就很暴力了。
第一步,拨一下。不管会怎么样,都得拨一下吧。这一下有八种可能了吧。
第二步,匹配。拨一下,对所有结果都进行一次的匹配。如果对上了,就返回结果;如果对不上,返回第一步再循环。
注意点一:如果碰到死亡密码,跳过。
注意点二:不要走回头路。
注意点三:空间能省着用就省着用。
- 1
- 2
- 3
- 4
- 5
好,关键的一步来了,怎么将这个暴力算法往图论算法的方向去引呢。
再看一下上面这个暴力算法,不难看出来,这就是一个节点下面拖八个子节点的八叉树,又是求最短距离,BFS。
int openLock(String[] deadends,String target){
//纪录需要跳过的死亡密码
Set<String> deads = new HashSet<>(); for(String s:deadends) dead.add(s);
//纪录已经穷举过的密码
set<String> visited = new HashSet<>(); Queue<String> q = new LinkedList<>(); //从起点开始启动广度优先搜索
int step = 0;
q.offer("0000");
visited.add("0000");
while(!q.isEmpty){
int sz = q.size();
for(int i = 0;i<sz;i++){ string cur = q.poll(); //判断密码是否合法 if(deads.contains(cur) continue; if(cur.equals(target)) return step;
} //将一个节点的未遍历相邻节点加入队列
for(int j=0;j<4;j++){ String up = plusOne(cur,j); if(!visited.contains(up){ q.offer(up); visited.add(up); } String down = minusOne(cur,j); if(!visited.contains(down){ q.offer(down); visited.add(down); }
}
step++;
}
return -1;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
上翻下翻的代码:
String plusOne(String s,int j){
char[] ch = s.toCharArray();
if(ch[j] == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
String downOne(String s,int j){
char[] ch = s.toCharArray();
if(ch[j] == '0')
ch[j] = '9';
else
ch[j] -= 1;
return new String(ch);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
一波优化:双向BFS
上面的操作,简化一下是这样的:
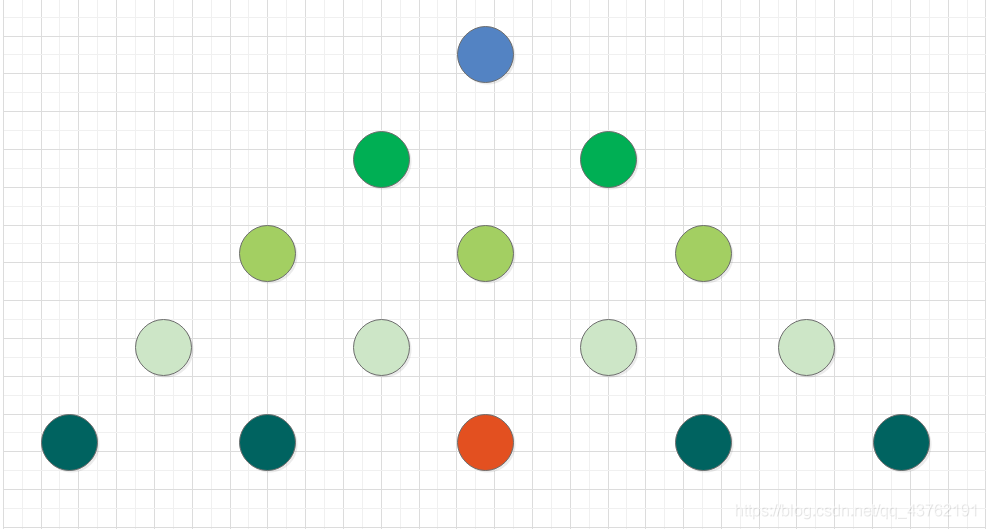
从顶部蓝色的节点,找底部红色的节点。
所有节点都被遍历了。
这时候我们换个思路,既然终点也是已知的,那就:
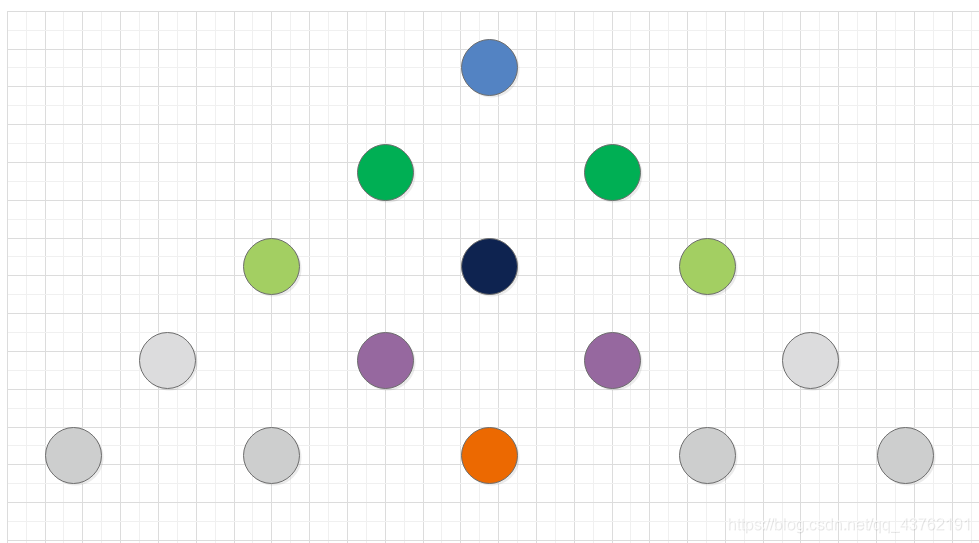
上下同步进行,在中间黑色节点的地方汇聚了。
文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/113915792
