【C++】算法集锦（6）：快慢指针

在这里插入图片描述

文章目录

双指针解法

这是我很喜欢的一个解法，从我第一眼看到它就很喜欢了。

什么时候会用到双指针呢？但凡可以出现两条或者更多序列的时候，就可以用这种方法了。
注意，我说的是：可以出现。有条件要上，没有条件创造条件也要上。

直接上例子吧，这算法太常见了。

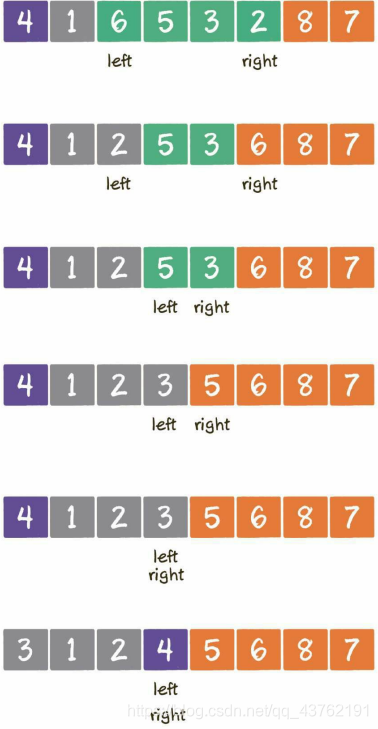
快排

双边遍历

在这里插入图片描述

首先啊，确定基准为4，左指针指向第一个元素，右指针指向尾巴。

在这里插入图片描述

左指针开始，向前遍历，找到第一个大于基准的元素就停下，轮到右指针，同理。

当两个指针都停下之后，将两个指针所指向的值互换位置。

在这里插入图片描述

重复上述步骤直到左右指针重合。

重合之后，将基准元素与左右指针当前位置元素进行互换。

一次循环之后，重复上述动作，对划分出的部分再次循环，直到每个部分都只有一个元素为止。

#include<iostream>
#include<vector>

using namespace std;

void doubleSideSort(vector<int> &vec1,int left,int right)	//序列与左右指针传入
{
	//结束语
	if (right == left)
		return;

	//基准确定
	int flag = vec1[left];

	int keep_right = right;
	int keep_left = left;
	int change_temp;

	//当左右指针还没重合
	while (left<right)
	{
		//左指针先走
		while (left<right && vec1[left]<=flag)
		{ left++;
		}//当遇到比基准大的数，停下来 //轮到右指针走
		while (left < right && vec1[right] >= flag)	//可以都等，反正最后都会归并
		{ right--;
		}//当遇到比基准小的数，停下来 if (left < right)
		{ change_temp = vec1[left]; vec1[left] = vec1[right]; vec1[right] = change_temp;
		} //然后继续循环
	}

	//left--;

	//接着将基准放进去，此时必定是左右相合，则左值若大于左值左边一位，和左值左边一位换，若小，则和左值换
	if (vec1[left] > vec1[left - 1])
	{
		vec1[keep_left] = vec1[left-1];
		vec1[left-1] = flag;
	}
	else
	{
		vec1[keep_left] = vec1[left];
		vec1[left] = flag;
	}

	doubleSideSort(vec1,0,left-1);
	doubleSideSort(vec1, right, keep_right);
}

int main()
{
	vector<int> vec1 = { 4,6,8,7,9,3,1};	//测试用2个数测试最直观，因为最后都要通过这一步才能正常
	int left = 0;
	int right = vec1.size() - 1;

	doubleSideSort(vec1, left, right);

	for (; left <= right; left++)
		cout << vec1[left] << " ";
	cout << endl;

	return 0;
	
}

链表成环

判断链表是否有环

就像那电影里的情节，男主女主在小树林里迷路了，到处都是树，他们兜兜转转，又回到了原点。
链表一旦成环，没有外力的介入是绕不出来的。

我举个栗子：

//ListNode* reverseList(ListNode* head)
//{
// ListNode* node_temp;
// ListNode* new_head;
//
// node_temp = head;
// //遍历一个节点，就把它拿下来放到头去
// while (head->next != NULL)
// {
// //先考虑只又两个节点的情况 
// head = head->next;
// new_head = head;
// new_head->next = node_temp;
// node_temp = new_head;
// }
// return new_head;
//}

我也不知道当时是哪儿来的灵感，写出了这么个玩意儿。后来怎么着了？后来卡死了呗，就搁那儿绕圈，绕不出来了。

那要这么去判断一个链表是否有环呢？
其实说简单也简单，快慢指针就解决了，快指针两步走，慢指针一步走，只要两个指针重合了，那就说明有环，因为快指针绕回来了。
时间复杂度为线性，空间复杂度为常数。
说不简单也不简单，因为你去判断一个链表是否有环，那顶多是在测试环节，放在发布环节未免显得太刻意，连代码是否安全都不能保证。

而且，有环的话一般是运行不过的，不用测，运行超时妥妥要考虑一下环的情况，一调试就知道了。

寻找链表入环点

这个就比较需要脑子了，前边那个有手就行的。

我这个人，懒了点，来张现成的图吧。
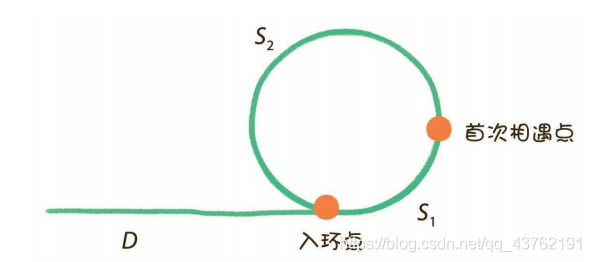
在这里插入图片描述

看啊，在相遇之前呢，慢指针走的距离很好求的：L1 = D+S1;
快指针走的距离：设它在相遇前绕了n圈（n>1），那么：L2 = D+S1+n(S1+S2);

不过，还有一个等量关系，不要忽略掉，快指针的速度是慢指针的两倍，所以：L2 = 2L1;
那么就是：n(S1+S2)-S1 = D;
再转换一下就是：(n-1)(S1+S2)+S2 = D;

那也就是说，在相遇时候，把一个慢指针放在链表头，开始遍历，把一个慢指针放在相遇点开始转圈，当它俩相遇的时候，就是入环点了。

其实吧，用脑子想一开始很难想出来，用手想就快多了。

环的大小就不用我多说了吧，相遇之后，定住快指针，慢指针再绕一圈，再相遇的时候就是一圈了。

合并K个有序链表（困难）

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:

[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6

思路：

将 k 个链表配对并将同一对中的链表合并；
第一轮合并以后， k 个链表被合并成了 k\2个链表，平均长度为 2n\k，然后是 k\4个链表， k\8 个链表等等；
重复这一过程，直到我们得到了最终的有序链表。

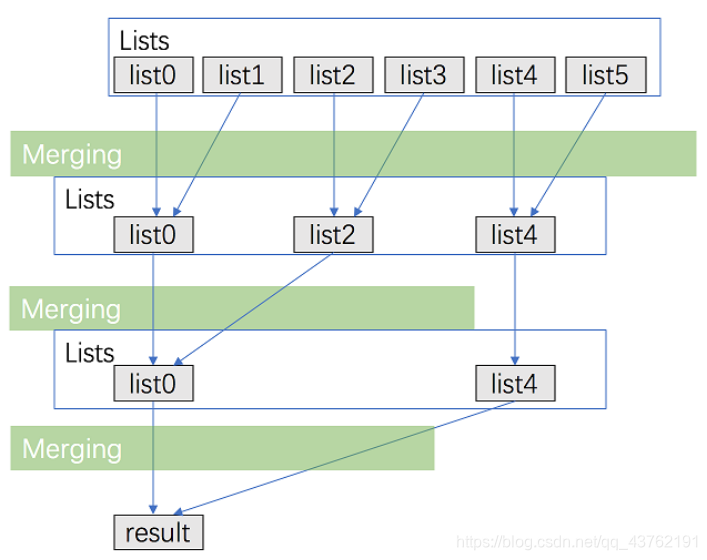
在这里插入图片描述

代码实现：

class Solution {
public: ListNode* mergeTwoLists(ListNode *a, ListNode *b) { if ((!a) || (!b)) return a ? a : b; ListNode head, *tail = &head, *aPtr = a, *bPtr = b; while (aPtr && bPtr) { if (aPtr->val < bPtr->val) { tail->next = aPtr; aPtr = aPtr->next; } else { tail->next = bPtr; bPtr = bPtr->next; } tail = tail->next; } tail->next = (aPtr ? aPtr : bPtr); return head.next; } ListNode* merge(vector <ListNode*> &lists, int l, int r) { if (l == r) return lists[l]; if (l > r) return nullptr; int mid = (l + r) >> 1; return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r)); } ListNode* mergeKLists(vector<ListNode*>& lists) { return merge(lists, 0, lists.size() - 1); }
};

在这里插入图片描述

寻找链表中的倒数第K个元素

思路也挺直接的，先让一个指针走K步，然后从头再放一个指针，两个指针同时走，当前面的指针走到头的时候，后面那个指针所在的位置就是倒数第K个元素了。

代码我就不写了吧。

只要序列有序，我们就应该想到快慢指针。
快慢指针有一个高级进化：滑动窗口，看看要不明天给安排上吧。

在这里插入图片描述

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/113946230

（完）