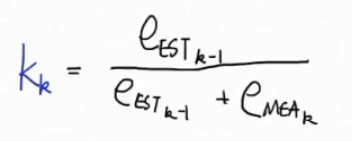卡尔曼滤波器1——递归算法（笔记篇 + 代码实现）

前言

本文是观看DR_CAN老师的视频后，简单总结了一下的笔记，并根据思路写了示例代码；这里主要讲卡尔曼滤波器与递归算法。

视频地址：https://www.bilibili.com/video/BV1ez4y1X7eR

一、卡尔曼滤波器

卡尔曼滤波器，Kalmen Filter；可理解为是一种算法：最优化递归数字处理算法。它更像一种观测器，而不是一般意义的滤波器。卡尔曼滤波器应用非常广泛，主要是因为很多事物存在不确定性，不确定性体现在三个方面：

不存在完美的数学模型；
系统存在扰动，或很难建模；
测量传感器存在误差。

二、引言案例测量硬币尺寸

不同的人员，测量同一个硬币，测量结果用 $Z_{k}$ 表示，其中k是表示第k次测量；这里产生误差或不确定地方有：尺子本身的误差、不同人员测试的。

第一次测量结果， $Z_{1}$ = 50.1mm；

第二次测量结果， $Z_{2}$ = 50.4mm；

第三次测量结果， $Z_{3}$ = 50.2mm；

如果让我们“估计真实数据”，自然会想到取三次结果的平均值。估计值 $\hat{x_{k}}$ ，用平均值表示：

$\hat{x_{k}} =\frac{1}{k}(Z_{1}+Z_{2}+........+Z_{k})$

$= \frac{1}{k}(Z_{1}+Z_{2}+........+Z_{k-1}) + \frac{1}{k}Z_{k}$

$= \frac{1}{k}\frac{k-1}{{\color{Red} k-1}}{\color{Red} (Z_{1}+Z_{2}+........+Z_{k-1})} + \frac{1}{k}Z_{k}$ 注释：红色部分是k-1次的平均值， $\hat{x_{k-1}}$

$= \frac{k-1}{k} \hat{x_{k-1}}+ \frac{1}{k}Z_{k}$

$= \hat{x_{k-1}} -\frac{1}{k}\hat{x_{k-1}}+\frac{1}{k}Z_{k}$

重新整理后得到： $\hat{x_{k}} = \hat{x_{k-1}}+\frac{1}{k}(Z_{k}- \hat{x_{k-1}})$ ，其代表的含义是：

本次的估计值 = 上一次的估计值 + 系数*(本次测量值 - 上一次的估计值)

观察一下k变化的影响，k是测量的次数：

当k很大时， $\frac{1}{k}$ 趋于0，这时估计值 $\hat{x_{k}} = \hat{x_{k-1}}$ ，即：测试的次数很多后，本次的估计值，和上一次的估计值很接近了。

当k很小时， $\frac{1}{k}$ 趋于1，这时估计值 $\hat{x_{k}}=Z_{k}$ ，即：测试的次数很少后，本次的估计值，取本次测量值更准确一些。

三、卡尔曼公式

综上所得，卡尔曼公式如下，含义也简单解释一下：

本次的估计值 = 上一次的估计值 + 系数*(本次测量值 - 上一次的估计值)

$\hat{x_{k}}= \hat{x_{k-1}} + K_{k}(Z_{k} - \hat{x_{k-1}})$

其中 $K_{k}$ ，Kalman Gain，表示卡尔曼增益/因素

通过公式可以看出来，本次的估计值 $\hat{x_{k}}$ ，与上一次的估计值 $\hat{x_{k-1}}$ 有关。然后上一次的估计值，由与上上次的估计值有关；这是一种递归的思想。

这也是卡尔曼滤波器的优势，它不需要追溯很久以上的数据，只需拿上一次的数据就可以了。

四、卡尔曼增益 Kalman Gain

如何计算这个卡尔曼增益，这里给出一个公式，后面有机会再详细解释和推导。在此之前，首先介绍两个概念：

估计误差 $e_{EST}$ ，其中e是指error，误差的意思。EST是指Estimate，估计的意思。

测量误差 $e_{MEA}$ ，MEA是指Measure，测量的意思。真实值和测量值之间的误差。

卡尔曼增益 $K_{k}$ 公式如下：（小k是指计算次数；k-1是k的上一次。）

卡尔曼增益 = 上一次的估计误差 除以 (上一次的估计误差 + 本次的测量误差)

五、更新估计误差 $e_{EST}$

估计误差在每次计算中，需要更新的，具体的公式如下：

公式含义：本次的估计误差 = （1 - 卡尔曼增益）* 上一次的估计误差

六、卡尔曼计算流程

首先计算卡尔曼增益 $K_{k}$ ，然后计算本次的估计值 $\hat{x_{k}}$ ，最后更新估计误差 $e_{EST}$ 。

第一步：卡尔曼增益 = 上一次的估计误差除以 (上一次的估计误差 + 本次的测量误差)

第二步：本次的估计值 = 上一次的估计值 + 系数*(本次测量值 - 上一次的估计值)

第三步：本次的估计误差 = （1 - 卡尔曼增益）* 上一次的估计误差

如果错误请指出，谢谢；欢迎多多交流。

七、实例应用卡尔曼算法

前面讲了这么多理论的，可能不是太清晰，下面用测量硬币的例子，观察一下卡尔曼滤波的魅力。

硬币实际长度：50mm

用尺子手动测量误差是：3mm （即：测出来的结果范围在47mm——53mm之间）

假设模型M能估计硬币的长度

首先让模型M估计一个结果，比如：认为硬币只有40mm；估计误差可能是5mm。

按照卡尔曼算法流程，首先计算卡尔曼增益 $K_{k}$ ，然后计算本次的估计值 $\hat{x_{k}}$ ，最后更新估计误差 $e_{EST}$ 。即：

画一个表格，观察预测值，和手动测量值变化：

k	$Z_{k}$ 测量值	$e_{MEA.k}$ 测量误差	$k_{k}$ 卡尔曼增益	$\hat{x_{k}}$ 估计值	$e_{EST.k}$ 估计误差
0				40	5
1	52	3	0.625	47.7	1.875
2	51	3	0.385	48.847	1.153
3	47	3	0.278	48.334	0.832
4	52	3	0.217	49.13	0.651
5	49	3	0.178	49.10	0.535

能看虽然手动测量不稳定，存在3mm的误差，但经过卡尔曼滤波后，输出的估计逐渐趋于真实值50，而且也比较稳定。

k =1；第一次手动测量为52mm

$k_{1} = \frac{5}{5+3}=0.625$

$\hat{x_{1}} = 40 + 0.625 (52 - 40)=47.5$

$e_{EST.1} = (1-0.625)*5=1.875$

k =2；第二次手动测量为51mm

$k_{2} = \frac{1.875}{1.857+3}=0.385$

$\hat{x_{2}} = 47.5 + 0.385 (51 - 47.5)=48.847$

$e_{EST.2} = (1-0.385)*1.875=1.153$

后面的可以自己推算一下。

八、卡尔曼滤波-递归算法 Python版

根据卡尔曼滤波的流程，用Python写了一个代码，对应上面测量硬币的案例：

'''
卡尔曼滤波器--递归算法
Author: guopu
date: 2021-8-23
'''


k = 0        # 计算次数

msa = 0      # 手动测量结果
e_MEA = 0.0  # 手动测量误差

X_k0 = 0.0   # 上一次估计结果
X_k = 0.0    # 本次估计结果

e_EST0 = 0.0 # 上一次估计误差
e_EST = 0.0  # 本次估计误差

KK = 0.0     # 卡尔曼增益

'''
卡尔曼增益 = 上一次的估计误差 除以 (上一次的估计误差 + 本次的测量误差)
'''
def kalman_gain(e_EST0, e_MEA):
    return e_EST0/(e_EST0 + e_MEA)

'''
本次的估计值 = 上一次的估计值 + 系数*(本次测量值 - 上一次的估计值)
'''
def now_estimated_value(X_k0, kk, msa):
    return X_k0 + kk*(msa - X_k0)

'''
本次的估计误差 = （1 - 卡尔曼增益）* 上一次的估计误差
'''
def now_estimated_error(KK, e_EST0):
    return (1 - KK)*e_EST0


# 初始化数据 
true_Length = 50.0                # 硬币的真实长度
msa_list = [52, 51, 47, 52, 49]   # 5次的手动测量结果
e_MEA = 3.0                       # 手动测量误差
X_k = 40.0                        # 初始估计结果
e_EST = 5.0                       # 初始估计误差

X_list = []                      # 用来存放估计值


for k in range(0, len(msa_list)):
    KK = kalman_gain(e_EST, e_MEA)
    X_k = now_estimated_value(X_k, KK, msa_list[k])
    e_EST = now_estimated_error(KK, e_EST)

    print("\n k:", k+1)
    print("测量结果:", msa_list[k])
    print("估计结果:", X_k)
    X_list.append(X_k)

print("\n真实长度", true_Length)
print("\n5次测量结果:", msa_list)
print("\n5次估计结果:", X_list)
print("\n")

代码效果：

本文只提供参考和学习，谢谢。

（完）

前言