一、题目内容

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的体力值是路径上相邻格子之间高度差绝对值的最大值决定的。

请你返回从左上角走到右下角的最小体力消耗值。

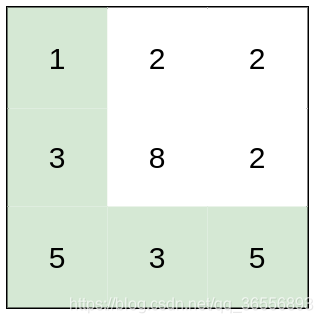
示例 1：

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

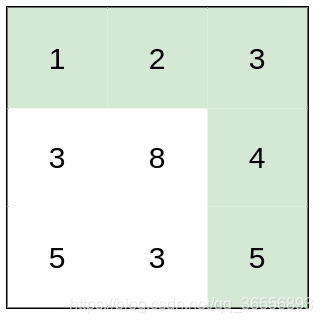
示例 2：

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

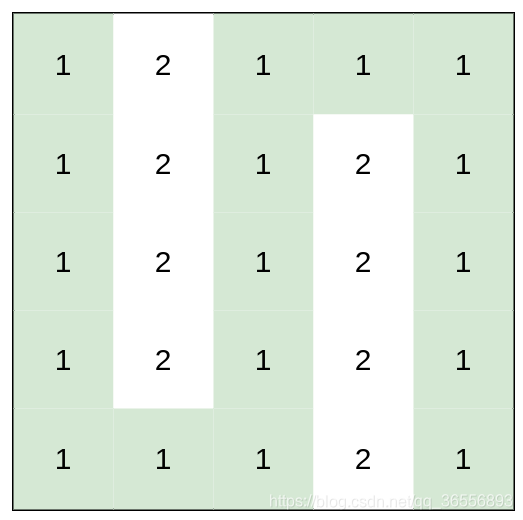
示例 3：

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10^6

二、解题思路

并查集，存储x到y的距离，然后按照距离从小到大排序，之后从小到大遍历每个距离，每次存储当前距离和记录的距离最大值中二者大的一方，最后返回最大的距离。

三、代码


  
   
    
     
    
    
     
      class Solution:
     
    
   
    
     
    
    
      def minimumEffortPath(self, heights: list) -> int:
     
    
   
    
     
    
    
     
       f = list(range(len(heights) * len(heights[0])))
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
      def find(x):
     
    
   
    
     
    
    
      if x != f[x]:
     
    
   
    
     
    
    
     
       f[x] = find(f[x])
     
    
   
    
     
    
    
      return f[x]
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
      def union(x, y):
     
    
   
    
     
    
    
     
       fx = find(x)
     
    
   
    
     
    
    
     
       fy = find(y)
     
    
   
    
     
    
    
     
       f[fx] = fy
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
      # 存储x到y的边[x, y, distance]
     
    
   
    
     
    
    
     
       x_to_y_list = []
     
    
   
    
     
    
    
      for x in range(len(heights)):
     
    
   
    
     
    
    
      for y in range(len(heights[0])):
     
    
   
    
     
    
    
     
       next_x = x + 1
     
    
   
    
     
    
    
     
       next_y = y
     
    
   
    
     
    
    
      if 0 <= next_x < len(heights) and 0 <= next_y < len(heights[0]):
     
    
   
    
     
    
    
     
       distance = abs(heights[x][y] - heights[next_x][next_y])
     
    
   
    
     
    
    
     
       x_to_y_list.append([x * len(heights[0]) + y,
     
    
   
    
     
    
    
     
       next_x * len(heights[0]) + next_y,
     
    
   
    
     
    
    
     
       distance])
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
     
       next_x = x
     
    
   
    
     
    
    
     
       next_y = y + 1
     
    
   
    
     
    
    
      if 0 <= next_x < len(heights) and 0 <= next_y < len(heights[0]):
     
    
   
    
     
    
    
     
       distance = abs(heights[x][y] - heights[next_x][next_y])
     
    
   
    
     
    
    
     
       x_to_y_list.append([x * len(heights[0]) + y,
     
    
   
    
     
    
    
     
       next_x * len(heights[0]) + next_y,
     
    
   
    
     
    
    
     
       distance])
     
    
   
    
     
    
    
      # 将x到y的边按照distance从小到大排序
     
    
   
    
     
    
    
     
       sorted_x_to_y_list = sorted(x_to_y_list, key=lambda x: x[-1])
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
     
       res = 0
     
    
   
    
     
    
    
      for x_to_y_and_distance in sorted_x_to_y_list:
     
    
   
    
     
    
    
      # 左上与右下连通，直接返回
     
    
   
    
     
    
    
      if find(0) == find(len(heights) * len(heights[0]) - 1):
     
    
   
    
     
    
    
      return res
     
    
   
    
     
    
    
      else:
     
    
   
    
     
    
    
     
       x, y, distance = x_to_y_and_distance
     
    
   
    
     
    
    
      # x和y不连通， 则连通x和y
     
    
   
    
     
    
    
      if find(x) != find(y):
     
    
   
    
     
    
    
     
       union(x, y)
     
    
   
    
     
    
    
      # 判断当前距离和最大值，取大者
     
    
   
    
     
    
    
     
       res = max(res, distance)
     
    
   
    
     
    
    
      return res
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
      
     
    
   
    
     
    
    
     
      if __name__ == '__main__':
     
    
   
    
     
    
    
     
       s = Solution()
     
    
   
    
     
    
    
     
       heights = [[1, 2, 2],
     
    
   
    
     
    
    
     
       [3, 8, 2],
     
    
   
    
     
    
    
     
       [5, 3, 5]]
     
    
   
    
     
    
    
     
       ans = s.minimumEffortPath(heights)
     
    
   
    
     
    
    
     
       print(ans)

文章来源: nickhuang1996.blog.csdn.net，作者：悲恋花丶无心之人，版权归原作者所有，如需转载，请联系作者。

原文链接：nickhuang1996.blog.csdn.net/article/details/113373849

（完）