一说到字符串匹配算法,不知道会有多少小伙伴不由自主的想起那个kmp算法呢?
想到是很正常的,谁让它那么优秀呢。
BF算法
不要被事物的表面现象所迷惑,这个算法全称:Brute Force,有个拉风的中文名:暴力匹配算法。
能想明白了吧。
如果模式串长度为 m,主串长度为 n,那在主串中,就会有 n-m+1 个长度为 m 的子串,我们只需要暴力地对比这 n-m+1 个子串与模式串,就可以找出主串与模式串匹配的子串。
1、从头开始往后遍历匹配;
2、遇上不对了,就回头,把子串和主串的匹配头后移一位
3、重复以上。直到找到或确定找不到。
- 1
- 2
- 3
复杂度很高啊,但是在实际开发中也是比较常用的。为什么呢?
真当天天都有成千上万个字符的主串让我们去匹配吗?一般都比较短,而且,统计意义上,算法执行效率不会真的到M*N的地步。
理论还是要结合实际的。
还有另一个原因,就是它好写。当然kmp现在更好写,因为封装好了。
我说的是类似的场景,没有封装好的函数时候,好写,好改。
RK算法
RK 算法的思路是这样的:我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了(这里先不考虑哈希冲突的问题,后面我们会讲到)。因为哈希值是一个数字,数字之间比较是否相等是非常快速的,所以模式串和子串比较的效率就提高了。
有没有方法可以提高哈希算法计算子串哈希值的效率呢?
我们假设要匹配的字符串的字符集中只包含 K 个字符,我们可以用一个 K 进制数来表示一个子串,这个 K 进制数转化成十进制数,作为子串的哈希值。
比如要处理的字符串只包含 a~z 这 26 个小写字母,那我们就用二十六进制来表示一个字符串。我们把 a~z 这 26 个字符映射到 0~25 这 26 个数字,a 就表示 0,b 就表示 1,以此类推,z 表示 25。
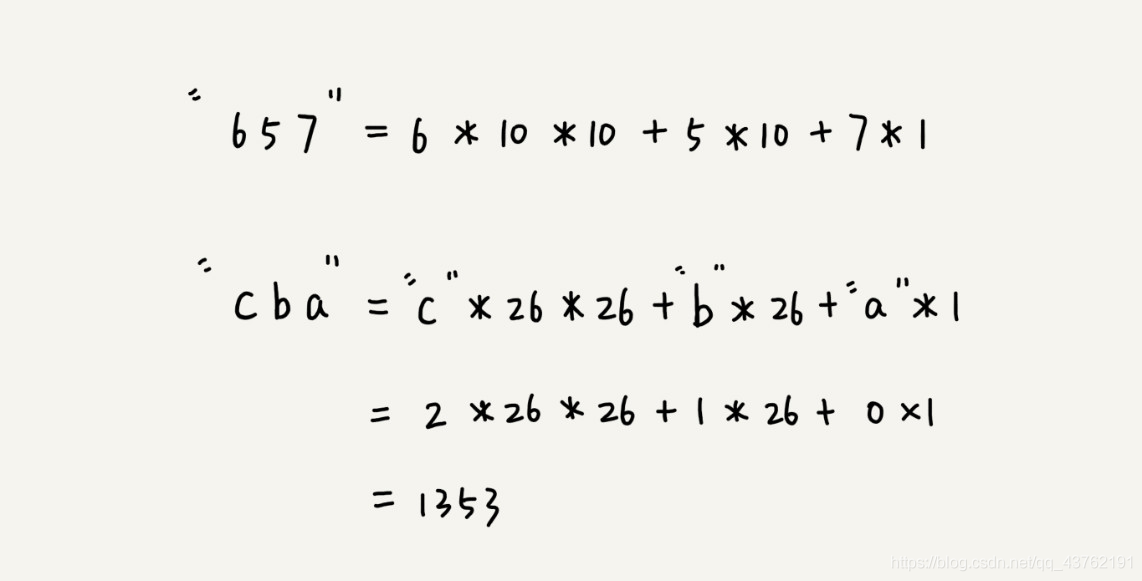
这里有一个小细节需要注意,那就是 26^(m-1) 这部分的计算,我们可以通过查表的方法来提高效率。我们事先计算好 26^0、26^1、26^2……26^(m-1),并且存储在一个长度为 m 的数组中
模式串哈希值与每个子串哈希值之间的比较的时间复杂度是 O(1),总共需要比较 n-m+1 个子串的哈希值,所以,这部分的时间复杂度也是 O(n)。所以,RK 算法整体的时间复杂度就是 O(n)。
但是呢,还有一个很致命的问题,叫做数值过大。
以幂增的速度是非常快的,用不了多久int就hold不住了啊,那要怎么办?难道我们前面所做的努力都白费了?
其实不然。
比方说我们可以改乘为加,当我们匹配到一样的哈希值的时候,再打开子串进行比对,因为相加的话是会有哈西冲突的。
此外,我们还可以加点优化,一边对主串构建,一边对子串进行匹配,如果一样的话就不继续计算后面的hash了。
该省的时候就要省,该花的时候就要花。
编辑器中的全局替换方法:BM算法
用过吗?比方说要在我这篇博客里找出全部的“主串”这个词,有没有想过其底层的原理?
这是一个性能优于KMP的算法。
坏字符
BM 算法的匹配顺序比较特别,它是按照模式串下标从大到小的顺序,倒着匹配的。
我们从模式串的末尾往前倒着匹配,当我们发现某个字符没法匹配的时候。我们把这个没有匹配的字符叫作坏字符(主串中的字符)

这时候该如何操作呢?我们去子串中寻找这个坏字符,如果找到了,就让两个字符的位置对上,继续往后,如果没有找到,就将整个子串移动到坏字符后面。
很显然,这会儿没找到。
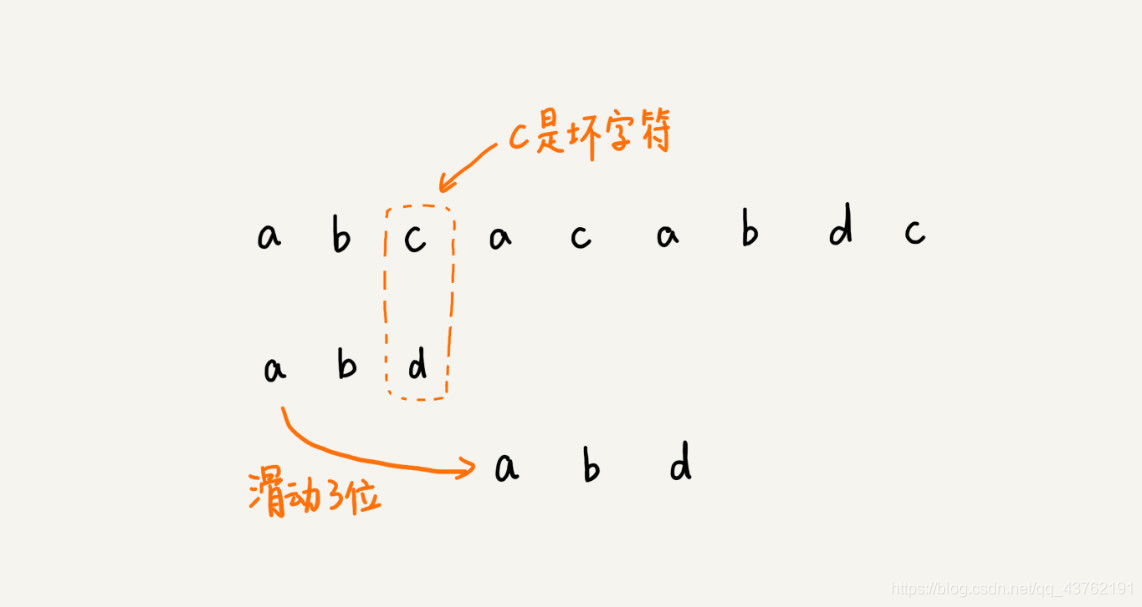
接下来该怎么滑呢?又是个坏字符。
但是在子串中找到了那个坏字符,那就将两个字符的位置对上。
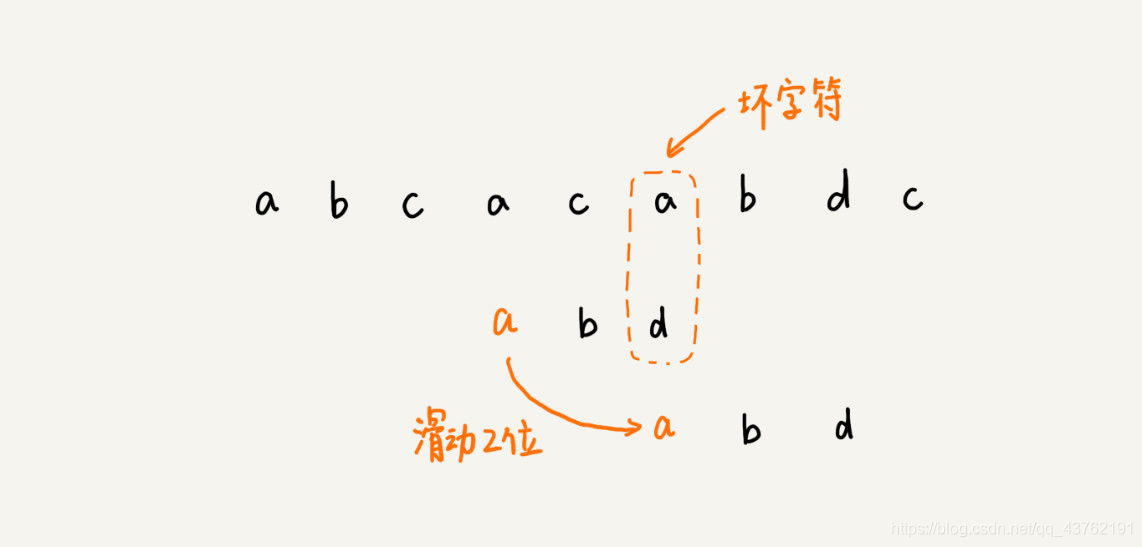
模式串中有对应的坏字符时,让模式串中 最靠右 的对应字符与坏字符相对。

但是呢,用这个规则还是不太够用的,有些个特殊情况吧,它会导致不但不会向后滑动模式串,还有可能会倒推、
比如说主串:kkkkkkkkkkkkkkkkkk,模式串是 akk
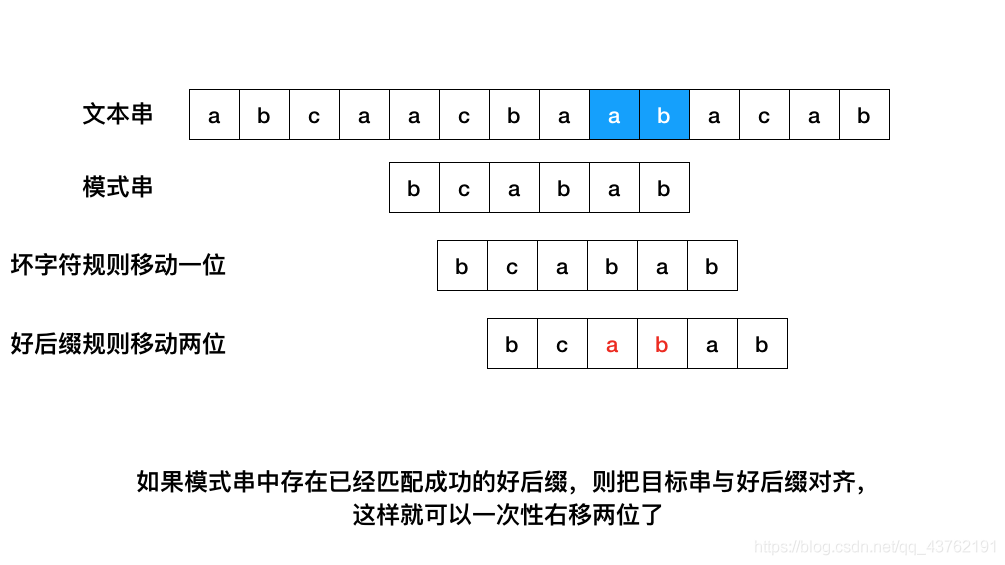
好后缀规则
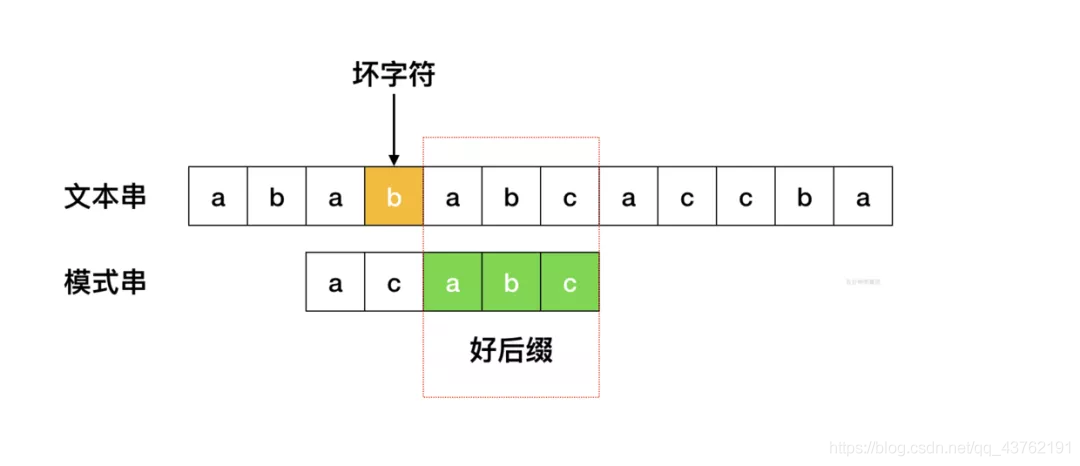
如果模式串中存在已经匹配成功的好后缀,则把目标串与好后缀对齐,然后从模式串的最尾元素开始往前匹配。
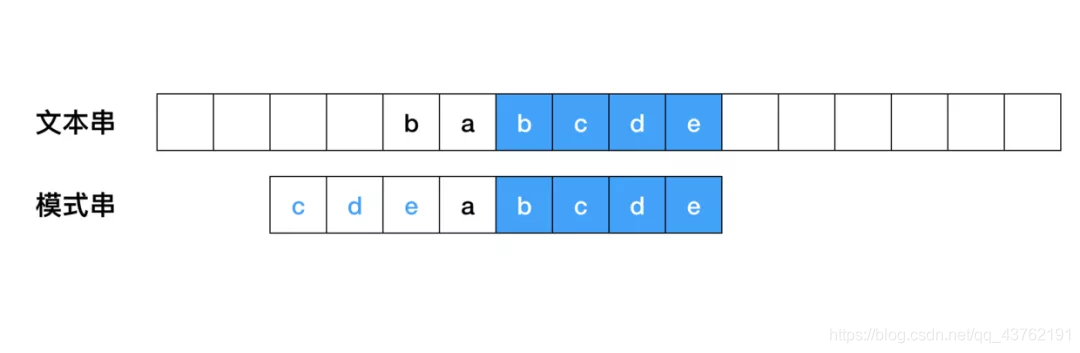
如果无法找到匹配好的后缀,找一个匹配的最长的前缀,让目标串与最长的前缀对齐:
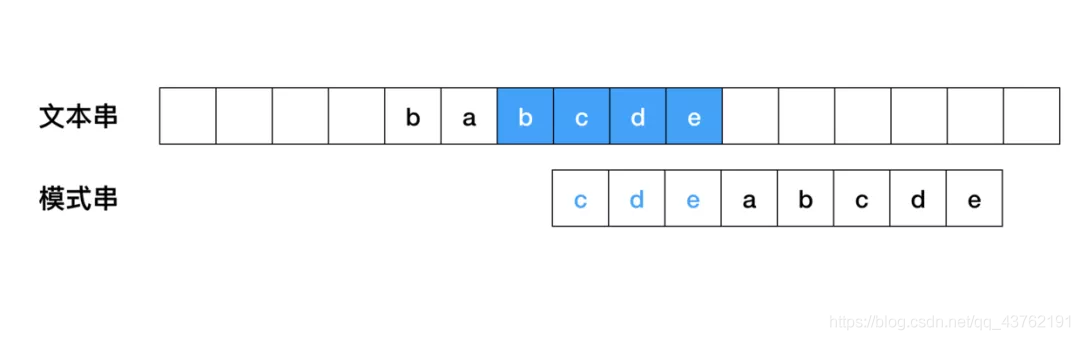
如果完全不存在和好后缀匹配的子串,则右移整个模式串
代码实现
难顶,我一定会回来的
// a,b 表示主串和模式串;n,m 表示主串和模式串的长度。
public int bm(char[] a, int n, char[] b, int m) {
int[] bc = new int[SIZE]; // 记录模式串中每个字符最后出现的位置
generateBC(b, m, bc); // 构建坏字符哈希表
int[] suffix = new int[m];
boolean[] prefix = new boolean[m];
generateGS(b, m, suffix, prefix);
int i = 0; // j 表示主串与模式串匹配的第一个字符
while (i <= n - m) { int j; for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配 if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是 j } if (j < 0) { return i; // 匹配成功,返回主串与模式串第一个匹配的字符的位置 } int x = j - bc[(int)a[i+j]]; int y = 0; if (j < m-1) { // 如果有好后缀的话 y = moveByGS(j, m, suffix, prefix); } i = i + Math.max(x, y);
}
return -1;
}
// j 表示坏字符对应的模式串中的字符下标 ; m 表示模式串长度
private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {
int k = m - 1 - j; // 好后缀长度
if (suffix[k] != -1) return j - suffix[k] +1;
for (int r = j+2; r <= m-1; ++r) { if (prefix[m-r] == true) { return r; }
}
return m;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
KMP算法
文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/118436310
