Leetcode 76最小覆盖子串&77组合&78子集

新人公众号(求支持)：bigsai 专注于Java、数据结构与算法，一起进大厂不迷路！
算法文章题解全部收录在github仓库bigsai-algorithm,求star！
关注回复进群即可加入力扣打卡群，欢迎划水。近期打卡：
LeetCode 67二进制求和&68文本左右对齐&69x的平方根
 LeetCode 70爬楼梯&71简化路径&72编辑距离(dp)
LeetCode 73矩阵置零&74搜素二维矩阵&75颜色分类
如有帮助，记得对本文一键三连！

LeetCode 76最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

示例 2：

输入：s = "a", t = "a"
输出："a"

提示：

1 <= s.length, t.length <= 105
s 和 t 由英文字母组成

进阶：你能设计一个在 o(n) 时间内解决此问题的算法吗？

问题分析：

题意很清晰，就是要求再s串中找到所有包含t串字符的短串。不考虑存储我们分析一下该怎么做呢？

常规思路：暴力枚举，一个字符串有左到右，我只需要从左向右遍历left，每个left找到最短的right覆盖t串即可。
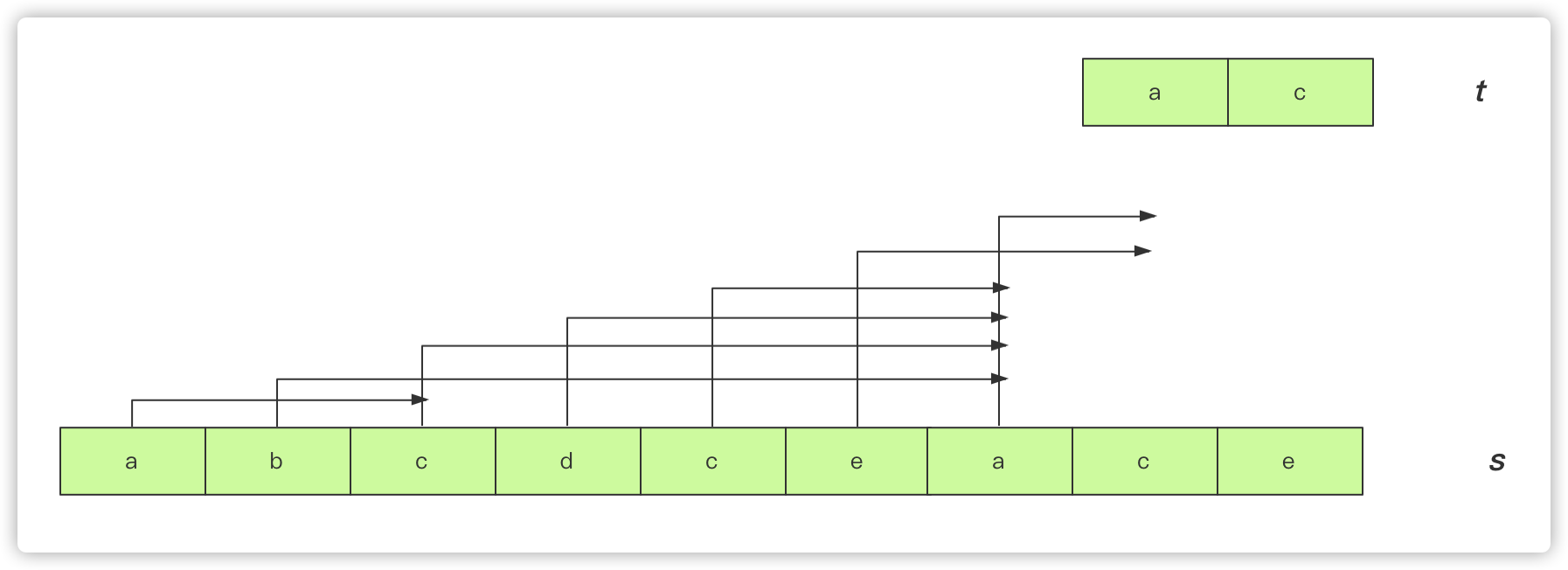
在这里插入图片描述

但是这样是一个O(n2)的操作，题目要求用O(n)来完成。该如何做呢？ 双指针
我们可以动态的去覆盖这个s串，在遍历的时候遵从一个策略：

选定left的时候，让right到达最短的那个能够覆盖的地方。
下一步将left右移的时候判断是否能够满足覆盖t串的条件，如果满足比较下是否需要更新结果，如果不满足那么将right向右一直找到能够覆盖为止。
重复上述一直到结束

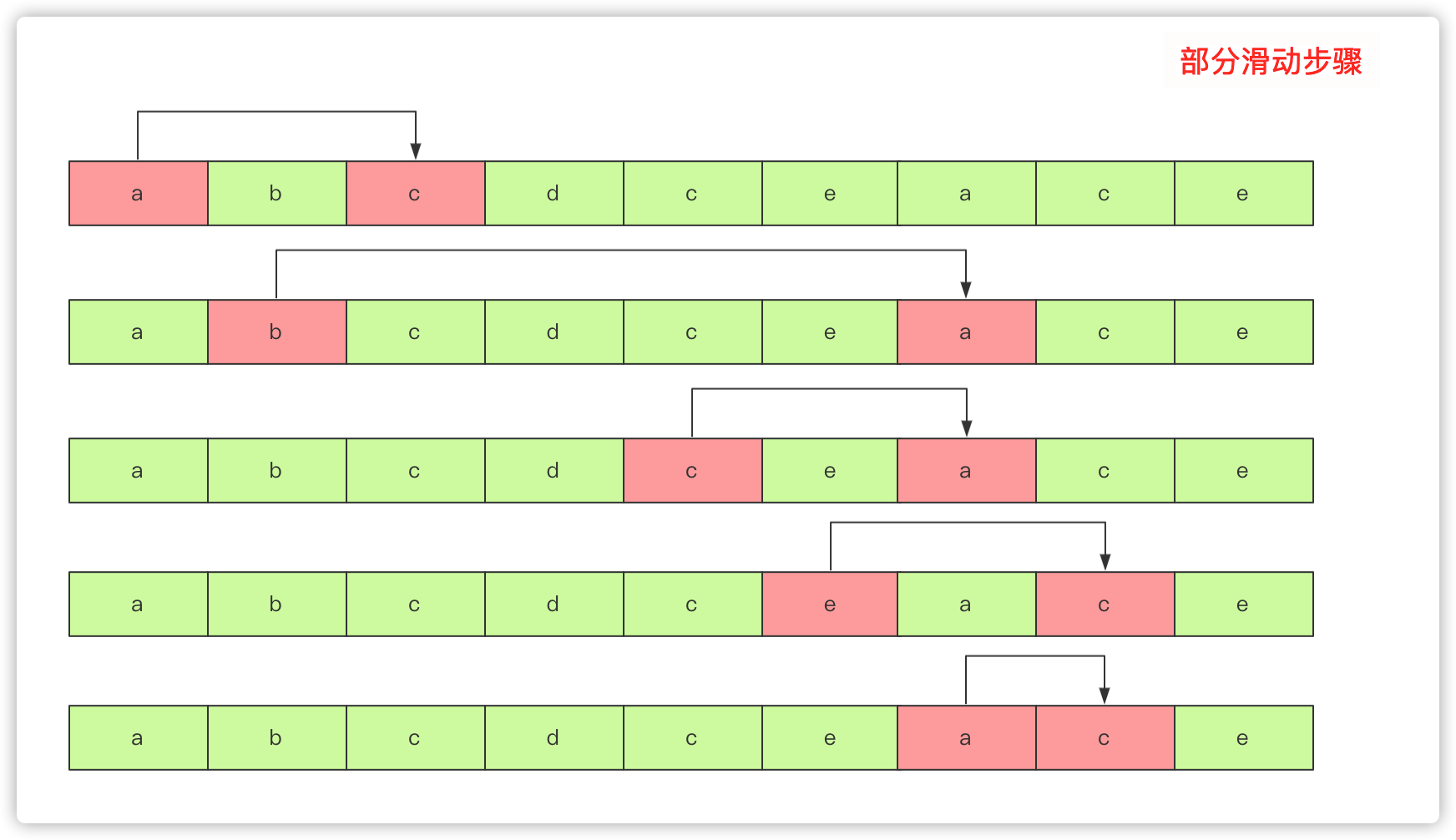
在这里插入图片描述

但是另一个需要你考虑得问题是，如何统计是否覆盖呢？
肯定是要通过某种容器，这里哈希肯定是最方便的了，但是我这里不用HashMap 使用2个int []数组分别统计s串和t串中字符出现的个数。

统计t串的可以开始就统计，统计s串的需要统计left和right范围内的字符。而可以借助一个int类型参数num来统计覆盖次数：也就是right向右遍历s串该字符如果比t串中次数少那么加一。如果left向右记录s串的字符减少如果小于t串中的字符数那么num减少。

具体实现的时候，将字符串转成字符数组，用左右区间标记替代每次字符串结果来优化时间，可以跑到3ms.
具体的代码为：

public String minWindow(String s, String t) { int countS[]=new int[150];//用来储存s中的字符
	int CountT[]=new int[150];//用来储存t中的字符 char strs[]=s.toCharArray();//转成数组更快
	char strt[]=t.toCharArray(); for(int i=0;i<strt.length;i++)
	{
		CountT[strt[i]]++;//计数
	}
	String value="";
	int num=0;//s中拥有t字符 的个数
	int valueLeft=0,valueRight=strs.length+1;//最终的左右区间范围
	int right=0;//right 临时指针
	for(int i=0;i<strs.length;i++)
	{ if(right==strs.length&&num<strt.length)//已经不可能了 推出
		{ break;
		}
		else if (num<strt.length) {//需要往右叠加 while (right<strs.length&&num<strt.length) { if(countS[strs[right]]++<CountT[strs[right]])//s这个字符数量小于t中这个字符的数量 { num++; } right++; }
		}
		//System.out.println("66666 "+right+" "+num);
		if(num<strt.length&&right==strs.length)//不满足条件 break;
		if(num==strt.length&&(valueRight-valueLeft>right-i))
		{ valueLeft=i; valueRight=right; } if(countS[s.charAt(i)]--<=CountT[s.charAt(i)])//左侧的left右移
		{ num--;
		} }
	if(valueRight!=strs.length+1)//如果有满足的字符串
	value=s.substring(valueLeft,valueRight);
	//System.out.println(value);
	return value; }

在这里插入图片描述

LeetCode 77组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

所有可能的k个数，经典回溯算法，要考虑两点：

k个数，可以通过一个数字类型来记录回溯到当前层的数字数量。
重复，避免 ab和ba的情况，对于重复的情况，可以借助一个下标只遍历下标后面的数字，就可以避免重复。

至于回溯算法的具体设计，老生常谈的问题这里就不作过多的复述啦。实现代码为：

public List<List<Integer>> combine(int n, int k) {
	List<List<Integer>> valueList=new ArrayList<List<Integer>>();
	int num[]=new int[n];
	boolean jud[]=new boolean[n];
	for(int i=0;i<n;i++)
	{
		num[i]=i+1;
	}

	List<Integer>team=new ArrayList<Integer>();
	dfs(num,-1,k,valueList,jud,n);
	return valueList; }
private void dfs(int[] num,int index, int count,List<List<Integer>> valueList,boolean jud[],int n) {
	if(count==0)
	{
		List<Integer>list=new ArrayList<Integer>();
		for(int i=0;i<n;i++)
		{ if (jud[i]) { list.add(i+1); }
		}
		valueList.add(list);
	}
	else {
		for(int i=index+1;i<n;i++)
		{ jud[i]=true; dfs(num, i, count-1, valueList,jud,n); jud[i]=false; }
	}
	
}

性能不算太差但有待优化。

LeetCode78 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

分析，和上面的思想差不多，不能重复的处理方式是一致的，但是元素个数的话就是在每次回溯的时候都要添加到结果集中。ps：List频繁插入删除效率并不高我使用boolean数组进行优化。

具体代码为

public List<List<Integer>> subsets(int[] nums) {
	List<List<Integer>> valueList=new ArrayList<List<Integer>>();
	boolean jud[]=new boolean[nums.length];
	List<Integer>team=new ArrayList<Integer>();
	dfs(nums,-1,valueList,jud);
	return valueList; }
private void dfs(int[] num,int index,List<List<Integer>> valueList,boolean jud[]) {
	{
		List<Integer>list=new ArrayList<Integer>();
		for(int i=0;i<num.length;i++)
		{ if (jud[i]) { list.add(num[i]); }
		}
		valueList.add(list);
	}
	{
		for(int i=index+1;i<num.length;i++)
		{ jud[i]=true; dfs(num, i, valueList,jud); jud[i]=false; }
	}
}

结语

原创不易，bigsai请你帮两件事帮忙一下:

star支持一下，您的肯定是我在平台创作的源源动力。
微信搜索「bigsai」，关注我的公众号，不仅免费送你电子书，我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode。

记得关注、咱们下次再见！

文章来源: bigsai.blog.csdn.net，作者：Big sai，版权归原作者所有，如需转载，请联系作者。

原文链接：bigsai.blog.csdn.net/article/details/110682620

（完）