
本来要拿《背包九讲》作为参考的,奈何太抽象,我看不懂
0-1背包问题
给你一个载重量为 W 的背包,以及一堆物品,这些物品都有属于自己的两个属性:价值var和质量wt,试问这个背包最多能装多少价值的物品。
这里面的每一个物品,要么装,要么不装。
看到这个图,第一反应是不是:性价比比一下。如果是这样想的朋友可以停下来了,性价比不行。
如果只有两个物品,一个4Kg,值8¥;一个15Kg,值10¥;很明显前面那个性价比高,但是显然我们要选的是后面这个。
这种题目,实在让人很懵逼,就好像千头万绪,但是所有思路都被自己给否定了。
动态规划标准套路
1、明确状态和选择
什么是状态,就是背包的容量,以及可以选择的物体。
什么是选择,这个物品,要不要放进背包。
2、明确dp数组
刚刚说到有两个状态,所以我们选用一个二维数组:dp[i][w]:对于前 i 个物体,在背包容量为w的时候,可以装的最大价值是dp[i][w]。
例:dp[3][5] = 6:对于前三个物体做选择,在背包容量为5的时候,可以选择的最大价值为6。
根据定义,我们的最终目标可以设为 dp[N][M],
base case 就是dp[0][···] = 0,dp[···][0] = 0,没有物品或者背包没有空间的时候,能装的最大价值就是0。
3、状态转移方程
对第i件物品来说,无非就是选中了,和没选中嘛。
那么,
如果选中了:d[i][w] = d[i-1][w-wt[i-1]]+var[i]
如果没选中:d[i][w] = d[i-1][w]
- 1
- 2
什么情况下要选?什么情况下不选呢?
那当然是哪个有利就选哪个嘛。
所以,伪代码怎么写?
伪代码
int dp[N+1][W+1]
dp[0][···] = 0
dp[···][0] = 0
for i in range(1,N):
for w in range(1,w):
dp[i][w] = max(装,不装) //装不装的状态转移已经在上面了
return dp[N][W]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
修缮代码
int knaspsack(int W,int N,vector<int>& wt,vector<int>& val){
vector<vector<int>> dp(N+1,vector<int>(W+1,0)); for(int i = 1;i <= N; i++){
for(int w = 1;w <= W; w++){ if(w-wt[i-1]<0) //没空间了 dp[i][w] = dp[i-1][w]; else dp[i][w] = max(d[i-1][w-wt[i-1]]+var[i],dp[i-1][w]);
}
}
return dp[N][W];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
子集背包问题
给你一个只包含正整数的数组,设计一个算法,将这个数组分为两个元素和相等的子集,如果能分,返回true,如果不能分,返回false。
这个问题怎么转化为背包为题呢?
首先,对这个数组计数,如果和是奇数,就返回-1吧,如果和是偶数,就除于二,记为n。
这个问题就转变为:从数组中找出一些数,使得它们的和恰好等于n。
其实看了这个题目,最直接的想法就是逆序排序之后用回溯
思路分析
状态和选择已经很明确了吧。
dp数组的含义嘛,dp[i][j] = x 表示,对于前 i 个物品,当前背包容量为 j 的时候,正好能将背包装满,则x为true,否则为false、
做一下状态压缩,把[i]去掉,反正i也是用来循环的。
如果不把 nums[i] 装入子集,则能够恰好装满背包,取决于上一个状态 dp[i-1][j],继承之前的结果。
如果把 nums[i] 装入子集,则能否恰好装满背包,取决于状态 dp[i-1][j-nums[i-1]]。
代码实现
bool canPartition(vector<int>& nums) { int sum = 0, n = nums.size(); for (int num : nums) sum += num; if (sum % 2 != 0) return false; sum = sum / 2; vector<bool> dp(sum + 1, false); // base case dp[0] = true; for (int i = 0; i < n; i++) for (int j = sum; j >= 0; j--) if (j - nums[i] >= 0) dp[j] = dp[j] || dp[j - nums[i]]; return dp[sum];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
完全背包问题
换零钱问题:给定不同面额的硬币(coins),和一个总金额(amount),写一个函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无数个。
说真的,我都快受不了了,是回溯不好用了吗?
来我画个图:
比方说现在,有1、2、5三种面值的硬币,总目标为10吧。
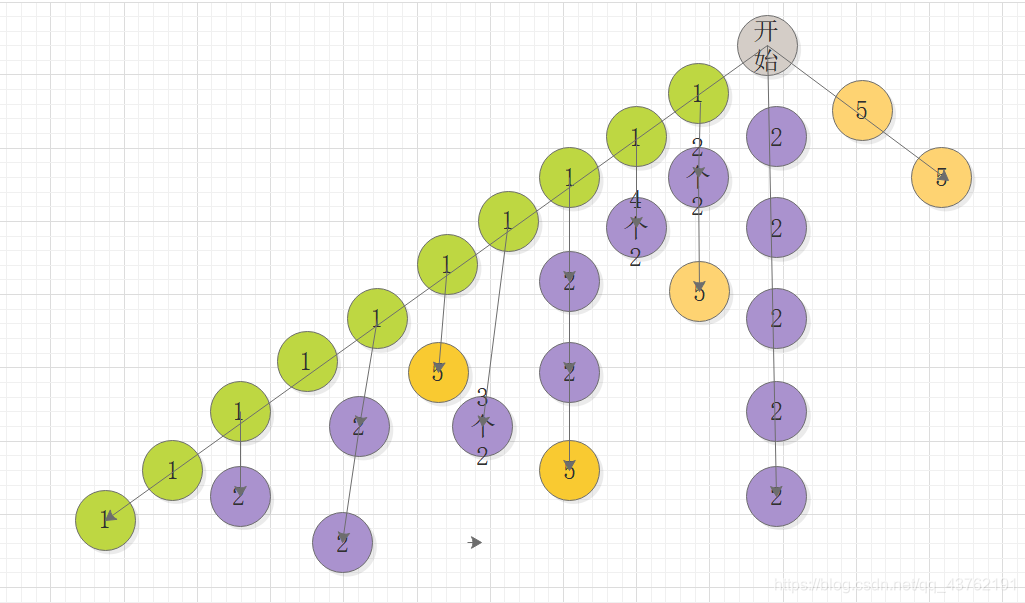
是吧,是回溯吧,这个我画的决策树可能是丑了点(我看得出来),将就着理解一下吧。
文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/113994053