【C++】算法集锦（3）：回溯，从入门到入土，七道试题精选、精讲、精练

在这里插入图片描述

前言

回溯算法，之前也是写过的，感觉还不错。但是之前分成两篇写了，现在重新整理一下，顺便我自己也回顾一下。

递归

要玩得转回溯算法，递归思想就要融入骨子里。
正好早上我整理了一篇递归相关的，不妨看一下：【C++】算法集锦（2）：递归

N叉树的遍历

我们从N叉树的遍历入手，来看一下回溯算法。

思考一下二叉树的回顾一下二叉树的遍历方式：

前序遍历 - 首先访问根节点，然后遍历左子树，最后遍历右子树；
中序遍历 - 首先遍历左子树，然后访问根节点，最后遍历右子树；
后序遍历 - 首先遍历左子树，然后遍历右子树，最后访问根节点；
层序遍历 - 按照从左到右的顺序，逐层遍历各个节点。

N 叉树的中序遍历没有标准定义，中序遍历只有在二叉树中有明确的定义。
我们跳过 N 叉树中序遍历的部分。

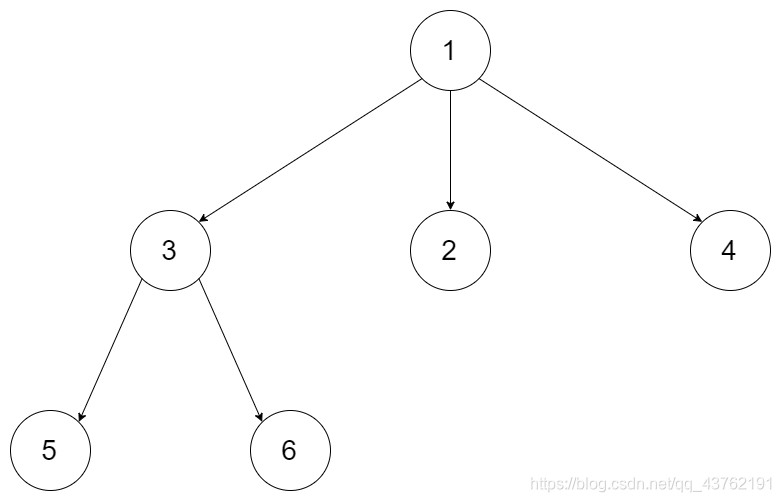
在这里插入图片描述

节点设计

class Node {
public: int val; vector<Node*> children;	//注意，这里不再是左右子节点了 Node() {} Node(int _val) { val = _val; } Node(int _val, vector<Node*> _children) { val = _val; children = _children; }
};

N叉树的前序遍历

给定一个 N 叉树，返回其节点值的前序遍历。

class Solution {
public: void preorderDFS(Node* root, int index, vector<int>& ret) { if (root == NULL) return; ret.push_back(root->val); int sz = (root->children).size(); while (index < sz) { preorderDFS(root->children[index], 0, ret);	//认真捋一下这一步 index += 1; } } vector<int> preorder(Node* root) { vector<int> ret; preorderDFS(root, 0, ret); return ret; }
};

后序遍历

给定一个 N 叉树，返回其节点值的后序遍历。


class Solution {
public: void postorderDFS(Node* root, int index, vector<int>& ret) { if (root == NULL) return; int sz = (root->children).size(); while (index < sz) { postorderDFS(root->children[index], 0, ret); index += 1; } ret.push_back(root->val); } vector<int> postorder(Node* root) { vector<int> ret; postorderDFS(root, 0, ret); return ret; }
};

层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

class Solution {
public: vector<vector<int>> result; void dfs(Node* root, int dep){ if(!root) return; if(dep == result.size()) result.emplace_back(); result[dep].push_back(root->val); auto children = root->children; for(auto ele:children){ dfs(ele, dep+1); } } vector<vector<int>> levelOrder(Node* root) { dfs(root, 0); return result; }
};

岛屿最大面积、八皇后问题、括号生成感觉比较简单，所以思路讲的就比较简陋，适合入门练手，建议看其他题目的讲解（全排列那题）。

回溯例题精讲

岛屿最大面积

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/max-area-of-island
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这题其实我自己做出来了，把它放在第一题嘛，我觉得因为它是比较简单的。
从头开始遍历，遇到“1”就展开上下左右搜索，搜空了就回溯，在搜索过程中计数，并将搜索到的位置全部置0，防止二次污染。

代码实现

int checkIsland(vector<vector<int>>& grid, int x, int y) { int count = 0; if (grid[x][y] == 0) return count; else { grid[x][y] = 0; count++; //上 if (x - 1 >= 0) count += checkIsland(grid, x - 1, y); //右 if ((y + 1) < grid[0].size()) count += checkIsland(grid, x, y + 1); //下 if ((x + 1) < grid.size()) count += checkIsland(grid, x + 1, y); //左 if ((y - 1) >= 0) count += checkIsland(grid, x, y - 1); } return count;
}

int maxAreaOfIsland(vector<vector<int>>& grid) { if (grid.size() == 0) return 0; int max = 0; for (int i = 0; i < grid.size(); i++) { for (int j = 0; j < grid[0].size(); j++) { int temp = checkIsland(grid, i, j); if (temp > max) max = temp; } } } return max;
}

八皇后问题

八皇后问题是一个古老的问题，于1848年由一位国际象棋棋手提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，如何求解？在这里插入图片描述

思路

将每一个棋子放在当前列的最前端，再放下一个棋子。
如果下一个棋子没地方放了，就回溯到前一个棋子，将其往后一个适宜位置挪动。
具体思路都在代码里了。

代码实现

#include<iostream>
using namespace std;

#define MAX_NUM 8		//皇后数量

int queen[MAX_NUM][MAX_NUM] = { 0 };

bool check(int x, int y) {	//检查一个坐标是否可以放置
	for (int i = 0; i < y; i++) {
		if (queen[x][i] == 1) {	//这一行是否可以存在 return false;
		}
		if (x - 1 - i > 0 && queen[x - 1 - i][y - 1 - i] == 1) {	//检查左斜列 return false;
		}
		if (x + 1 + i < MAX_NUM && queen[x + 1 + i][y + 1 + i] == 1) {	//检查右斜列 return false;
		}
	}
	queen[x][y] = 1;
	return true;
}

void showQueen() {
	for (int i = 0; i < MAX_NUM; i++) {
		for (int j = 0; j < MAX_NUM; j++) { cout << queen[i][j] << " ";
		}
		cout << endl;
	}
	cout << endl;
}

bool settleQueen(int x) {
	if (x == MAX_NUM) {	//遍历完毕，找到答案
		return true;
	}
	for (int i = 0; i < MAX_NUM; i++) {
		for (int y = 0; y < MAX_NUM; y++) { queen[y][x] = 0;	//清空当前列，省的回溯的时候被打扰
		}
		if (check(i,x)) {	//如果这行找着了 queen[i][x] = 1; showQueen();	//直观测试结果 if (settleQueen(x + 1)) {	//是时候往左了 return true;	//一路往左 }
		}
	}
	return false;	//如果不行，就退回来
}

括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

示例：

输入：n = 3
输出：[ "((()))", "(()())", "(())()", "()(())", "()()()" ]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/generate-parentheses
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

如果左括号数量不大于 n，我们可以放一个左括号。如果右括号数量小于左括号的数量，我们可以放一个右括号。

代码实现

vector<string> generateParenthesis(int n) { vector<string> res; generateParenthesisDFS(n, n, "", res); return res;
}
void generateParenthesisDFS(int left, int right, string out, vector<string> &res) { if (left > right) return; if (left == 0 && right == 0) res.push_back(out); else { if (left > 0) generateParenthesisDFS(left - 1, right, out + '(', res); if (right > 0) generateParenthesisDFS(left, right - 1, out + ')', res); }
}

全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/permutations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

怎么用，是不是感觉千头万绪，但是又捋不出一个头绪来，很难受。

思路

“全排列”就是一个非常经典的“回溯”算法的应用。我们知道，N 个数字的全排列一共有 N! 这么多个。

大家可以尝试一下在纸上写 3 个数字、4 个数字、5 个数字的全排列，相信不难找到这样的方法。

以数组 [1, 2, 3] 的全排列为例。

我们先写以 1 开头的全排列，它们是：[1, 2, 3], [1, 3, 2]；
再写以 2 开头的全排列，它们是：[2, 1, 3], [2, 3, 1]；
最后写以 3 开头的全排列，它们是：[3, 1, 2], [3, 2, 1]。

我们只需要按顺序枚举每一位可能出现的情况，已经选择的数字在接下来要确定的数字中不能出现。按照这种策略选取就能够做到不重不漏，把可能的全排列都枚举出来。

在枚举第一位的时候，有 3 种情况。
在枚举第二位的时候，前面已经出现过的数字就不能再被选取了；
在枚举第三位的时候，前面 2 个已经选择过的数字就不能再被选取了。

使用编程的方法得到全排列，就是在这样的一个树形结构中进行编程，具体来说，就是执行一次深度优先遍历，从树的根结点到叶子结点形成的路径就是一个全排列。

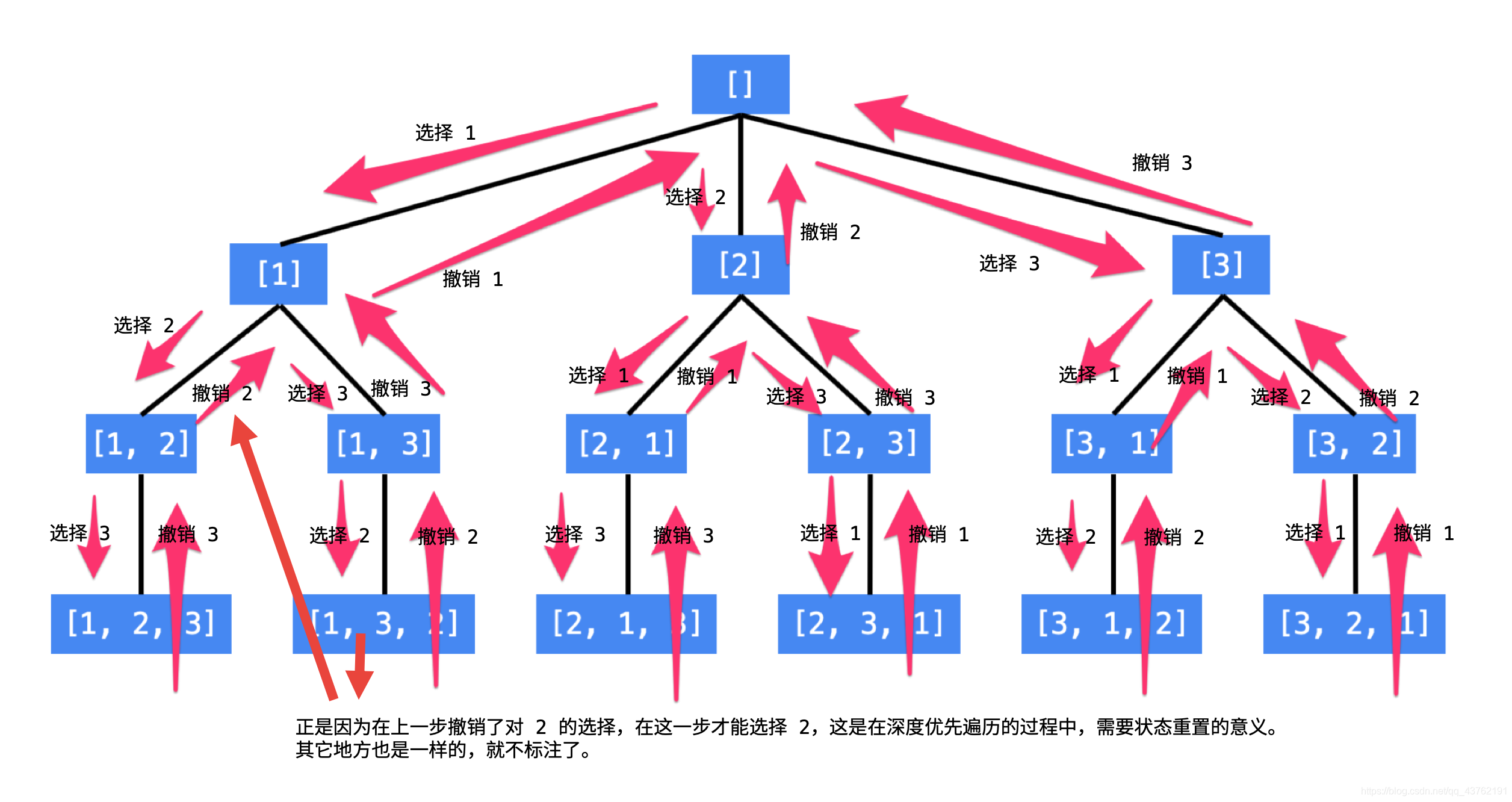
在这里插入图片描述

说明：

1、每一个结点表示了“全排列”问题求解的不同阶段，这些阶段通过变量的“不同的值”体现；
2、这些变量的不同的值，也称之为“状态”；
3、使用深度优先遍历有“回头”的过程，在“回头”以后，状态变量需要设置成为和先前一样；
4、因此在回到上一层结点的过程中，需要撤销上一次选择，这个操作也称之为“状态重置”；
5、深度优先遍历，可以直接借助系统栈空间，为我们保存所需要的状态变量，在编码中只需要注意遍历到相应的结点的时候，状态变量的值是正确的，具体的做法是：往下走一层的时候，path 变量在尾部追加，而往回走的时候，需要撤销上一次的选择，也是在尾部操作，因此 path 变量是一个栈。
6、深度优先遍历通过“回溯”操作，实现了全局使用一份状态变量的效果。

下面我们解释如何编码：

1、首先这棵树除了根结点和叶子结点以外，每一个结点做的事情其实是一样的，即在已经选了一些数的前提，我们需要在剩下还没有选择的数中按照顺序依次选择一个数，这显然是一个递归结构；

2、递归的终止条件是，数已经选够了，因此我们需要一个变量来表示当前递归到第几层，我们把这个变量叫做 depth；

3、这些结点实际上表示了搜索（查找）全排列问题的不同阶段，为了区分这些不同阶段，我们就需要一些变量来记录为了得到一个全排列，程序进行到哪一步了，在这里我们需要两个变量：
（1）已经选了哪些数，到叶子结点时候，这些已经选择的数就构成了一个全排列；
（2）一个布尔数组 used，初始化的时候都为 false 表示这些数还没有被选择，当我们选定一个数的时候，就将这个数组的相应位置设置为 true ，这样在考虑下一个位置的时候，就能够以 O(1) 的时间复杂度判断这个数是否被选择过，这是一种“以空间换时间”的思想。

我们把这两个变量称之为“状态变量”，它们表示了我们在求解一个问题的时候所处的阶段。

4、在非叶子结点处，产生不同的分支，这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。

5、另外，因为是执行深度优先遍历，从较深层的结点返回到较浅层结点的时候，需要做“状态重置”，即“回到过去”、“恢复现场”，我们举一个例子。

从 [1, 2, 3] 到 [1, 3, 2] ，深度优先遍历是这样做的，从 [1, 2, 3] 回到 [1, 2] 的时候，需要撤销刚刚已经选择的数 3，因为在这一层只有一个数 3 我们已经尝试过了，因此程序回到上一层，需要撤销对 2 的选择，好让后面的程序知道，选择 3 了以后还能够选择 2。

这种在遍历的过程中，从深层结点回到浅层结点的过程中所做的操作就叫“回溯”。

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/
来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码实现

vector<vector<int>> permute(vector<int>& nums) { if(nums.empty()) return {}; // 存放最后结果 vector<vector<int>> ans; // 存放某一个排列 vector<int> temp; // 判断该数字是否被使用过 vector<bool> used(nums.size(),false); // 进行递归求解 dfs(ans,temp,used,nums); return ans;
}

void dfs(vector<vector<int>>& ans,vector<int>& temp,vector<bool>& used, const vector<int>& nums)
{ // 如果当前排列数组的长度等于输入数组的长度 // 该排列已完成 // 将该排列的加入结果中，返回 if(temp.size()==nums.size()) { ans.push_back(temp); return; } // 循环的进行枚举所有状态 for(int i=0;i<nums.size();++i) { // 该数字已经选择过，跳过 if(used.at(i)) continue; // 选择当前数字 temp.push_back(nums.at(i)); // 记录该数字已被选择 used.at(i)=true; // 递归选择下一个数字 dfs(ans,temp,used,nums); // 回溯，撤销当前选择 used.at(i)=false; temp.pop_back(); }
}

再说两句

1、为什么使用深度优先遍历？

（1）首先是正确性，只有遍历状态空间，才能得到所有符合条件的解；

（2）在深度优先遍历的时候，不同状态之间的切换很容易，可以再看一下上面有很多箭头的那张图，每两个状态之间的差别只有 1 处，因此回退非常方便，这样全局才能使用一份状态变量完成搜索；

（3）如果使用广度优先遍历，从浅层转到深层，状态的变化就很大，此时我们不得不在每一个状态都新建变量去保存它，从性能来说是不划算的；

（4）如果使用广度优先遍历就得使用队列，然后编写结点类。使用深度优先遍历，我们是直接使用了系统栈，系统栈帮助我们保存了每一个结点的状态信息。于是我们不用编写结点类，不必手动编写栈完成深度优先遍历。大家可以尝试使用广度优先遍历实现一下，就能体会到这一点。

2、不回溯可不可以？

可以。搜索问题的状态空间一般很大，如果每一个状态都去创建新的变量，时间复杂度是 O(N)。在候选数比较多的时候，在非叶子结点上创建新的状态变量的性能消耗就很严重。

就本题而言，只需要叶子结点的那个状态，在叶子结点执行拷贝，时间复杂度是 O(N)。路径变量在深度优先遍历的时候，结点之间的转换只需要 O(1)。

最后，由于回溯算法的时间复杂度很高，因此，如果在遍历的时候，如果能够提前知道这一条分支不能搜索到满意的结果，就可以提前结束，这一步操作称之为剪枝。

回溯算法会大量应用“剪枝”技巧达到以加快搜索速度。有些时候，需要做一些预处理工作（例如排序）才能达到剪枝的目的。预处理工作虽然也消耗时间，但一般而且能够剪枝节约的时间更多。还有正是因为回溯问题本身时间复杂度就很高，所以能用空间换时间就尽量使用空间。否则时间消耗又上去了。

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/
来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

解回溯题的一般步骤

第 1 步都是先画图，画图是非常重要的，只有画图才能帮助我们想清楚递归结构，想清楚如何剪枝。就拿题目中的示例，想一想人手动操作是怎么做的，一般这样下来，这棵递归树都不难画出。

即在画图的过程中思考清楚：
1、分支如何产生；
2、题目需要的解在哪里？是在叶子结点、还是在非叶子结点、还是在从跟结点到叶子结点的路径？
3、哪些搜索是会产生不需要的解的？例如：产生重复是什么原因，如果在浅层就知道这个分支不能产生需要的结果，应该提前剪枝，剪枝的条件是什么，代码怎么写？

在这里插入图片描述

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/
来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

在这里插入图片描述
示例:

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明:
尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

在前面的一些步骤做出一些修改，并重新尝试找到可行解。

给出如下回溯函数 backtrack(combination, next_digits) ，它将一个目前已经产生的组合 combination 和接下来准备要输入的数字 next_digits 作为参数。

如果没有更多的数字需要被输入，那意味着当前的组合已经产生好了。
如果还有数字需要被输入：
遍历下一个数字所对应的所有映射的字母。
将当前的字母添加到组合最后，也就是 combination = combination + letter 。
重复这个过程，输入剩下的数字： backtrack(combination + letter, next_digits[1:]) 。

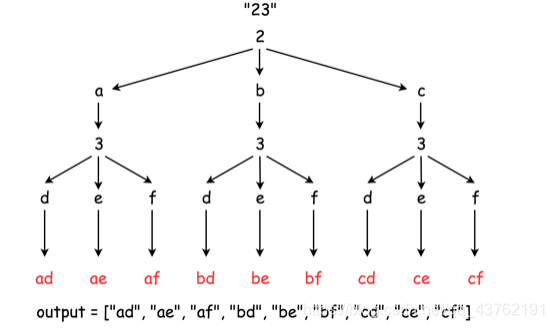
在这里插入图片描述

代码实现

其实代码里的备注还更加全全面

 //1. 用map记录每个数字按键对应的所有字母 map<char, string> M = { {'2', "abc"}, {'3', "def"}, {'4', "ghi"}, {'5', "jkl"}, {'6', "mno"}, {'7', "pqrs"}, {'8', "tuv"}, {'9', "wxyz"} }; //2. 存储最终结果和临时结果的变量 vector<string> ans; string current; //3. DFS函数，index是生成临时结果字串的下标， //每一个digits[index]数字对应临时结果current[index]的一位字母 void DFS(int index, string digits) { //出口 if(index == digits.size()) { ans.push_back(current); return; } //递归调用 //对于当前输入的第index号数字(digits[index])， //枚举其对应的所有字母(M[digits[index]][i]) for(int i = 0; i < M[digits[index]].size(); i++) { current.push_back(M[digits[index]][i]); //临时结果压入一个字母 DFS(index + 1, digits); //以在当前位置压入该字母这一“情况”为前提，构造此“分支”的后续结果 current.pop_back(); //状态还原，例如临时结果从 "ab" -> "a"，下一次循环尝试"ac"  } } vector<string> letterCombinations(string digits) { if(digits.size() == 0) { return ans; } DFS(0, digits); return ans; }

子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/subsets
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

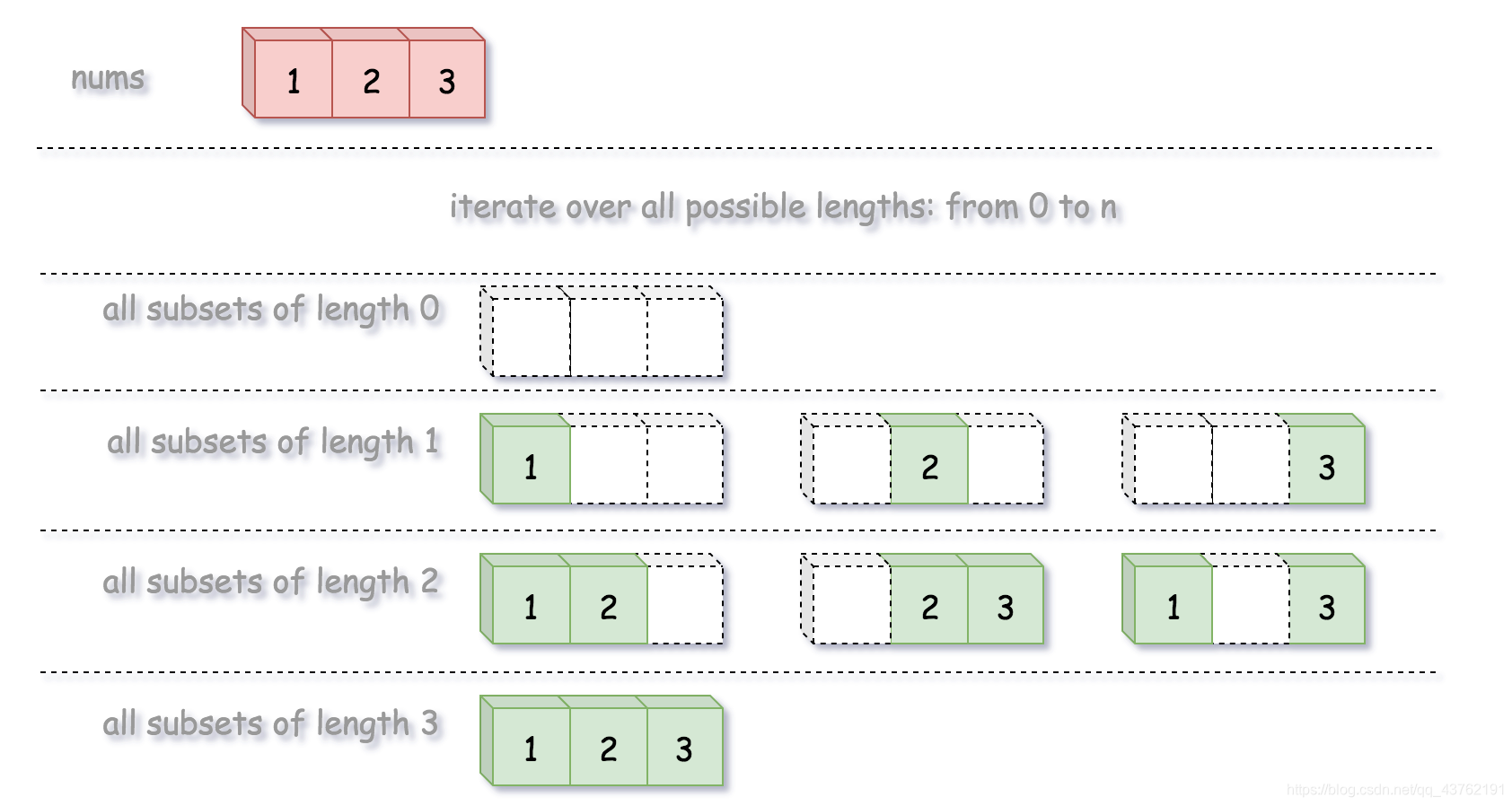
在这里插入图片描述
定义一个回溯方法 backtrack(first, curr)，第一个参数为索引 first，第二个参数为当前子集 curr。

如果当前子集构造完成，将它添加到输出集合中。

否则，从 first 到 n 遍历索引 i。 将整数 nums[i] 添加到当前子集 curr。 继续向子集中添加整数：backtrack(i + 1, curr)。 从 curr 中删除 nums[i] 进行回溯。

代码实现

class Solution {
private: vector<vector<int>> ret; vector<int> temp;
public: void DFS(vector<int>& nums,int pre,int level) { //退出条件：前面插入的是数组中最后一个元素 if (pre == nums.back()) { temp.clear(); return; } for (int i = 0; i < nums.size(); i++) { if (nums[i] <= pre) continue; temp.push_back(nums[i]); ret.push_back(temp); DFS(nums, nums[i],i+1); if (level) return; } } vector<vector<int>> subsets(vector<int>& nums) { ret.push_back({}); if (nums.empty()) return ret; DFS(nums, INT_MIN,0); return ret; }
};

到这儿到这儿，烧脑啊。。

文章来源: lion-wu.blog.csdn.net，作者：看，未来，版权归原作者所有，如需转载，请联系作者。

原文链接：lion-wu.blog.csdn.net/article/details/113862980

（完）

文章目录

前言

递归

N叉树的遍历

节点设计

N叉树的前序遍历

后序遍历

层序遍历

回溯例题精讲

岛屿最大面积

思路

代码实现

八皇后问题

思路

代码实现

括号生成

思路

代码实现

全排列

思路

代码实现

再说两句

解回溯题的一般步骤

电话号码的字母组合

思路

代码实现

子集

思路

代码实现