二叉树的递归与非递归遍历详解

二叉树是数组结构中非常重要的一种数据类型，很多数据结构与算法都是基于二叉树来进行扩展的，比如树，图等。而数据结构最重要的功能无非就是增删改查等操作，所以本篇文章主要来说说二叉树的查找怎么查找，完整代码可在我的github上查看。

本文中的左子节点和右子节点等同于左节点和右节点。

遍历形式

对于二叉树来说，比较重要的有三种遍历方式：

先序遍历：按照中间节点、左子树然后右子树的顺序遍历
中序遍历：按照左子树、中间节点然后右子树的顺序遍历
后序遍历：按照左子树、右子树然后中间节点的顺序遍历

可以看出这三种遍历的命名其实是根据中间节点的访问时机来命名的，然后这边再补充一种遍历方式–层序遍历，层序遍历就是从根节点开始，从上往下，从左往右进行遍历，按个人理解来说，层序遍历就是二叉树的广度优先搜索，先序遍历就是二叉树的深度优先搜索。

图解先、中、后序遍历

我们先来看看最容易理解的先序遍历是如何运行的，如下图：

上面说到先序遍历就是按照中间节点、左子树然后右子树的顺序遍历，所以从根节点，也就是图中的节点1，然后是节点1的左子树的根节点，也就是节点2，对于节点2来说，也是中左右的顺序遍历，所以节点2访问完以后就访问其左子树的根节点4，而4是叶子节点，没有子节点，则访问完节点4后，退回节点2访问节点2的右子树的根节点也就是5，访问完节点5后，同样因为节点5没有子节点，退回节点2，因为节点2的左右子树都已经访问过了，所以退回到节点1，访问节点1的右子树。以此类推，最后得到的访问顺序就是：1245367。

中序遍历运行过程如下图：

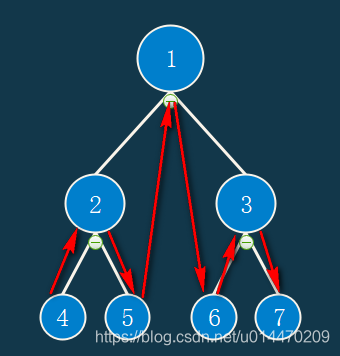
中序遍历是按照左子树、中间节点然后右子树的顺序遍历的，从根节点1开始，先寻找左子树根节点2，对于根节点2来说也同样需要先寻找其左子树的根节点也就是节点4。而节点4是叶子节点，无子节点，所以节点4就是这颗二叉树中序遍历的起点。也就是中序遍历的起始点是从根节点一直往左子树找到的第一个叶子节点（这句话不严谨，如果没有节点4，则是从节点2开始，但是这样更方便理解，而且这种情况下可以把节点4看成一个空节点）。那么剩下的过程和先序遍历类似，所得出的遍历顺序是：4251637。

后序遍历运行过程如下图：

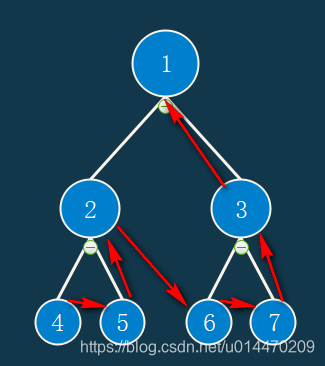
后序遍历是按照左子树、右子树然后中间节点的顺序遍历，和中序遍历一样，先一直往左找到底，如果能找到叶子节点的话，就从该节点开始，如上图就是节点4。但是不同的是，如果没有节点4的话，那么就从节点5继续往左找，当然因为这个图中节点5是叶子节点，所以节点5就是起始节点（没有节点4的话）。那么上面的二叉树的后序遍历的顺序就是：4526731。

后序遍历的过程理解起来比较绕了点，需要稍微多花点时间理解理解。

递归实现先、中、后序遍历

递归实现先、中、后序遍历是很简单的，不过递归在人脑中模拟起来相当费劲，所以最好的办法就是把下面的模板记住

traverse (root) { // 终止条件 if (!root) return /** 先序遍历 */ // console.log(root.val) // 遍历左子树 this.traverse(root.left) /** 中序遍历 */ // console.log(root.val) // 遍历右子树 this.traverse(root.right) /** 后序遍历 */ // console.log(root.val)
 }

从代码中，我们可以很清晰地看到，代码主要由三部分构成：

终止条件
对根节点进行相应的处理
递归遍历子树

而三种遍历的不同点在于对根节点进行处理的时机的不同。先序遍历是在依次遍历左右子树之前就对根节点进行处理；中序遍历是先遍历左子树，再对根节点进行处理，最后再遍历右子树；而后序遍历则是先依次遍历左右子树后再对根节点进行处理。

其实递归遍历代码很容易理解和记忆，但是其递归过程是一种机械式的运行过程，比较难以被人脑理解，所以一时间无法理解其递归过程的话，可以先记住该模板，而不去理解其过程。

非递归实现先、中、后序遍历

我们捋捋上面三种遍历的递归顺序会发现，三种遍历方式都是从根节点开始，往左子树遍历到底，然后返回父节点判断是否有右子树，再对右子树的根节点进行同样的操作。只是三种遍历方式的读取（处理）数据的时机不同罢了。先将左子树遍历到底，再从后面一个个搜索回来，这不就是典型的后进先出的顺序嘛，所以这里我们借助栈来实现三种遍历方式的非递归算法。
那么，如何使用栈来实现呢？首先创建一个栈，然后将根节点放入，然后依次将其左节点放入栈中，直到左节点为空。从栈中弹出一个节点，判断其是否有右节点，如果有右节点的话，将右节点放入栈中，然后依次将其左节点放入栈中，如此循环，直到栈为空，代码示意如下：

traverse_no_recursion (root) {
  // 这样声明是为了下面不做太多的初始判断
  var stack = [null]
  // 声明一个指向根节点的指针
  var p = root while (stack.length > 0) { // 将所有左节点放入stack中 while (p) { stack.push(p) p = p.left } p = stack.pop() // 弹出栈尾元素，将p指向其右节点（可能为null，所以先判断下） p = p && p.right
  } 

}

以上便是非递归的遍历模板，下面讲讲三种遍历方式的具体实现：

先序遍历：每次将节点放入栈之前，就读取（操作）值即可。
中序遍历：每次节点从栈中弹出之后，读取（操作）其值即可。
后序遍历：后序遍历稍微复杂点，但是只要脑子稍微绕下弯就会发现，在每次节点从栈中弹出之前，就直接读取其右节点压入栈中，这样右子树就会比跟节点先弹出来（后进先出），这样同样在节点从栈中弹出之后，读取（操作）其值即可。

先、中序遍历实现：

traverse_no_recursion (root) {
  var stack = [null]
  var p = root while (stack.length > 0) { // 将所有左节点放入stack中 while (p) { // 先序遍历 // console.log(p.val) stack.push(p) p = p.left } p = stack.pop() // 中序遍历 // console.log(p && p.val) p = p && p.right
  } 

}

后序遍历的思路实现：

traverse_no_recursion_LRD (root) {
  var stack = [null]
  var p = root while (stack.length > 0) { // 将所有左节点放入stack中 while (p) { stack.push(p) p = p.left } // 不弹出栈尾元素，直接读取其右节点 var lastNode = stack[stack.length - 1] if (lastNode && lastNode.right) { // 如果右节点存在，则将p指向右节点等待放入栈中 p = lastNode.right } else { // 如果右节点不存在，则节点开始出栈 var node = stack.pop() console.log(node.val) }
}

上面的程序运行你会发现报错，因为访问完右节点到底之后，弹出节点前又会判断右节点是否存在然后放入栈中，从而陷入死循环，所以这里我们需要加个处理，给节点添加一个是否访问过的标志（不想污染数据的话，可以使用hash表来记录访问过的节点），这个标志只会给访问过的右节点的父节点进行标记，代码如下：

traverse_no_recursion_LRD (root) {
  var stack = [null]
  var p = root while (stack.length > 0) { // 将所有左节点放入stack中 while (p) { stack.push(p) p = p.left } var lastNode = stack[stack.length - 1] if (lastNode && !lastNode.visited && lastNode.right) { p = lastNode.right // 这里添加一个已经访问过右子树的标志，不加标志的话，会在对右子树的访问陷入无限循环中 lastNode.visited = true } else { var node = stack.pop() console.log(node.val) }
  } 

}

层序遍历

层序遍历可以借助队列来实现，先将根节点放入队列中，然后进行出队列操作，判断出队列的节点是否有左右子节点，有的话，先左节点入队列，再右节点入队列，然后进行出队列操作，直到队列为空，由于队列先进先出的特点，左节点比右节点先进先出，那么左节点的子树也一样会比右节点的子树先进先出，也就是说，出队列的顺序就是层序遍历的顺序，代码如下：

traverse_level (root) { // 这里吧queue当成队列使用，入队列是push，出队列是shift var queue = [] queue.push(root) while (queue.length > 0) {
	//出队列 var root = queue.shift() // 输出root console.log(root.val) // 有左右子节点的话，依次放入 if (root.left) queue.push(root.left) if (root.right) queue.push(root.right) }
 }

上文也说了，层序遍历其实就是二叉树的广度优先搜索算法，所以很容易就可以类推出树的广度优先搜索算法，其实就是把左右子节点入队列换成将所有子节点入队列即可。同理，深度优先搜索算法和先序遍历其实是相同的。

二叉树的遍历十分重要，需要深刻理解并多加练习！

文章来源: blog.csdn.net，作者：sion诗音，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/u014470209/article/details/114809943

（完）