目录
一、题目内容
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
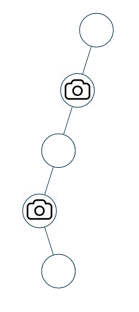
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。
二、解题思路
核心在于安装摄像头的条件:
1.安装摄像头的子节点的子节点为空
2.安装摄像头的子节点被该子节点的子节点监控了,该子节点不用再反过来监控其子节点,而是需要被其父节点监控安装摄像头
三、代码
-
# Definition for a binary tree node.
-
class TreeNode:
-
def __init__(self, x):
-
self.val = x
-
self.left = None
-
self.right = None
-
-
def __repr__(self):
-
return str(self.val)
-
-
class Solution:
-
def minCameraCover(self, root: TreeNode) -> int:
-
if not root:
-
return 0
-
self.ans = 0
-
-
-
def dfs(root):
-
"""
-
0:该结点附近有未被监视结点,安装监控器
-
1:该结点周围有监控器或该结点不存在,都不用安装监控器
-
2:该结点附近没有监控器,表示其附近需要监控器
-
"""
-
# 节点为空,标记为1
-
if not root:
-
return 1
-
left = dfs(root.left)
-
right = dfs(root.right)
-
# 第1情况:该节点的left或right(2)没有子节点(1),该节点标记为0,且安装摄像头
-
# 第2情况:该节点的left或right(2)的子节点(1)被该子节点的子节点(0)监控了,该节点标记为0,且安装摄像头
-
if left == 2 or right == 2:
-
self.ans += 1
-
return 0
-
# 该节点的left或right安装了监控器(0),不用安装监视器了,该节点标记为1
-
elif left == 0 or right == 0:
-
return 1
-
else:
-
# 该节点的子节点为空(1)
-
# 或该节点的子节点(1)被该子节点的子节点(0)监控了,该节点不用再反过来监控其子节点,而是只需要被其父节点监控, 控标记为2
-
return 2
-
# 就一个节点,没有子节点(1),则直接标记为2,那么就自己安装摄像头
-
if dfs(root) == 2:
-
self.ans += 1
-
return self.ans
-
-
-
-
if __name__ == '__main__':
-
a = TreeNode(0)
-
a.left = TreeNode(0)
-
a.left.left = TreeNode(0)
-
a.left.left.left = TreeNode(0)
-
a.left.left.left.right = TreeNode(0)
-
-
s = Solution()
-
ans = s.minCameraCover(a)
-
print(ans)
文章来源: nickhuang1996.blog.csdn.net,作者:悲恋花丶无心之人,版权归原作者所有,如需转载,请联系作者。
原文链接:nickhuang1996.blog.csdn.net/article/details/108725276