目录
一、题目内容
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。
(请注意,反斜杠字符是转义的,因此 \ 用 "\\" 表示。)。
返回区域的数目。
示例 1:
输入:
[
" /",
"/ "
]
输出:2
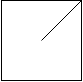
解释:2x2 网格如下:
示例 2:
输入:
[
" /",
" "
]
输出:1
解释:2x2 网格如下:
示例 3:
输入:
[
"\\/",
"/\\"
]
输出:4
解释:(回想一下,因为 \ 字符是转义的,所以 "\\/" 表示 \/,而 "/\\" 表示 /\。)
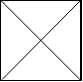
2x2 网格如下:
示例 4:
输入:
[
"/\\",
"\\/"
]
输出:5
解释:(回想一下,因为 \ 字符是转义的,所以 "/\\" 表示 /\,而 "\\/" 表示 \/。)
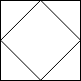
2x2 网格如下:
示例 5:
输入:
[
"//",
"/ "
]
输出:3
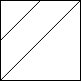
解释:2x2 网格如下:
提示:
1 <= grid.length == grid[0].length <= 30
grid[i][j] 是 '/'、'\'、或 ' '。
二、解题思路
三角形由三个边构成,那么三个点两两都连通则区域加1。
首先先将大格子的边上的点进行连通,然后再处理斜线‘/’上的点,连通则区域加1,不连通则将两个点进行连通,接着同样处理‘\',说白了就是三角形的顶点到达另一个顶点既可以直接通过相连的线段到达,也可以经过除二者之外的另一个顶点再到达。
总之连通就是这个意思~
三、代码
-
from collections import defaultdict
-
class Solution:
-
def regionsBySlashes(self, grid: list) -> int:
-
root = defaultdict(tuple)
-
-
def find(x):
-
if x != root[x]:
-
root[x] = find(root[x])
-
# return root[x]
-
return root[x]
-
-
# 检测x和y是否连通
-
def connected(x, y):
-
return find(x) == find(y)
-
-
# 连通x和y
-
def union(x, y):
-
if connected(x, y) is False:
-
root[find(x)] = find(y)
-
-
# 存储大格子所有点坐标
-
for i in range(len(grid) + 1):
-
for j in range(len(grid) + 1):
-
root[(i, j)] = (i, j)
-
-
# 左斜上三角的点进行连通
-
for i in range(len(grid) + 1):
-
union((0, 0), (0, i))
-
union((0, 0), (i, 0))
-
-
# 右斜下三角的点进行连通
-
for i in range(len(grid) + 1):
-
union((i, len(grid)), (len(grid), len(grid)))
-
union((len(grid), i), (len(grid), len(grid)))
-
-
# 这样大格子边上的点都进行了连通
-
-
res = 1 # 连通区域个数
-
-
for i in range(len(grid)):
-
for j in range(len(grid)):
-
if grid[i][j] == '/':
-
# 小格子的左下角和右上角之前已经连通了
-
if connected((i + 1, j), (i, j + 1)):
-
res += 1 # 个数加1
-
else:
-
# 否则小格子的左下角和右上角进行连通
-
union((i + 1, j), (i, j + 1))
-
-
elif grid[i][j] == '\\':
-
# 小格子的左上角和右下角之前已经连通了
-
if connected((i, j), (i + 1, j + 1)):
-
res += 1 # 个数加1
-
else:
-
# 否则小格子的左上角和右下角进行连通
-
union((i, j), (i + 1, j + 1))
-
-
return res
-
-
-
if __name__ == '__main__':
-
grid = [
-
"/\\",
-
"\\/"
-
]
-
s = Solution()
-
ans = s.regionsBySlashes(grid)
-
print(ans)
文章来源: nickhuang1996.blog.csdn.net,作者:悲恋花丶无心之人,版权归原作者所有,如需转载,请联系作者。
原文链接:nickhuang1996.blog.csdn.net/article/details/113104613