TEA系列算法学习
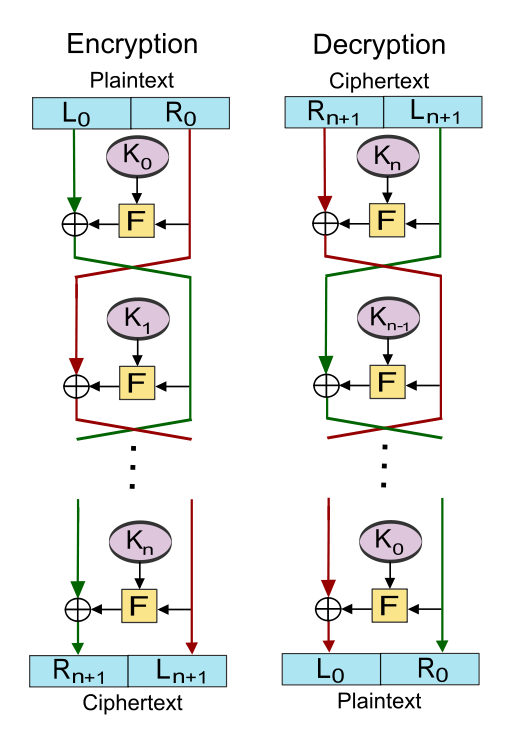
TEA(Tiny Encryption Algorithm)微型加密算法是一种易于描述的基于块的加密手法。通常来说,TEA加密算法会作用在两个32bit的无符号整数上(又或者可以理解成一个64bit的整数),并且会使用一个128bit的数字作为密钥。其拥有一个叫做Feistel 结构的密码学结构。这种密码学结构通俗的来讲就是会将加密的plaintext分成L、R两部分,并且满足 L_{i+1} = R_i, R_{i+1} = F(K_i,R_i) \oplus L_i 这种交换式的加密方式的一种结构。
TEA加密算法使用了64轮的加密算法结构,并且是成对的执行加密轮次。在加密周期中,每个密钥都是按照相同的轮次进行密钥的混合,从而完成加密。这个加密算法中为了防止基于轮询过程中的可能发生的攻击,使用了黄金分割律数字转换的一个数字 2654435769 (0x9E3779B9)作为魔数。
值得注意的是,TEA算法中的密钥中存在缺陷。每一个key都等效于其他算法中的三个key,这意味着实际上key中只有126bit会生效。因此,TEA算法的散列性能不好。这个弱点甚至导致了Xbox被黑客攻击。并且TEA容易受到密钥相关攻击,这需要在相关密钥对下选择
2^{23}个明文,并且具有 $2^{32}$ 的时间复杂度 ———— 摘自wiki,下文会解释
TEA算法实现
算法加密过程可以用一个图简单的说明:
输入一定要是一个64bit的数字,或者可以写作一个拥有两个元素的32bit的数组。,并且需要一个两倍长度的key(int[4])。整个加密流程如下:
void encrypt (uint32_t v[2], const uint32_t k[4]) {
uint32_t v0=v[0], v1=v[1], sum=0, i; /* set up */
uint32_t delta=0x9E3779B9; /* a key schedule constant */
uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */
for (i=0; i<32; i++) { /* basic cycle start */
sum += delta;
v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
} /* end cycle */
v[0]=v0; v[1]=v1;
}
有几个重要的特征
- 存在一个delta值,这个值会不停的增加到sum之中,形成一种循环的效果
- 传入的v0,v1会和传入的key0,key1运算。v1优先参与,并且会有一个位移->与密钥相加->异或的过程。
- v0 = 原先的v1值套用公式,v1 = 变化后的v0 套用公式
- 之前用于计算delta的sum状态值也会参与
由于是一个类似delta状态变化+异或加密的过程,所以整个流程反过来写即可得到解密
void decrypt (uint32_t v[2], const uint32_t k[4]) {
uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i; /* set up; sum is 32*delta */
uint32_t delta=0x9E3779B9; /* a key schedule constant */
uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */
for (i=0; i<32; i++) { /* basic cycle start */
v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
sum -= delta;
} /* end cycle */
v[0]=v0; v[1]=v1;
}
整个加密算法同样也适用于ECB,CBC等加密模式。
Davies–Meyer
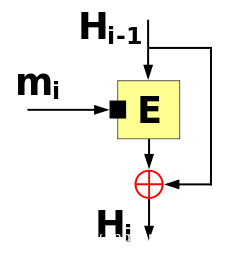
在密码学中,单向压缩函数(one-way compression function)是将两个固定长度的输入转换为固定长度的输出的功能。该转换是“单向”的,这意味着在给定输出的情况下,很难反向计算压缩前的输入。单向压缩函数与普通的数据压缩算法无关,而可以将其准确地(无损压缩)或近似(有损压缩)转换为原始数据。
单向要锁函数通常是由块加密算法变形而来的,一种常见的就是Davies–Meyer算法。该算法将消息的每个块(mi)作为加密算法的密钥。 它将上一次加密生成的哈希值(Hi-1)作为要加密的明文输入。 之后,将输出密文与上一个哈希值(Hi-1)进行异或(⊕),以产生下一个哈希值(Hi)。 在第一轮中,如果没有以前的哈希值,它将使用一个恒定的预先指定的初始值(H0),算法可以写成H_i = E_{m_i}(H_{i-1}) \oplus H_{i-1}
其中的E_{m_i}可以理解成使用mi块作为密钥的加密算法
TEA算法的弱点
TEA整个算法和密钥密切相关,这种算法我们称为密钥相关算法。这类算法如果密钥在加密过程中处理不当,很容易就会引发密钥相关攻击,感兴趣的可以看这边,具体的数学原理可以看这边,概括的说就是,TEA算法中的每一个密钥都会有其他三种相同的密钥。大致可用如下方式理解:
v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
v1那一段也同理。
上述的逻辑,我们可以简写成:V_0 = (C_1 + k_0) \oplus C_2 \oplus (C_2 + k_1)
其中C_*为常量。设此时我们让k0和k1的变化为\Delta k_*,变化后的我们写作k'_*,此时有公式:V'_0 = (C_1 + k'_0) \oplus C_2 \oplus (C_2 + k'_1)
如上,如果我们想要保证V'_0 == V_0,一个最好的办法就是让这个异或过程发生的变化被抵消掉。根据数学原理我们可以知道,如果将k0和k1的最高bit同时进行翻转,那么这个变化将会有1/2的概率被抵消
如果TEA算法被当作基于Davies–Meyer的hash算法的话,就很容易因为散列度不足导致碰撞发生。
在这边提到了关于TEA算法错误使用的例子。这里提到Xbox和Reiserfs都错误的使用了TEA算法,虽然xbox的源码我们找不到了,但是我找到了Reiserfs中使用TEA的源代码,其中关键的如下:
#define DELTA 0x9E3779B9
#define FULLROUNDS 10 /* 32 is overkill, 16 is strong crypto */
#define PARTROUNDS 6 /* 6 gets complete mixing */
/* a, b, c, d - data; h0, h1 - accumulated hash */
#define TEACORE(rounds) \
do { \
u32 sum = 0; \
int n = rounds; \
u32 b0, b1; \
\
b0 = h0; \
b1 = h1; \
\
do \
{ \
sum += DELTA; \
b0 += ((b1 << 4)+a) ^ (b1+sum) ^ ((b1 >> 5)+b); \
b1 += ((b0 << 4)+c) ^ (b0+sum) ^ ((b0 >> 5)+d); \
} while(--n); \
\
h0 += b0; \
h1 += b1; \
} while(0)
u32 keyed_hash(const signed char *msg, int len)
{
u32 k[] = { 0x9464a485, 0x542e1a94, 0x3e846bff, 0xb75bcfc3 };
u32 h0 = k[0], h1 = k[1];
u32 a, b, c, d;
u32 pad;
int i;
/* assert(len >= 0 && len < 256); */
pad = (u32) len | ((u32) len << 8);
pad |= pad << 16;
while (len >= 16) {
a = (u32) msg[0] |
(u32) msg[1] << 8 | (u32) msg[2] << 16 | (u32) msg[3] << 24;
b = (u32) msg[4] |
(u32) msg[5] << 8 | (u32) msg[6] << 16 | (u32) msg[7] << 24;
c = (u32) msg[8] |
(u32) msg[9] << 8 |
(u32) msg[10] << 16 | (u32) msg[11] << 24;
d = (u32) msg[12] |
(u32) msg[13] << 8 |
(u32) msg[14] << 16 | (u32) msg[15] << 24;
TEACORE(PARTROUNDS);
len -= 16;
msg += 16;
}
if (len >= 12) {
a = (u32) msg[0] |
(u32) msg[1] << 8 | (u32) msg[2] << 16 | (u32) msg[3] << 24;
b = (u32) msg[4] |
(u32) msg[5] << 8 | (u32) msg[6] << 16 | (u32) msg[7] << 24;
c = (u32) msg[8] |
(u32) msg[9] << 8 |
(u32) msg[10] << 16 | (u32) msg[11] << 24;
d = pad;
for (i = 12; i < len; i++) {
d <<= 8;
d |= msg[i];
}
} else if (len >= 8) {
a = (u32) msg[0] |
(u32) msg[1] << 8 | (u32) msg[2] << 16 | (u32) msg[3] << 24;
b = (u32) msg[4] |
(u32) msg[5] << 8 | (u32) msg[6] << 16 | (u32) msg[7] << 24;
c = d = pad;
for (i = 8; i < len; i++) {
c <<= 8;
c |= msg[i];
}
} else if (len >= 4) {
a = (u32) msg[0] |
(u32) msg[1] << 8 | (u32) msg[2] << 16 | (u32) msg[3] << 24;
b = c = d = pad;
for (i = 4; i < len; i++) {
b <<= 8;
b |= msg[i];
}
} else {
a = b = c = d = pad;
for (i = 0; i < len; i++) {
a <<= 8;
a |= msg[i];
}
}
TEACORE(FULLROUNDS);
/* return 0;*/
return h0 ^ h1;
}
可以看到,Reiserfs将输入作为了加密算法的密钥,然后调用TEA算法来进行hash。我们可以按照前文提到的攻击手段,给出如下的例子:
int main()
{
u_int32_t key[] = {1,2,3,4};
key[1] |= (1<<31);
printf("key0 = 0x%x\n",key[0]);
printf("key1 = 0x%x\n",key[1]);
printf("[1] wrong hash function get ans:%x\n", keyed_hash(key, 16));
key[0] |= (1<<31);
key[1] &= ((1<<31)-1);
printf("key0 = 0x%x\n",key[0]);
printf("key1 = 0x%x\n",key[1]);
printf("[2] wrong hash function get ans:%x\n", keyed_hash(key, 16));
return 0;
}
此时会发现,两个key会得出同样的hash值。Xbox当年就是因为错误的使用TEA作为hash函数,从而导致原先从ROM加载的bootloader地址被修改成从RAM加载,从而绕过了相关安全固件的检查,感兴趣的可以看这里(如果将来有空,可以帮忙翻译一下这类文章,感觉非常有的有趣)
XTEA
为了解决TEA算法中的密钥相关攻击,TEA的设计者提出了XTEA(eXtended TEA)算法来解决之前的密钥相关攻击问题。
#include <stdint.h>
/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;
for (i=0; i < num_rounds; i++) {
v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
sum += delta;
v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
}
v[0]=v0; v[1]=v1;
}
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;
for (i=0; i < num_rounds; i++) {
v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
sum -= delta;
v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
}
v[0]=v0; v[1]=v1;
}
可以看到相较之前,发生了如下的变化:
- 由之前的
((v1<<4) + k0) ^ ((v1>>5) + k1)变化成了((v1 << 4) ^ (v1 >> 5)) + v1),此时v1内部数据的加密变化不再受到密钥的影响。 - 原先的
v1 + sum变成了(sum + key[sum & 3])以及sum + key[(sum>>11) & 3],密钥变成了轮转使用,而不是固定只针对某种数据进行加密(解密)。并且此时密钥的选取受到sum的影响 -
sum += delta的时机由每次加密开头就发生变化到v0,v1两个block加密的中间。
这些变化帮助XTEA摆脱了一些密钥相关攻击,不过同时诞生了一种叫做TEA 块加密的加密手法。这种手法作用在一些可变长的数据中(XTEA默认用于64bit长的数据)。这中加密使用XTEA的轮转加密函数(就是上述的加密流程),但是却将同一段消息进行多次迭代加密。因为它对整个消息进行操作,所以块加密具有不需要ECB、CBC那些分组密码加密的属性。然而这个方式给XTEA本身引入了漏洞,如下
void teab1_encrypt(long *v, long n, long *k)
{
unsigned long z = v[n - 1], sum = 0, e;
long p, q;
for (q = 6 + 52 / n; q > 0; q--)
{
sum += 0x9e3779b9;
e = sum >> 2 & 3 ;
for (p = 0; p < n; p++)
z = v[p] += (((z << 4) ^ (z >> 5)) + z) ^
(k[(p & 3) ^ e] + sum);
}
}
这类加密算法本身虽然套用了XTEA,不过总的来说也是属于一种错误使用,所以给了暴力破解的可能。感兴趣的可以参考这里
XXTEA
在经历了块加密的问题之后,XTEA再度进化, 变成了支持块加密XXTEA。
这次的加密代码如下:
#include <stdint.h>
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))
void btea(uint32_t *v, int n, uint32_t const key[4]) {
uint32_t y, z, sum;
unsigned p, rounds, e;
if (n > 1) { /* Coding Part */
rounds = 6 + 52/n;
sum = 0;
z = v[n-1];
do {
sum += DELTA;
e = (sum >> 2) & 3;
for (p=0; p<n-1; p++) {
y = v[p+1];
z = v[p] += MX;
}
y = v[0];
z = v[n-1] += MX;
} while (--rounds);
} else if (n < -1) { /* Decoding Part */
n = -n;
rounds = 6 + 52/n;
sum = rounds*DELTA;
y = v[0];
do {
e = (sum >> 2) & 3;
for (p=n-1; p>0; p--) {
z = v[p-1];
y = v[p] -= MX;
}
z = v[n-1];
y = v[0] -= MX;
sum -= DELTA;
} while (--rounds);
}
}
可以看到是由之前提到过的块加密衍生的一种写法。并且作者给出了这种算法的优势:
- 每一个bit的更改将影响整个块的大约一半的bit位,但。
- 不用进行加密模式的选择。
- 即使采用始终更改发送的数据(可能只是一个消息号)的正确用法,只有相同的消息会给出相同的结果,并且只有很少量的信息泄漏。
- 应始终检查消息号,因为此操作是针对接受随机消息的检查。
- 应该无法被剪切和合并攻击。
- 如果不能接受很长的消息,则可以将它们分成60个单词的小块,并类似于用于DES的方法进行链接。
不过即使这样,这个算法似乎还是存在选择明文攻击的可能。感兴趣的可以自行搜索。
CTF题目中的常见TEA
这类算法比较常见于逆向中,在分析二进制文件中的算法的时候有几个识别的特征:
- 可能存在针对64bit以及128bit数字的操作(输入的msg和key)
- 存在先进行位移,然后异或的类似操作(
(z>>5^y<<2)这类混合变换) - 前面一个复杂的混合变换的结果可能会叠加到另一个值上,两者相互叠加(Feistel 结构)
- 获取密钥的时候,会使用某一个常量值作为下标(
key[(sum>>11) & 3]) - 会在算法开始定义一个delta,并且这个值不断的参与算法,但是从来不会受到输入的影响(delta数值,根据见过的题目中很少会直接使用0x9e3779b9)
解决逆向题大部分出现TEA的场合都是【识别算法->编写对应解密程序】,将上述的算法进行逆推即可得到解密。
实战:xnuca2020 babyarm
这个题目里面的TEA是出题人魔改过的:
if ( (signed int)v34 <= 15 )
{
v9 = v4[15];
v28 = v4[1];
v10 = v4[6];
v32 = *v4;
v11 = v4[9];
v25 = v4[2];
v12 = v4[10];
v29 = v4[3];
v13 = v4[11];
v26 = v4[4];
v14 = v4[12];
v27 = v4[5];
v15 = v4[13];
v30 = v4[7];
v16 = v4[14];
v33 = v4[15];
v31 = v4[8];
do
{
sum = 0;
do
{
sum -= 0x61C88647;
v32 += (((v28 >> 3) ^ 16 * v9) + (4 * v28 ^ (v9 >> 5))) ^ ((v9 ^ *(int *)((char *)&v40 + (sum & 0xC) - 0x14))// ((char *)&v41 + (v17 & 0xC) - 0x14)这种写法表示:(包括写成-20->0x14)+ (v28 ^ sum));
v28 += ((*(&v40 + (((unsigned __int8)(sum >> 2) ^ 1) & 3) - 5) ^ v32) + (v25 ^ sum)) ^ (((v25 >> 3) ^ 16 * v32)
+ (4 * v25 ^ (v32 >> 5)));
v25 += ((*(&v40 + (((unsigned __int8)(sum >> 2) ^ 2) & 3) - 5) ^ v28) + (v29 ^ sum)) ^ (((v29 >> 3) ^ 16 * v28)
+ (4 * v29 ^ (v28 >> 5)));
v29 += ((*(&v40 + (((unsigned __int8)(sum >> 2) ^ 3) & 3) - 5) ^ v25) + (v26 ^ sum)) ^ (((v26 >> 3) ^ 16 * v25)
+ (4 * v26 ^ (v25 >> 5)));
v26 += ((*(&v40 + ((sum >> 2) & 3) - 5) ^ v29) + (v27 ^ sum)) ^ (((v27 >> 3) ^ 16 * v29)// 没有异或
+ (4 * v27 ^ (v29 >> 5)));
v27 += ((*(&v40 + (((unsigned __int8)(sum >> 2) ^ 5) & 3) - 5) ^ v26) + (v10 ^ sum)) ^ (((v10 >> 3) ^ 16 * v26)
+ (4 * v10 ^ (v26 >> 5)));
v10 += ((*(&v40 + (((unsigned __int8)(sum >> 2) ^ 6) & 3) - 5) ^ v27) + (v30 ^ sum)) ^ (((v30 >> 3) ^ 16 * v27)
+ (4 * v30 ^ (v27 >> 5)));
v30 += ((*(&v40 + (((unsigned __int8)(sum >> 2) ^ 7) & 3) - 5) ^ v10) + (v31 ^ sum)) ^ (((v31 >> 3) ^ 16 * v10)
+ (4 * v31 ^ (v10 >> 5)));
v18 = v31
+ (((*(&v40 + ((sum >> 2) & 3) - 5) ^ v30) + (v11 ^ sum)) ^ (((v11 >> 3) ^ 16 * v30)// 没有异或
+ (4 * v11 ^ (v30 >> 5))));
v11 += ((*(&v40 + (((unsigned __int8)(sum >> 2) ^ 9) & 3) - 5) ^ v18) + (v12 ^ sum)) ^ (((v12 >> 3) ^ 16 * v18)
+ (4 * v12 ^ (v18 >> 5)));
v31 = v18;
LOBYTE(v18) = sum >> 2;
v12 += ((*(&v40 + (((unsigned __int8)v18 ^ 0xA) & 3) - 5) ^ v11) + (v13 ^ sum)) ^ (((v13 >> 3) ^ 16 * v11)
+ (4 * v13 ^ (v11 >> 5)));
v13 += ((*(&v40 + (((unsigned __int8)v18 ^ 0xB) & 3) - 5) ^ v12) + (v14 ^ sum)) ^ (((v14 >> 3) ^ 16 * v12)
+ (4 * v14 ^ (v12 >> 5)));
v14 += ((*(&v40 + ((sum >> 2) & 3) - 5) ^ v13) + (v15 ^ sum)) ^ (((v15 >> 3) ^ 16 * v13)// 没有异或
+ (4 * v15 ^ (v13 >> 5)));
v15 += (((v16 >> 3) ^ 16 * v14) + (4 * v16 ^ (v14 >> 5))) ^ ((*(&v40 + (((unsigned __int8)v18 ^ 0xD) & 3) - 5) ^ v14)
+ (v16 ^ sum));
v16 += (((v33 >> 3) ^ 16 * v15) + (4 * v33 ^ (v15 >> 5))) ^ ((*(&v40 + (((unsigned __int8)v18 ^ 0xE) & 3) - 5) ^ v15)
+ (v33 ^ sum));
v19 = (((v32 >> 3) ^ 16 * v16) + (4 * v32 ^ (v16 >> 5))) ^ ((*(&v40 + (((unsigned __int8)v18 ^ 0xF) & 3) - 5) ^ v16)
+ (v32 ^ sum));
*v4 = v32;
v4[1] = v28;
v4[2] = v25;
v4[3] = v29;
v4[4] = v26;
v4[5] = v27;
v9 = v19 + v33;
v4[7] = v30;
v4[6] = v10;
v4[8] = v31;
v4[9] = v11;
v4[10] = v12;
v4[11] = v13;
v4[12] = v14;
v4[13] = v15;
v4[14] = v16;
v4[15] = v19 + v33;
v33 += v19;
}
while ( sum != 0x8FF34781 );
++v34;
}
while ( v34 != (char *)16 );
出题人在这个算法前面的逻辑里玩了一个小花招:这段逻辑并不会一开始就出现在main函数中,而是在执行的时候,从.init_array取出的函数会将main函数的后方逻辑修改成这个函数的入口。整体逻辑比较偏长,不过可以辨认应该是魔改的XXTEA,并且每16个字节为一组进行的加密。这个题有几个小坑
- sum是减法而不是TEA算法中常见的加法运算
- 这几个加密算法中的4,8,12,16个字节的算法不同于其他的加密算法
不过识别出这些坑之后,由于我们知道TEA算法实际上是满足Feistel 结构的算法。这一类算法在已知key的情况下,必定是可以反推的。通过观察我们可以知道,v4[15]正好是最新的一个状态,所以可以从这个状态往回进行推理。题目中的key就藏在了文件中,于是最终解密代码我们可以写成:
uint32_t DeryptoLoop(unsigned int num1, unsigned int num2, uint32_t sum, uint32_t index)
{
unsigned int key[4] = { 2,2,3,4 };
//unsigned int key[4] = { 4,3,2,2 };
uint32_t tmp1 = ((num1 >> 3) ^ 16 * num2) + (4 * num1 ^ (num2 >> 5));
uint32_t tmp2 = (key[((sum >> 2) ^ index) & 3] ^ num2) + (num1 ^ sum);
return tmp1 ^ tmp2;
}
uint32_t DeryptoLoop2(unsigned int num1, unsigned int num2, uint32_t sum, uint32_t index)
{
unsigned int key[4] = { 2,2,3,4 };
//unsigned int key[4] = { 4,3,2,2 };
uint32_t tmp1 = ((num1 >> 3) ^ 16 * num2) + (4 * num1 ^ (num2 >> 5));
uint32_t tmp2 = (key[((sum >> 2)) & 3] ^ num2) + (num1 ^ sum);
return tmp1 ^ tmp2;
}
void decrypt2(unsigned dec_2[16])
{
unsigned int state[16];
unsigned int DELTA = 0x8FF34781;
unsigned int key[4] = { 2,2,3,4 };
int round = 0;
for (int i = 0; i < 16; i++)
{
state[i] = enc_2[i];
}
do {
int tmpd = DELTA;
do {
state[15] -= DeryptoLoop(state[0], state[14], tmpd, 15);
state[14] -= DeryptoLoop(state[15], state[13], tmpd, 14);
state[13] -= DeryptoLoop(state[14], state[12], tmpd, 13);
state[12] -= DeryptoLoop2(state[13], state[11], tmpd, 12);
state[11] -= DeryptoLoop(state[12], state[10], tmpd, 11);
state[10] -= DeryptoLoop(state[11], state[9], tmpd, 10);
state[9] -= DeryptoLoop(state[10], state[8], tmpd, 9);
state[8] -= DeryptoLoop2(state[9], state[7], tmpd, 8);
state[7] -= DeryptoLoop(state[8], state[6], tmpd, 7);
state[6] -= DeryptoLoop(state[7], state[5], tmpd, 6);
state[5] -= DeryptoLoop(state[6], state[4], tmpd, 5);
state[4] -= DeryptoLoop2(state[5], state[3], tmpd, 4);
state[3] -= DeryptoLoop(state[4], state[2], tmpd, 3);
state[2] -= DeryptoLoop(state[3], state[1], tmpd, 2);
state[1] -= DeryptoLoop(state[2], state[0], tmpd, 1);
state[0] -= DeryptoLoop2(state[1], state[15], tmpd, 0);
tmpd += 0x61C88647;
} while (tmpd != 0);
round += 1;
} while (round < 16);
for (int i = 0; i < 16; i++)
{
dec_2[i] = state[i];
}
}
总结
最初只是想作为一个笔记记录一下学习过程,然而后来发现TEA的演进过程十分有趣,于是便想将这个有趣的故事分享给大家。
算法也是一个不断演进的过程,从TEA,XTEA,即便是XXTEA依然也被提出存在选择明文攻击的可能。安全是一个不断攻防的过程,并且每一个方面都可能称为切入点,这点从Xbox被破解这件事情上也能看的出来。
参考链接
Wiki TEA
Wiki XTEA
Wiki XXTEA
Wiki-Tiny_Encryption_Algorithm
Xbox_Security_System_With_TEA_Hash