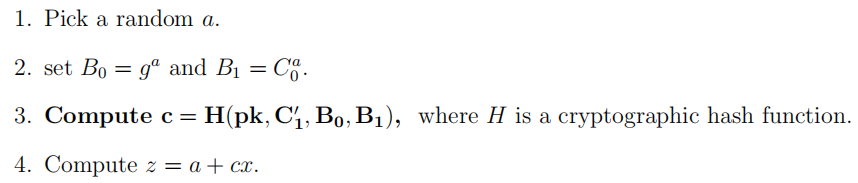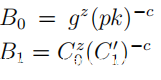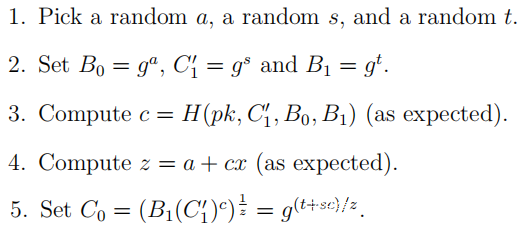瑞士邮政(SwissPost)-Scytl(在线投票公司)的投票系统中,实现Fiat-Shamir转换的弱点允许创建错误的解密证明,该证明可以完美验证,但实际上“证明”了与真实明文不同的解密。
例如,这可能欺骗解密服务用来将有效选票变成不会被计算在内的无效票。 如果攻击者知道哪些选票支持了它想要攻击的政党,则这种攻击可能会产生政治影响。
尽管从非形式化上看显然出了点问题,但形式化验证过程会通过。这与该投票系统应提供的完整可验证性相矛盾。如果错误地认为解密证明是正确的,那么漏洞利用似乎会使系统处于“不可能的状态”,这将使定义有意义的调查过程变得困难。 本报告提供了两份欺骗解密证明文件,它们可以验证但不要求正确的明文。
瑞士邮政尚未确认本文的分析,NSWEC声称此问题不会影响iVote系统。在非交互式零知识证明的实现中,还将列出其他问题的集合。这些引起了人们的关注,尽管目前尚不清楚如何利用它们。
0x01 Introduction
在瑞士邮政-Scytl sVote投票系统中,证明该系统收到的票数正确的过程有两个主要部分。首先是一系列证明,证明投票正确地进行了一系列混合服务器置换和重新分配的顺序,然后提供了由输入密文表示的投票集与输出中的匹配的证明。第二个是解密:必须对混合密文进行解密,并证明其包含当局要求的明文。在sVote中,每个混合器在随机播放后执行部分解密。
在早期的工作中证明了瑞士邮政-Scytl实施的随机播放证明包含一个陷门,允许混合器操纵选票但通过验证。在这项工作中为解密证明显示了类似的结果:Fiat-Shamir启发式算法实施中的错误使作弊机构能够产生适当解密的证明,通过验证,但声明了除纯明文之外的内容。
这使解密证明的合理性无效,实际上使sVote审计提供完整的可验证性的论点:由于验证程序是基于显示为错误的假设,因此无法成功完成就不能得出任何结论。有趣的是,观察到Verifiability Security Proof报告中描述的解密证明与sVote协议规范中出现的解密证明不同,后者是在受审查系统中实现的一种证明。
该安全证明报告中描述的证明似乎是正确的。为了证明缺少该解密证明的合理性可能造成的影响,展示了一种利用其中一个恶意授权(例如,系统的CCM1)在(部分)解密过程中修改所选选票并伪造解密证明的漏洞与有效值没有区别,因此可以通过验证。
这种特定的利用有两个局限性,但不排除利用其他和可能更危险的方式利用同一弱点的方法。
1.为了伪造解密证明并完成有效的改组证明,作弊CCM需要知道用于加密要修改的选票的随机性。这可以通过破坏有投票权的客户端或不良的随机数生成器来实现。
2.作弊机构在进行防混洗工作时,不能声明任意错误的明文。但是对于任何密文,它都可以证明它解密为明文之外的其他东西。 这一漏洞产生了一个可能是无用票而非有效投票的产出。然后,该漏洞利用可用于政治利益,以使作弊者不同意的那些选票无效。
A.是否可以检测到或归到作弊证明者?
由于这些无效的投票,这种利用可能会留下证据证明出了点问题。根据sVote审核规范,无效选票存储在auditableVotes.csv文件中,并且审核验证该文件中包含的所有选票确实无效。因此,已为其生成伪造的解密证明的选票将被写入该文件中,并且根据审核规范,验证将正式通过。
如果有人希望进一步调查,人们可能会想知道如何在选票箱中接受无效的选票并进行计票。投票规范指出:“通常不会发生这些错误,因为由投票客户端加密的值是选票中包含的有效质数的乘积。”目前尚不清楚“通常”是什么意思,或者如果发生这些错误,则可以推断出什么。
对于常规(即非写入)投票,似乎在提议的信任模型下不应发生这种情况。由投票客户提供的有效投票结构的零知识证明有望证明选票具有一定的内部一致性(即使它们不包括证明投票是产品的证据)应该是素数)。但是,还有另一个步骤,其中,投票验证上下文会得出选择返回码,如果投票不是预期素数的乘积,则该步骤通常将失败。
结果,漏洞利用似乎会使系统处于“不可能的状态”,这将使定义有意义的调查过程变得困难。如果考虑了破解密码算法的可能性(但可能并不真正知道哪种算法),那么最终可能可以通过要求CCM释放其密钥来识别作弊者。在不破坏某些选票的私密性的情况下,如何进行如此出色的调查无疑是未知的。
对于写入( write-in)票,单独的可验证性机制不能保证提交的写入有任何意义(这很复杂,因为它们本质上可以是任何东西)。因此,漏洞利用将提供一种将有效写入内容转换为无意义投票的方式,并且这种情况与愿意表达无意义写入内容的投票人或腐败的投票客户是一致的。
形式化地验证将通过。非形式化地显然存在问题。但是,如果在Fiat-Shamir变换中发现的弱点未知,则很难正确诊断此问题,特别是在不侵犯某些选票权的情况下。
B.实施
在此报告中提供了两个通过验证但更改了明文的解密证明示例,该方法在后面进行了说明们尚未实现将伪造的解密证明包含在sVotemixing和解密序列中。本文指出了在投票中实施的零知识证明中的其他几个问题,不知道这些是否会导致其他攻击。
0x02 Pitfalls of the Fiat-Shamir transform
Fiat-Shamir变换是一种将交互式证明转换为非交互式证明的标准方法。非形式化地讲,这个想法很简单:证明者无需等待验证者产生随机挑战,而是通过散列证明者的最初承诺来产生挑战。假设哈希函数的行为就像一个随机预言,这可以证明是安全的。
这样,该策略仅在非自适应设置中起作用,在该设置中,将证明状态提前提供给证明者和验证者。但是,当转移到证明者可以选择要针对其进行证明的陈述的自适应设置时,将陈述完全包含在哈希函数的输入中就变得至关重要,否则公正会崩溃。自适应安全性的要求在表决系统中非常普遍,正如在此处演示的那样,sVote协议也需要它。
问题在sVote系统中,协议规范或代码均未始终包含要在用于生成零知识证明中的挑战的哈希函数输入中待证明的完整语句。例如,正确解密密文(C0,C1)的证明不会散列C0。这允许作弊证明者计算有效的证明,然后根据该证明选择一个陈述,这破坏了证明的可靠性。
解决问题Fiat-Shamir变换的所有使用都应包括所有数据(包括要证明的语句),作为哈希的输入。特别是,正确解密的证明应包括C0(并且用于计算C0的基组生成器g也正确)。
这不仅适用于解密证明,而且适用于系统中存在的其他证明。
0x03 Producing a false decryption proof
请记住,具有公钥pk的消息m的ElGamal加密是一对(C0,C1)=(g^r,m(pk)^r)。知道秘密密钥x的任何人都可以构造正确解密的证明(密文(C0,C1)解密为消息m)。 pk = g^x mod p。它包含一个证明:
sVote的解密证明使用非交互式版本的Maurer’s Unified Proofs Prover 证明上面等式。该方法遵循众所周知的证明方法Chaum-Pedersen。
假设证明者(知道x)具有ElGamal密文(C0,C1),该密文由生成器g和公钥pk = g^x计算。她希望证明该密文可以解密为m,因此她计算C1 = C1/m并证明C’’1是该密文的正确解密因子,即C’’1 = Cx0或等效地等于( g,pk,C0,C1,m)满足方程式。她计算出Chaum-Pedersen证明如下:
证明是(c,z), 通过重新计算:
进行验证,然后验证c = H(pk,C‘’1,B0,B1)。
A.解决问题
问题在于,在第3步中,散列中不包含C0(g也不包含)。这允许自适应作弊证明者通过首先计算c,然后选择C0来生成伪造证明。
可以看出,(c,z)通过验证作为(g,pk,C0,C’’1)满足等式的解密证明。但是,这不太可能是真实的,即C’’1 = Cx0。以对数g为底,仅当s = x(t + sc)/z(mod q),即s(z-cx)= xt(mod q)或使用z的定义时,该方程式才能满足sa = xt(mod q)。但是a,s和t是从Zq中选择的独立值(其中q是ElGamal组的大小,建议参数为22047左右),因此这种巧合发生的可能性很小。因此,有一个不成立事实的有效证明。
注意到上述作弊策略并不依赖于a,s和t的随机性:可以为它们选择任何值,并且证明仍然被认为是有效的。尚不清楚具体选择是否会导致更危险的攻击。
还想强调指出,这个问题在Maurer的框架中不存在:该框架专注于交互式证明设置,因此不依赖于Fiat-Shamir变换。
B.转换为一组通过验证的伪造解密证明
解密证明[Scy18c,第9.1.8节]继续进行,说明了密文(C0,C1),声明了明文P1,然后对(g,pk,C0,C1 / P1)进行了Chaum-Pedersen证明。但是,没有什么可以迫使恶意证明者按此顺序进行操作。例如,可以从上面的作弊Chaum-Pedersen证明开始,并使用它来生成一组作弊解密证明文件:给定伪造证明(c,z)和相应的对(C0,C’’1),只需进行设置C1 = C’’1P并声明它是P的有效加密。无论是否正确,伪造的证据都将支持它。
C.将伪造的解密证明纳入sVote混合和解密序列
攻击者可以利用上述Chaum-Pedersen协议中的漏洞,原因是sVote具有非常特定的功能:每个混合器执行随机播放和该随机播放的输出的(部分)解密。这意味着混合器可以完全按照上述步骤进行:计算伪造的解密证明和匹配的密文(C0,C’’1),然后以这样的方式定义其混洗,以使带有正确C0的密文从中出来。
更准确地说,假设CCM1作为混合和部分解密的输入密文列表的一部分,包含密文(D0,D1)。它需要在其混洗中包括该密文,并输出其部分解密的版本,以及证明这些操作已正确执行的证据。但是,它希望修改该密文的内容,以使它变得无效并且不会在记帐中被考虑。它将通过声明一个虚假解密并使用上述作弊证据证明它是正确的来做到这一点。
首先,它会生成伪造的解密证明和匹配的密文(c,z,C0,C’’1)。现在,为了能够产生随机播放的证明(假设该证明是合理的),需要定义C1,以使对(C0,C1)实际上是(D0,D1)的重新加密。为此,它计算E0 = C0 / D0和E1 = Ex0。现在(E0,E1)是1的加密,因此(D0,D1)·(E0,E1)=(C0,D1E1)。因此,它可以简单地设置C1 = D1E1,这是对投票的真正重新加密。然后将P设置为C1 / C0 1可以使(c,z)成为(C0,C1)解密为P的有效证明,尽管(几乎可以肯定)这不是真的。
最后一个困难是使混洗工作证明有效。密文(C0,C1)是(D0,D1)的重新加密,因此混洗仍然有效。但是,证明要求知道在CCM1不知道的重新加密因子中使用的随机性,除非CCM1在基g中具有D0的离散对数。的确,如果D0 = g^r,则E0 = g^[(t + sc)/ z-r],完成随机证明所需的重新加密因子为(t + sc)/z-r.
这将要求信息从有投票权的客户端泄漏到服务器(CCM1)。当两者都是由同一公司实施并由同一机构管理时,这似乎不是一个过分的要求。当然,这种信息泄露应该允许选举操纵与完全可验证性的主张相矛盾。
D.关于作弊和产生有效选票的可能性
在此处描述的攻击中,假设攻击者还必须生成真正的随机证明,则攻击者将获得有效的随机明文。如果该随机明文对应于有效投票的编码,则攻击当然会更加隐蔽。在瑞士邮政系统中,这似乎极不可能,因为只有一小部分的明文是有效票,因此产生的票将是无效的。
在其他地方,它主要取决于对投票进行编码的方法。例如,在新南威尔士州,有效票数非常大,因为有效票数可能是340多个候选人的排列。由于log2(340!)> 2047,必须使用多个2048位ElGamal密文对进行某些投票编码。因此不知道随机选择的明文匹配有效投票的机会是否不可忽略。如果这样做,并且以与sVote相同的方式实施了NSW解密证明,则攻击可能会将有效票改为另一张无关的有效票。
E.小结
假设第一个混合器(CCM1)已被攻击,并且他可以获得一些选民用于加密的随机性。然后,该混合器可以针对这些投票者产生的密文产生有效的随机证明和伪造的解密证明,从而使他们的投票无效。如果这个混合器知道随机性,当然会专注于使他不喜欢的候选人的选票无效。
0x04 Other issues affecting proof soundness
A.其他证明中的Fiat-Shamir变换
整个sVote代码库都使用了Fiat-Shamir启发式算法,因此可能有很多其他示例都不可靠的证据。没有检查其中的大多数,并且缺乏健全性的影响可能相差很大:先前的报告和当前文档中描述的错误在两种情况下都破坏了证据的健全性,但它们导致不同的漏洞利用。尤其是,所有基于Maurer通用协议的非交互式变体的sVote证明(包括Schnorr证明,Exponentiation证明…)似乎都不具有自适应安全性,这些证明供投票客户和客户使用。 CCM可以利用这一弱点是合理的。
为了说明,展示了第二个带有Schnorr证明的简短示例。投票审计文件描述了Schnorr证明的构造,该证明是r的已知证明,使得C = g^r。通过计算B = g^a,然后c = H(C | B),然后z = a + cr来计算证明。通过验证g^z = BC^c和c = H(C | B)来进行验证。但是,证明本身不包含对g的引用(即使g绝对是语句的一部分,g也没有输入到哈希函数中)。
结果,对于组中任何给定的C和B,可以计算c = H(C | B)并选择一个随机z,然后确定g =(BC^c)^(1/z)。即使没有理由认为证明者确实知道该离散记录这(根据协议规范)也将成为有效的Schnorr知识,证明在基础g中C的离散记录。
目前尚不清楚仅此一项将如何导致对系统的攻击。 CreateVote算法使用Schnorr证明生成带有证明的证明。标准组生成器g,在这种情况下,证明者不会选择。该证明的健全性取决于外部因素还是令人不安的。
B.OR证明中缺少验证步骤
该代码库定义了一个n分之一的零知识证明构造(OR-Proof),其中包含一个严重缺陷,该缺陷将使恶意证明者可以诱骗验证者接受不属于所需n元素集的元素。
在定义良好的1-out-of-n协议中,验证者发送了一个挑战c(或由随机预言提供),证明者需要回答n个挑战c1,…cn,使得c为ci之和。然后,验证者必须验证这种相等性:如果不满足,则协议的健全性将完全中断,并且即使所有n个语句均为假,证明者也可以做出通过验证的证明。
在Swiss Post / Scytl代码库中,不执行此检查,其结果是可以使验证者被欺骗来验证没有对OR证明应该检查的任何元素进行编码的证明。
sVote协议未使用此ORProof,并且与Scytl确认,OR证明构造未在任何主动表决系统中使用,仅在内部原型中使用。即使有此警告,提交给全国选举的代码库中还存在另一个零知识协议结构,这使人们进一步怀疑该代码的完整性。
C.非抗冲突哈希函数
哈希函数以字符序列输入数字,而没有描述长度或类型。例如,这意味着31,7将散列为与317和3、17相同的事物。目前尚不清楚可以用来生成错误的证明,但是它打破了安全哈希函数背后的主要密码学假设-它的行为肯定不像随机预言。至少,这似乎使形式证明的假设无效。
在RandomOracleHash.java中,又有一个看似正确的实现。该哈希在混合网络中使用,但由于某种原因,在基于Maurer框架的证明库中使用了非抗冲突的哈希。
0x05 Conclution
在本报告中显示了sVote协议的完整选举可验证过程的第二个问题,这再次为Scytl-瑞士邮政系统中未被发现的选举欺诈开辟了道路。作弊的混合器可以伪造解密证明,并声称密文以某种形式通过了形式上的验证,从而将密文解密为真相之外的其他事物。
可验证的选举软件的目的是可验证的选举结果,而不是通过的证明。这项研究证实了任何公开民主的重要性,例如瑞士联邦条例所要求的。该系统的源代码必须公开,并且必须“可以从互联网上免费轻松获得。任何人都有权出于构想目的检查,修改,编译和执行源代码,并在其上撰写和发表研究报告。
由于这一过程,在与澳大利亚新南威尔士州(NSW)举行的大选有关的代码中也发现了至少一个本文公开描述的问题,该代码无法公开审查和讨论。显然,新南威尔士州使用的软件与Swiss Post/ Scytl系统有很大一部分代码相同。否则,这可能意味着无法察觉的选举作弊机会将在连续的选举中被忽略。