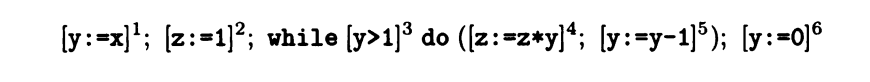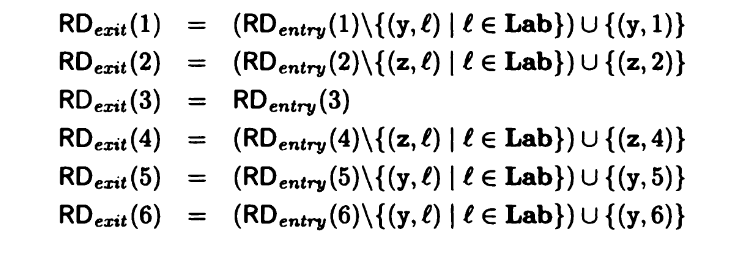前言
本文是程序分析理论系列的第二篇,内容为数据流分析的介绍及可计算的简单验证
数据流分析 Data Flow Analysis
定义方式及可计算性验证 Define mode and computability verification
在数据流分析法中,将程序转化成流程图是第一步。流程图包括代码块,和代码块之间的逻辑关系。
下图为一个示例。依旧以上一篇文章中的代码为例,转化为流程图则如 Figure 1所示
Figure 1
和上一篇文章中描述程序的方法类似,[ ]将表达式包裹,右上角为标签,除此之外多了表示逻辑关系的箭头以及简单的标记 如(yes or no)来确定分支。
接下来,为了让分析器能够获取信息,我们将流程图转化成一系列方程,来将代码逻辑关系用数学的方式表示出来。依旧延续着上一篇文章的定义原则。将一句代码划分为入口状态RD entry和出口状态RD exit 同时用形如 (v,l) 的表达式来定义关于v变量的改变。我们以第一句为例子做一个演示。原代码为 y = x 的一个赋值语句。RD exit(1) 就可以等价于 RD entry(1)中 y 的赋值语句 (y,l) 并上 此时y的赋值语句(y,1)。此时的 l 为在这一段代码开始之前的对于代码进行定义后的那个赋值语句的标签。而这个标签存储在 Lab 中。Lab是存储 l 的一个表格。完整的表示如图所示。
此时,我们将代码的本身数理结构表达清楚了,还要对语句之间的逻辑关系进行表达。即这一句代码的入口状态是哪一句代码的出口状态。我们可以简单的用形如RD entry (2) = RD exit(1)的方程进行定义。
上述的定义方法本身很容易想到正如同我们认为分析代码一样,变量的值从哪来到哪去,代码逻辑从这一句到那一句,但是,我们需要验证我们所提供的方程式具有可计算性。
关于可计算性的验证需要半序集和完全格的知识
预备知识 Preliminaries
半序集 partially ordered set
半序关系是一种具有反射性,传递性,反对称性的关系
半序集是具有半序关系的集合
取一个半序集 L 的子集 Y ,存在 l 属于 L ,假设 任取一个 l’ 属于 Y 满足 l’ 包含于 l 那么将 l 作为上限。同样的 假设 任取一个 l’ 属于 Y 满足 l 包含于 l‘ 则 l 为下限。当存在最大的下限和最小的上限时,就称他为有上确界和下确界。
完全格 complete lattice
格 是一种特殊的偏序集
完全格 是所有子集都有上确界和下确界的半序集
同时,完全格有一个定理 即 有上确界的半序集一定有下确界反之亦然。
对于两个半序集的映射关系具有以下性质:
1.满射 即 任意取L1中的一个元素对应的映射一定在L2中且一 一对应
2.如果 l包含于 l‘ 那么 f (l) 包含于 f (l’)
3.f (l ∏ l’) = f (l) ∏ f (l’) 并集一样
4.f (ㄩ Y) = ㄩ’{f (l’) | l’ ∈ Y } 下限一样
构造完全格 constructure of complete lattice
构造完全格有以下几种方法:两个完全格的笛卡尔积,一个集合和一个完全格在满射关系下构成的新集合,两个完全格在单调关系下构成的新集合。
笛卡尔乘积是集合的运算符,表示了两个集合构成新的集合的所有元素
论证:两个完全格的笛卡尔积依旧是一个完全格:
L1 = (L1,с1) L2 = (L2,с2) —> L = L1 X L2 = { ( l1 , l2 ) | l1 ∈ L1 ^ l2 ∈ L2}
因为 L1 和 L2 都是完全格,都有上确界和下确界,所以 l1 和 l2 都有最小的最大值和最大的最小值。也就是说,对于L 存在( l1, l2 )是L 的上确界和下确界。
论证:一个完全格和一个集合在满射的函数关系下构成的新集合是完全格:
我们定义L1 是完全格 ,S 是一个集合
L = {f : S -> L1 | f 是满射的}
每一个属于S 的s都对应一个属于L1 的l1,也就是说新集合L 依旧有着上确界和下确界
论证:两个完全格在单调函数关系下构成的新集合是完全格:
L1是完全格,L2 是完全格 ,f是单调函数关系
L = {f :L1 -> L2 | f 是单调的}
即L1 的上确界和下确界一一对应L2 的上确界和下确界,显然L也是完全格
链 chain
我们将集合各元素组成链用以研究集合内部关系
根据集合各元素不相同,且完全格具有上确界和下确界。我们可以构造一条上下界明确的单调链。以下界为极限则单调递减,以上界为极限则单调递增。
讨论
接下来,我们来讨论关于上文的方程可计算问题
我们把所有定义的RD exit 和RD entry 作为参数定义一个函数关系 即 将一系列代码执行流程与某个位置的代码入口状况进行映射。
而所有的RD构成一个半序集,也就是说这个函数关系是满足我们刚刚提到的两个半序集的映射的。也就是说每一种执行流程对应不同结果,如果某个执行过程包含于另一个执行过程,那么 那个执行结果一定也包含于另一个执行结果。
所以我们可以做出下面的判断 :如果 RD exit(2) 包含于 RD’ exit(2) 且 RD exit(5) 包含于 RD’ exit(5) 那么 RD exit(2)∪RD exit(5)包含于RD’ exit(2)∪RD’ exit(5) 也就是说这个函数是单调函数。我们可以列出这样的关系式 F (RD) 包含于 F’ (RD) 并且可以递进 。由于代码执行过程是有限可能的。所以存在某个n 使得F^(n+1) (RD) = F^n (RD)。当n取0时 即 RD = f (RD) 那么RD就是我们所找到的最小的解决方案。 他既包括了最终结果的可能值,也包括了一些不可能值,即 满足代码分析的近似解原则。所以关于上文的方程是可解的。
结语
内容不完善之处请见谅,欢迎各位指点,如有问题可联系我。