ChainFlag是一个区块链主题的CTF OJ平台,个人感觉现有题目质量很高,值得一做,这里分享下自己做题的过程。
EVMEnc
题目简介
题目提示简单的EVM加密,给了两个附件,info.txt与source.sol,附件如下图所示:
info.txt
transaction
1.
0x81200224..................
2.
0xffdd8131000000000000000000000000000000000000000000003100e35e552c1273c959
sload(0) = 208645382789328542577309
3.
0xffdd8131000000000000000000000000000000000000000000001ac3243c9e81ba850045
sload(0) = 29341064342757093333104
4.
0xffdd8131000000000000000000000000000000000000000000005ce6a91010e307946b87
sload(0) = 227103917449451505785192
5.
0xe6dc28ae..................
sload(3) = 1970527074032043059410457910532573615730510348629701619382
source.sol
pragma solidity ^0.5.10;
contract EVMEnc {
uint public result;
string public key;
uint private delta;
uint public output;
uint32 public sum;
uint224 private tmp_sum=0;
uint32 private key0;
uint224 private t0=0;
uint32 private key1;
uint224 private t1=0;
uint32 private key2;
uint224 private t2=0;
uint32 private key3;
uint224 private t3=0;
constructor() public {
delta = 0xb3c6ef3720;
}
function Convert(string memory source) public pure returns (uint result) {
bytes32 tmp;
assembly {
tmp := mload(add(source, 32))
}
result = uint(tmp) / 0x10000000000000000;
}
function set_key(string memory tmp) public {
key = tmp;
}
function cal_(uint x) public {
uint tmp = Convert(key) / 0x10000000000000000;
result = tmp % x;
}
function Encrypt(string memory flag) public {
uint tmp = Convert(flag);
uint key_tmp = Convert(key) / 0x10000000000000000;
assembly {
let first,second
sstore(5, and(shr(96, key_tmp), 0xffffffff))
sstore(6, and(shr(64, key_tmp), 0xffffffff))
sstore(7, and(shr(32, key_tmp), 0xffffffff))
sstore(8, and(key_tmp, 0xffffffff))
let step := 1
for { let i := 1 } lt(i, 4) { i := add(i, 1) } {
first := and(shr(mul(add(sub(24, mul(i, 8)), 4), 8), tmp), 0xffffffff)
second := and(shr(mul(sub(24, mul(i, 8)), 8), tmp), 0xffffffff)
sstore(4, 0)
for {let j := 0 } lt(j, 32) { j := add(j, 1) } {
sstore(4, and(add(and(sload(4), 0xffffffff), shr(5, sload(2))), 0xffffffff))
let tmp11 := and(add(and(mul(second, 16), 0xffffffff), and(sload(5), 0xffffffff)), 0xffffffff)
let tmp12 := and(add(second, and(sload(4),0xffffffff)), 0xffffffff)
let tmp13 := and(add(div(second, 32), and(sload(6),0xffffffff)), 0xffffffff)
first := and(add(first, xor(xor(tmp11, tmp12), tmp13)), 0xffffffff)
let tmp21 := and(add(and(mul(first, 16), 0xffffffff), and(sload(7),0xffffffff)), 0xffffffff)
let tmp22 := and(add(first, and(sload(4),0xffffffff)), 0xffffffff)
let tmp23 := and(add(div(first, 32), and(sload(8),0xffffffff)), 0xffffffff)
second := and(add(second, xor(xor(tmp21, tmp22), tmp23)), 0xffffffff)
}
sstore(3, add(sload(3), add(shl(sub(192, mul(step, 32)), first), shl(sub(192, mul(i, 64)), second))))
step := add(step, 2)
}
}
}
}
题目分析
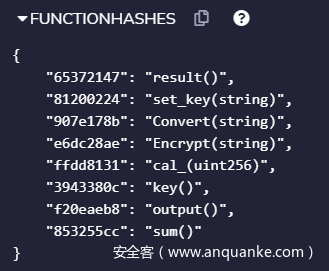
题目提供的两个附件source.sol为智能合约源码,info.txt为具体的交易序列,包含了交易的输入数据以及执行后部分存储storage的状态。利用remix编译智能合约,在Compilation Details中查看Functionhashes如下图所示:
分析info.txt文件,文件给出了5条交易的部分输入信息以及部分执行后的状态。以第一条为例:
1.
0x81200224..................
给出了交易发生的输入的前4个字节为0x81200224,交易输入的前4个字节一般对应了调用方法的哈希,后面的输入为调用方法使用的参数,这里调用了方法set_key(string),但是隐去了string参数的的具体内容。
分析第二条交易信息:
2.
0xffdd8131000000000000000000000000000000000000000000003100e35e552c1273c959
sload(0) = 208645382789328542577309
对应交易的方法为cal_(unit256),参数为0x3100e35e552c1273c959。sload(0)返回的是storage[0]的信息,根据合约对应的是全局变量result,意思是执行完交易后,result=208645382789328542577309
对info.txt中的信息继续处理,结果如下所示:
transaction
1.set_key(string memory tmp)
2.cal_(uint 0x3100e35e552c1273c959)
result = 0x2c2eb0597447608b329d
3.cal_(uint 0x1ac3243c9e81ba850045)
result = 0x6369510a41dbcbed870
4.cal_(uint 0x5ce6a91010e307946b87)
result = 0x301753fa0827117d1968
5.Encrypt(string memory flag)
output =0x505d433947f27742f60b06f350f2583450a1f7221380eeb6
到这里题目的基本要求和大题思路算是比较清楚了,题目算是一个利用solidity语言构造的一个加解密题目,题目设置未知的key值,然后告知调用三次cal_函数的结果,之后要求通过flag加密后的输出求出flag。
下面的重点在于分析cal和encrypt函数,这两个函数的编写加入了内联汇编,汇编指令的理解可以参考文档,总体而言都是对sotrage、memory以及stack的操作。本人作为一个菜狗子主要通过以下这样的方式来帮助理解,一是通过本地动态调试,题目给出了源码,可以利用remix本地部署并对相关函数进行调试,二是将用python重写函数,这样也方便了后续的解密程序编写。
通过调试可知cal函数可以理解为取余,已知:
0x2c2eb0597447608b329d = tmp % 0x3100e35e552c1273c959
0x6369510a41dbcbed870 = tmp % 0x1ac3243c9e81ba850045
0x301753fa0827117d1968 = tmp % 0x5ce6a91010e307946b87
求解取余方程可以利用中国剩余定理,具体实现附在最后。
求出了tmp后,分析Encrypt函数,先看循环前的部分:
uint tmp = Convert(flag);
uint key_tmp = Convert(key) / 0x10000000000000000;
assembly {
let first,second
sstore(5, and(shr(96, key_tmp), 0xffffffff))
sstore(6, and(shr(64, key_tmp), 0xffffffff))
sstore(7, and(shr(32, key_tmp), 0xffffffff))
sstore(8, and(key_tmp, 0xffffffff))
之前所求的tmp就是这里的key_tmp,那么存储在storage[5]到storage[8]都是固定值可以直接求出。后续部分用到的sload(2)是取storage[2]的值,按照源码分析对应的是变量delta=0xb3c6ef3720。storage[3]对应的output用来存储结果,由循环部分每次循环计算的结果移位拼接而成。将Encrypt函数重写成python,转化过程中需要注意符号的优先级,结果如下:
tmp = flag #Convert(flag) 48 hex
key_tmp =0x6b65795f746869735f69735f6b65795f
sstore5 = 0x6b65795f # 0x6b65795f 74686973 5f69735f 6b65795f >>96
sstore6 = 0x74686973
sstore7 = 0x5f69735f
sstore8 = 0x6b65795f
sstore2 = 0xb3c6ef3720
sstore3 = 0
step = 1
sstore4listall = []//mark
for i in range(1,4):
first = (tmp >> ((24 - i * 8)+4) * 8) & 0xffffffff
second = (tmp >> (24 - i * 8) * 8) & 0xffffffff
sstore4 = 0
sstore4list = []
for j in range(0, 32):
sstore4 = ((sstore4 & 0xffffffff) + (sstore2 >> 5)) & 0xffffffff
sstore4list.append(sstore4)//mark
tmp11 = (((second * 16) & 0xffffffff) + sstore5 ) & 0xffffffff
tmp12 = (second + sstore4) & 0xffffffff
tmp13 = ((second >> 5) + sstore6) & 0xffffffff
first = (first + (tmp11 ^ tmp12 ^ tmp13)) & 0xffffffff
tmp21 = (((first << 4) & 0xffffffff) + sstore7) & 0xffffffff
tmp22 = (first + sstore4) & 0xffffffff
tmp23 = ((first >> 5) + sstore8) & 0xffffffff
second = (second + (tmp21 ^ tmp22 ^ tmp23)) & 0xffffffff
sstore4listall.append(sstore4list)//mark
sstore3 = sstore3 + ((first << (192 - (step * 32))) + (second << (192 - (i * 64))))
step = step + 2
print(hex(sstore3))
#sstore3 = 0x505d433947f27742f60b06f350f2583450a1f7221380eeb6
由以上这段加密过程求解flag,下面分析加密算法。算法主体是两层循环,第一层循环了3次,tmp为24字节,第一次循环求出的first和second是tmp的高位的0-4字节以及5-8字节,后续循环每次取8字节前部分为first变量,后部分为second变量。通过第二层循环后将first与second再度拼接组合,循环三次后为最终的输出。
第二层循环32次,其中的sstore4为storage[4]的存储值,初始为0并且随着循环不断变化,但是在3*32次的循环中与输入的flag无关,这96个数值是固定的,这里我设立了一个数组sstore4list用来存储记录,方便后续的解密。第二层的循环中的tmp11,tmp12,tmp13三个变量仅与second有关,first依据这三个值变化,tmp21,tmp22,tmp23三个变量仅与first有关,second依据这三个值变化,循环32次后为最后得到后续拼接的first与second。
依据主要逻辑可以理解为以下形式:
tmp = [a,b,c]
output =[]
t = 0
for i in range(0,3):
first = tmp[i][:16]
second = tmp[i][17:]
for j in range(0, 32):
tmp1 = unknow_1(second,sstore4[t])
first = (first + tmp1)& 0xffffffff
tmp2 = unknow_2(first,sstore4[t])
second = (second + tmp2)& 0xffffffff
t = t+1
output.append([first,second])
现在逻辑就清晰多了,先分组后加密在组合,类似于常见流密码的加密方式,对以上加密过程解密的逻辑可以理解为以下形式:
tmp = []
output =[a,b,c]
t = 0
for i in range(0,3):
first = output[i][:16]
second = output[i][17:]
for j in range(0, 32):
tmp1 = unknow_1(second,sstore4[t])
first = (first - tmp1)& 0xffffffff
tmp2 = unknow_2(first,sstore4[t])
second = (second - tmp2)& 0xffffffff
t = t+1
tmp.append([first,second])
下面为了实现解密,我需要完成充实细节,比如计算出其中的用到96次的不同的sstore4,比如变量的移位拼接操作的具体实现等,实现解密即可求解出flag,实现代码附在后面。
完整解题过程
中国剩余定理求解key_tmp:
import gmpy2
def crt(b,m):
for i in range(len(m)):
for j in range(i+1,len(m)):
if gmpy2.gcd(m[i],m[j]) != 1:
print("error")
return -1
M = 1
for i in range(len(m)):
M *= m[i]
Mm = []
for i in range(len(m)):
Mm.append(M // m[i])
Mm_ = []
for i in range(len(m)):
_,a,_ = gmpy2.gcdext(Mm[i],m[i])
Mm_.append(int(a % m[i]))
y = 0
for i in range(len(m)):
y += (Mm[i] * Mm_[i] * b[i])
y = y % M
return y
b = [0x2c2eb0597447608b329d,0x6369510a41dbcbed870,0x301753fa0827117d1968]
m = [0x3100e35e552c1273c959,0x1ac3243c9e81ba850045,0x5ce6a91010e307946b87]
key = crt(b,m)
print (hex(key))
print (str(hex(key)[2:-1]).decode('hex'))
解密代码实现:
sstore3 = 0x505d433947f27742f60b06f350f2583450a1f7221380eeb6
key_tmp =0x6b65795f746869735f69735f6b65795f
sstore5 = 0x6b65795f
sstore6 = 0x74686973
sstore7 = 0x5f69735f
sstore8 = 0x6b65795f
sstore2 = 0xb3c6ef3720
tmp = 0
step = 1
sstore4listall = []
for i in range(1,4):
sstore4 = 0
sstore4list = []
for j in range(0, 32):
sstore4 = ((sstore4 & 0xffffffff) + (sstore2 >> 5)) & 0xffffffff
sstore4list.append(sstore4)
sstore4listall.append(sstore4list)
for i in range(1,4):
first = (sstore3 >> ((24 - i * 8)+4) * 8) & 0xffffffff
second = (sstore3 >> (24 - i * 8) * 8) & 0xffffffff
sstore4 = 0
for j in range(0, 32):
sstore4 = sstore4list[31 - j]
tmp21 = (((first << 4) & 0xffffffff) + sstore7) & 0xffffffff
tmp22 = (first + sstore4) & 0xffffffff
tmp23 = ((first >> 5 )+ sstore8) & 0xffffffff
second = (second - (tmp21 ^ tmp22 ^ tmp23)) & 0xffffffff
tmp11 = (((second << 4) & 0xffffffff) + sstore5) & 0xffffffff
tmp12 = (second + sstore4) & 0xffffffff
tmp13 = ((second >> 5) + sstore6) & 0xffffffff
first = (first - (tmp11 ^ tmp12 ^ tmp13)) & 0xffffffff
tmp = tmp + ((first << (192 - (step * 32))) + (second << (192 - (i * 64))))
step = step + 2
print(hex(tmp))
print (str(hex(tmp)[2:-1]).decode('hex'))