前言
RITA 是一个用于检测 C2 通信流量的开源项目,由 GO 语言编写
本文主要介绍其分析器的工作原理,并借助 Python 代码逐步还原该算法
为方便阅读,以下涉及到的变量均参照源码搬运而来,读者可跳转至该项目后自行作对比分析
分析器源码地址:https://github.com/activecm/rita/blob/master/pkg/beacon/analyzer.go
该算法对同源-目的IP间的通信,进行分数计算得到 score,其值分布为 0~1 之间,趋近 1 则疑似 beacon 通信行为
具体计算过程大致上可以分为两部分,根据通信间隔和数据包大小的特征,分别计算出 tsScore 和 dsScore,最后取均值得到 score
其中,tsScore 和 dsScore 的计算过程相似,下面开始针对各个部分做具体分析
tsScore的计算
tsScore 的计算又细分为三个部分:tsSkewScore、tsMadmScore、tsConnCountScore
tsSkewScore
该值的计算原理在源码中的注释部分也有所解释,即:理想的 beacon 通信行为应该具有通信间隔和数据大小呈现对称分布的特征
意思也很好理解,以 CobalStrike 默认的 beacon 配置为例,其通信行为如下图所示:
CS 默认回连的间隔时间为 60 秒,即使加上抖动(jitter),理论上仍然会呈现出高度对称的分布特征,其数据包大小亦如是
这里采用Bowley 偏度公式来度量对称性,得到偏度系数 tsSkew 和 dsSkew,后者在第二部分计算 dsScore 时会使用到
所谓的偏度系数,适用于描述曲线形状的对称性,其值在 1 到 -1 之间,分别代表着正偏斜或负偏斜,参照下图
具体计算时需要对数据集按大小顺序作四等分,在三个分位点依次取值:tsLow,tsMid,tsHigh
Python 示例代码:
# 根据时间戳计算通信间隔
http_df['deltas'] = http_df[timestamp].apply(lambda x: pd.Series(x).diff().dt.seconds.dropna().tolist())
# 以通信间隔为数据集,计算各分位点处数值
http_df['tsLow'] = http_df['deltas'].apply(lambda x: np.percentile(np.array(x), 25))
http_df['tsMid'] = http_df['deltas'].apply(lambda x: np.percentile(np.array(x), 50))
http_df['tsHigh'] = http_df['deltas'].apply(lambda x: np.percentile(np.array(x), 75))
# 根据公式:Bowley Skewness = (Q1 + Q3 – 2Q2) / (Q3 – Q1),计算分母和分子
http_df['tsBowleyNum'] = http_df['tsLow'] + http_df['tsHigh'] - 2*http_df['tsMid']
http_df['tsBowleyDen'] = http_df['tsHigh'] - http_df['tsLow']
# 如果分母为 0,Q2 = Q1 或 Q2 = Q3,则计算结果不可靠,tsSkew 取 0
http_df['tsSkew'] = http_df[['tsLow','tsMid','tsHigh','tsBowleyNum','tsBowleyDen']].apply(
lambda x: x['tsBowleyNum'] / x['tsBowleyDen'] if x['tsBowleyDen'] != 0 and x['tsMid'] != x['tsLow'] and x['tsMid'] != x['tsHigh'] else 0.0, axis=1
)
最后根据 tsSkew 算出:tsSkewScore = 1 – abs(tsSkew)
tsMADMScore
这一段计算的前提为:理想的 beacon 通信行为在其通信间隔的中位数周围应该具有很低的分散度
该特征可以用 MADM(Median Absolute Deviation about the Median)来度量
具体计算过程也比较简单,在 Python 中我们用一行代码就能搞定
http_df['tsMadm'] = http_df['deltas'].apply(lambda x: np.median(np.absolute(np.array(x) - np.median(np.array(x)))))
得到 tsMadm 和 dsMadm 后,设定 30秒 和 32字节 作为阈值,超出则分数计为 0
因为这里的分散度越低越好,由此可以计算出 tsMadmScore 和 dsMadmScore,以下是 Python 示例代码:
http_df['tsMadmScore'] = 1.0 - http_df['tsMadm'] / 30.0
http_df['tsMadmScore'] = http_df['tsMadmScore'].apply(lambda x: 0 if x < 0 else x)
http_df['dsMadmScore'] = 1.0 - http_df['tsMadm'] / 32.0
http_df['dsMadmScore'] = http_df['dsMadmScore'].apply(lambda x: 0 if x < 0 else x)
tsConnCountScore
跟上面的 SkewScore 和 MadmScore 不同,这一部分在 tsScore 和 dsScore 中的计算有所区别
在行为特征上,beacon 通信时往往具有较高的连接数,tsConnCountScore 正是用来度量这一点的
利用通信的持续时间和连接次数计算得到:tsConnCountScore = ConnectionCount / (tsConnDiv / 10.0)
其中,ConnectionCount 代表通信次数,tsConnDiv 由通信起止时间除以固定的连接频率得来,此处该值取为 10 秒
最后得分如果大于1,则向下舍入取1,因为连接得越频繁,越有可能是 beacon 通信
PS:对于这里的 10 秒,应该还存在优化空间,有研究员指出该值太小可能会影响最终得分从而产生漏报,传送地址
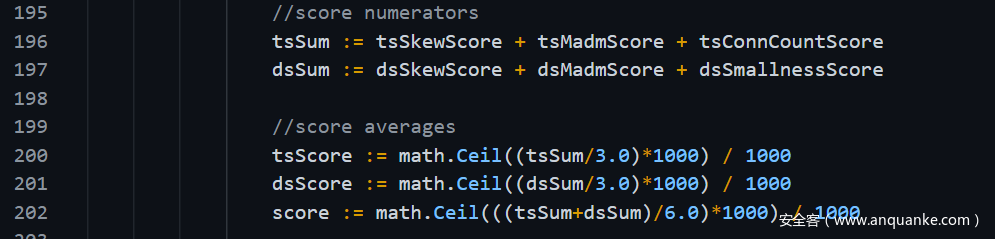
综上,计算 tsScore = (tsSkewScore + tsMADMScore + tsConnCountScore) / 3.0
dsScore的计算
数据大小的分散度(dsSkewScore)和 MADM(dsMADMScore) 的算法不变,前文已经有所解释
主要区别在于,计算 dsMADMScore 时数据大小的 MADM 以 32 字节作为阈值,数据包超出该大小则得分为 0
另外,由于 beacon 通常都是较小的数据包,这里采用 dsSmallnessScore 作为衡量指标
其含义为,如果数据包大小的众数(Mode)超过 65 Kb,则得分为 0
Python 示例代码如下:
# 计算数据包大小差值
http_df['size_deltas'] = http_df[data_size].apply(lambda x: pd.Series(x).diff().dropna().tolist())
# 计算 dsSkew
http_df['dsLow'] = http_df['size_deltas'].apply(lambda x: np.percentile(np.array(x), 25))
http_df['dsMid'] = http_df['size_deltas'].apply(lambda x: np.percentile(np.array(x), 50))
http_df['dsHigh'] = http_df['size_deltas'].apply(lambda x: np.percentile(np.array(x), 75))
http_df['dsBowleyNum'] = http_df['dsLow'] + http_df['dsHigh'] - 2*http_df['dsMid']
http_df['dsBowleyDen'] = http_df['dsHigh'] - http_df['dsLow']
http_df['dsSkew'] = http_df[['dsLow','dsMid','dsHigh','dsBowleyNum','dsBowleyDen']].apply(
lambda x: x['dsBowleyNum'] / x['dsBowleyDen'] if x['dsBowleyDen'] != 0 and x['dsMid'] != x['dsLow'] and x['dsMid'] != x['dsHigh'] else 0.0, axis=1
)
# 计算 dsSkewScore
http_df['dsSkewScore'] = 1.0 - abs(http_df['dsSkew'])
# 计算 dsMadmScore
http_df['dsMadm'] = http_df['size_deltas'].apply(lambda x: np.median(np.absolute(np.array(x) - np.median(np.array(x)))))
http_df['dsMadmScore'] = 1.0 - http_df['dsMadm'] / 32.0
http_df['dsMadmScore'] = http_df['dsMadmScore'].apply(lambda x: 0 if x < 0 else x)
# 计算 dsSmallnessScore
http_df['dsSmallnessScore'] = http_df[data_size].apply(lambda x: 1- (np.argmax(np.bincount(x)) / 65535))
http_df['dsSmallnessScore'] = http_df['dsSmallnessScore'].apply(lambda x: 0 if x < 0 else x)
最后得到,dsScore = (dsSkewScore + dsMADMScore + dsSmallnessScore) / 3.0
小结
最终得分:score = (tsScore + tsScore) / 2.0,完整的演示代码放在 这里
为了简单演示下狩猎效果,我用 Covenant 作为 C2 框架,生成 3 组数据,通信间隔在 10-60 秒不等,抖动在 10%-20% 之间
最后得分如下:
当然,这里只是为了验证该算法基本逻辑的正确性,数据样本太小,并不能说明其实际使用效果,切勿直接用作检测告警
它的目的是帮助我们提高威胁狩猎的效率,搭配其它工具和方法一起使用才是正确的姿势
例如可以将其输出作为我们检测规则的输入,或者结合威胁情报食用,进行二次确认
另外,不要忘了对输入数据做好预处理和清洗工作,比如聚焦特定协议,判断内外网IP,过滤白名单主机等等,这会大幅提高分析效率和检测效果
当然,算法本身还有很大的优化空间,尤其对计算过程中涉及到的一些常量,我也有不少的疑问
例如,Mehmet Ergene 在其文章中提到过可能会产生的漏报:
- 通信间隔的 MADM 大于 30 秒时,则 tsMADMScore 分数为 0
- 数据大小的 MADM 超过 32 字节时,则 dsMADMScore分数为 0
如果一个 beacon 的通信间隔为 10 分钟,抖动(jitter)为 20%,其 MADM 会超过 30s
这种情况下算出的 tsMadmScore 为 0,进而会降低总得分,导致漏报
最后,感谢 Mehmet Ergene 的分享,这篇文章受其启发而来,如有纰漏之处,欢迎私信交流