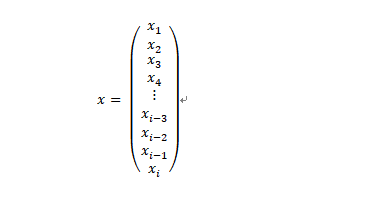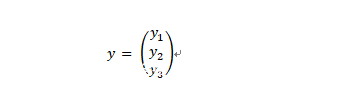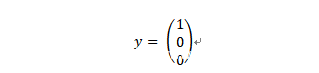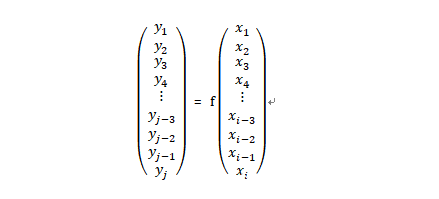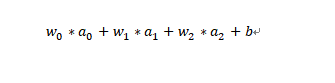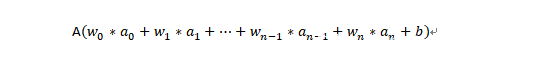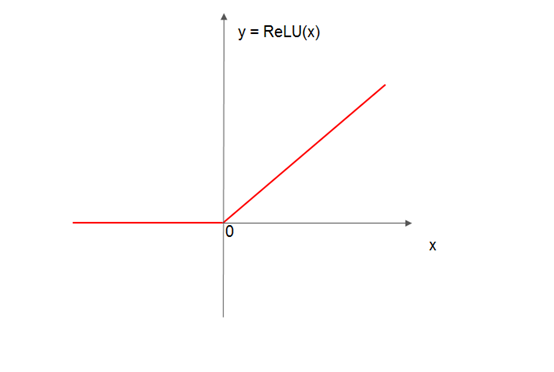在上一篇文章中,我们为读者介绍一些基本的概念,如什么是机器学习,什么是深度神经网络等。读者可能已经发现了,上文中,我们的主要使用示意图来介绍这些概念,虽然这种方式比较形象,但是,我们最终是要将这些概念转换成代码的——如果直接从示意图跨越到代码的话,感觉有些唐突,所以,这里需要一个过渡。
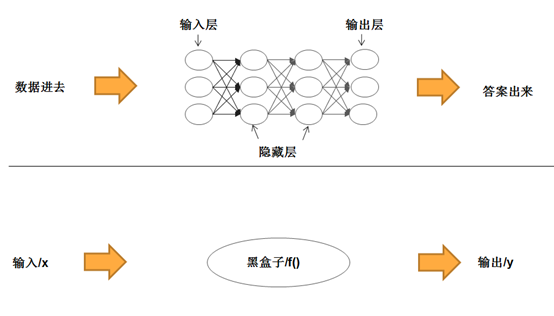
为此,我们将换个角度,用更为形式化的数学语言来描述这些概念,以便帮大家平滑地过渡到下一篇的内容:深度神经网络的代码实现。首先,我们可以把神经网络模型看作一个黑盒子,即函数。
把深度神经网络模型看作函数
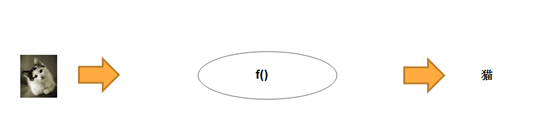
为简单起见,我们可以把深度神经网络看成是一个具有魔力的黑盒子,我们把一张照片塞进去,它就能告诉我们照片里面是否是一只猫:
图1 将神经网络看作一个黑盒子
当然,我们从黑盒子外边看的话,貌似它施展了某种魔法。但是,如果我们深入黑盒子里边的话,就会发现,它是对塞进去的照片进行了某种处理,或者说,进行了某种映射……等一下,好像有点耳熟,“映射”不是函数干的活么?是的,我们完全可以把黑盒子看成一个函数!因此,如果用数学语言来描述的话,我们的深度神经网络就可以表示为一个非常简洁的函数表达式:
y = f(x)
严格来讲,上面描述的是模型的使用过程,也就是推理过程,前提是我们已经求出了相应的函数f()。那么,我们自然会问,该如何求解这个函数呢?这就需要借助于模型的训练过程了,也就是前面说的,用训练数据确定特定架构的神经网络的相应参数的过程。
这时,您可能要问了,函数真有这么大的魔力吗?这个不用太担心,不是曾经有过这么一个段子吗:给数学家3个参数,他们就能用函数拟合出一头大象;如果给他们4个参数,他们就能让这头大象奔跑如飞。更何况,我们的模型的参数,可远不止三四个参数!
相反,现实中我们更应该担心的是函数的过拟合现象。比如,我们训练神经网络的人脸照片中,有些带有“青春痘”,结果模型注意到了这现象,并把它当成了人脸的一个特征,那么,很可能导致一旦照片中出现了类似“青春痘”的图形,就会被模型误认为是人脸照片!
把输入和输出看作向量
当我们将小猫的照片传递给神经网络的时候,实际上,接收该照片的是神经网络的输入层。我们知道,输入层是由许多神经元,或者说是节点或子函数组成的,那么问题来了?每个神经元收到的是一幅完整的照片呢,还是照片的一部分呢?
实际上,每个神经元收到的只是照片的一部分,准确来说通常仅仅是一个像素。假设我们的照片含有i(如28×28)个像素,并且照片是黑白色的,那么,每个像素都有一个明确的位置和灰度值(一个从0到255的整数值)。接下来,我们按照某种顺序组织照片的像素——比如,按照从上到下每次取一行;对于每行,按照从左到右的顺序每次取一个灰度值,将其排成一列:
大家可能已经看出来了,这就是一个列向量。就黑白照片来说,该向量的元素的取值范围为0到255。需要注意的是,如果输入层的每个神经元只接受一个像素的话,那么,就本例来说,输入层就需要28 x 28 = 784个神经元。很明显,上面示意图中的输入层中画出的神经元明显不够用,并且还需添加不少!但是,这只是一个示意图而已,大家明白意思就行了。
上面看到,我们的神经网络的输入可以表示为一个列向量,那么,输出能否也表示成一个列向量呢?答案是肯定的。举例来说:假设我们的神经网络能识别3种动物,比如,猫、虎和豹,那么,我们可以设计这样一个列向量:
其中,向量y的各个元素可能的取值为0和1,并且,最多只有一个元素的值为1。这样的话,我们就可以让y1=1照片中的动物为猫,即:
同时,让y2和y3的值为1时分别表示照片中的动物虎和豹。当然,只要您喜欢的话,也可以设计其他的对应关系。因此,假设我们的深度神经网络可识别的类别数量为j,那么,我们就可以用下列表达式来描述该网络了:
其中,i是我们的神经神经网络的输入层中神经元的数量,就本例来说,就是输入的照片中的像素的数量,即784个。同时,j是网络输出层中神经元的数量,在本例中为3个。
此前,我们一直将表示深度神经网络的函数作为一个黑盒子来看待,接下来,我们要深入了解一下它的内部运行机制。
黑盒子是如何给出答案的
前面说过,深度神经网络的输入和输出可以用向量加以表示,类似的,神经网络的各层也可以表示为向量。那么,这里向量的元素表示什么呢?前面说过,神经网络中的各个节点,无论你叫它神经元还是函数,本质都是一样的:接收输入,进行加工,然后给出输出值。所以,这里向量元素可用于表示函数和函数的输出,但本质上是一样的,因为每个函数都对应于一个输出,因此,不妨直接让该向量元素表示函数的输出吧!
实际上,当我们使用深度神经网络计算答案的过程,就是数据从前往后流经神经网络各层,并进行相应的加工的过程。接下来,我们就看看神经网络中的各层到底对数据做了些什么?
首先,对于输入层,可以简单认为,该层中的函数只是接收一个像素值,然后,原封不动地输出。这样,输入层的输出就可以形成一个向量了。接着,该向量中各个元素值将通过相应的连接传递给下一层,即第一个隐藏层。需要说明的是,每层中的各个函数,通常称为激活函数,其输出值,相应称为激活值,通常用字母a表示。
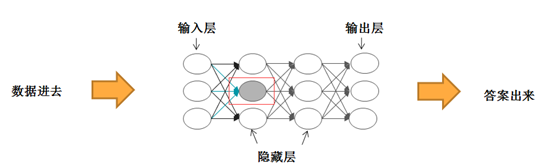
现在,数据流到了第一个隐藏层。那么,我们可能会问:第一个隐藏层中的每个函数的输入,是向量中的某个值(即标量),还是整个向量呢?答案是后者。我们还有一个疑问:数据流经层与层之间的连接时,是否发生了变化呢?答案是肯定的,每个连接都对应于一个权重值w,所有流经它的数据都会进行加权处理,比如对于下图中第一个隐藏层中间位置的激活函数来说,
图2 第一个隐藏层中的示例激活函数
为了得到其输入值,需要用到下列各项内容:
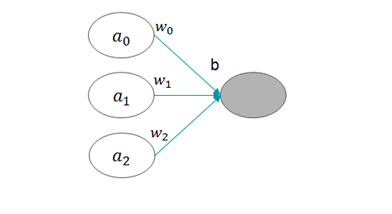
图3 激活函数的输入
上图中,a表示输入层的激活值,w表示相应连接上的权重值,其下标表示它们在向量中的位置。此外,我们还看到灰色神经元左边还有一个字母b,它表示什么呢?这是一个常数,通常称为偏置项。它实际上就是每个神经元所特有的一个偏差值,该值越大,该神经元越容易被激活。
到现在为止,终于将神经元的输入的构成要素介绍完了,下面给出输入的合成方法:
更一般地说,如果上一层中共有n个神经元的话,那么,后面这一层中每个激活函数的输入的计算方法为:
也就是说,当前神经元的输入就是上一层的激活值加权求和,然后加上当前神经元的偏置项。假设当前神经元采用的激活函数为A,那么,其激活值的计算公式为:
上面介绍了如何合成激活函数的输入,接下来,我们聊一聊激活函数本身。
对于神经网络来说,可供选用的激活函数有很多,例如softmax函数、tanh函数、ReLU函数,等等。但是,具体选用哪种类型的激活函数,要视神经网络的类型以及所在的网络层而定。例如,目前的深度神经网络的隐藏层通常采用ReLU函数作为其激活函数。该函数有一个特点,那就是输入小于一定阈值时,其输出一直为0;当输入值大于该阈值时,其输出值就是其输入。如果将阈值指定为0的话,则该函数的公式如下所示:
ReLU(x) = max(0, x)
下面给出该函数的示意图:
图4 ReLU函数
该函数的行为与动物神经元有一个相似之处,那就是刺激信号低于阈值时,神经元一律没有反应;只有刺激信号大于阀值后,神经元才被激活。这一特性非常有用,尤其是在训练深度神经网络过程中,因为它对于让炼丹师们闻风丧胆两个问题——梯度消失和梯度爆炸,还是有不错的效果的!
好了,上面介绍了第一个隐藏层中单个神经元如何计算其输入值,以及可以选用哪些函数来处理这个输入值,从而得到该神经元的输出值,或者说,该激活函数的激活值。实际上,该层中的所有神经元都会进行同样的处理,因此,该层就会得到一个由激活值组成的向量。该向量继续向下传递,并由第二个隐藏层进行类似的处理;然后,重复这个前向传播过程,直到输出层,我们就会得到相应的答案了。
小结
在本文中,我们为读者介绍如何从数学的角度来描述神经网络的输入和输出,以及对于一个训练好的神经网络,它是如何分辨照片中的动物是否为一只猫的——推理过程。但是,大家可能注意到了,这里的前提是已经有一个训练好的神经网络了,那么,这个神经网络是如何训练的呢?请大家不要着急,我们将在下一篇文章中跟大家一起探索这个问题。