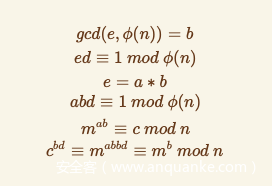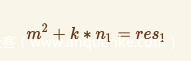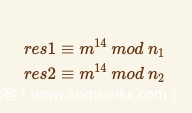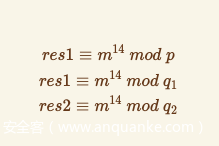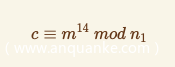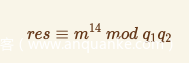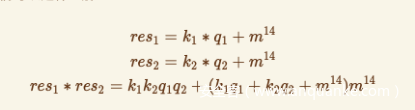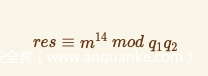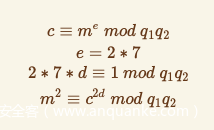前言
实在不知道起什么标题,于是滑稽了一波。写这篇文章的起源是2018高校网络信息安全管理运维挑战赛的一道RSA题目,借此机会,将中国剩余定理与RSA的结合研究一下。
题目描述
拿到题目很简短
身陷囹圄
发现
assert gcd(e1,(p1-1)*(q1-1))==14 assert gcd(e2,(p2-1)*(q2-1))==14
那么本能想到公约数的问题,于是尝试
gcd(n1,n2)
发现有公约数
12120327527644543811107783655014863098833219936714394976342507913322405566177432644931575840816861543106701611662013978324877080018872656490603706071067111
那么可以分解出p和q1,q2
p = gcd(n1,n2) q1 = n1/p q2 = n2/p
得到结果
p=12120327527644543811107783655014863098833219936714394976342507913322405566177432644931575840816861543106701611662013978324877080018872656490603706071067111 q1=12037827528067911684278967221392433256129944002157200272548317200308481572950474775891360447285969682243206009995242277136633522897723532096467191105943909 q2=12301580698247665838432962460247894405698817646605188562297985838079356879336309758823376086396761749681729993573203954506346863479448531269351981555913253
到目前为止一直很开心,因为成功的分解了p和q
那么是不是直接求逆元,得到私钥,就结束了呢?
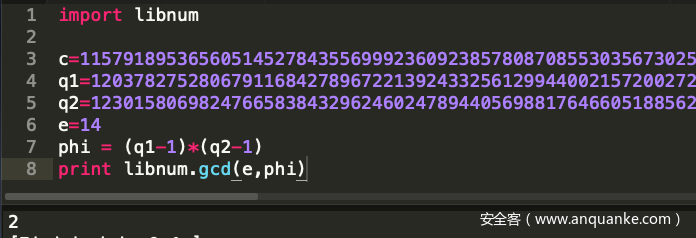
我开心的运行
print gmpy2.invert(e,phi)
直到报错,我才想起来
gcd(e,phi)=14
所以直接求逆元肯定是不行的
第一时间想到的是Rabin Attack,但是那是e=2的时候,所以此时陷入困境
公式代换
后来想到等式代换
我们知道b=14,此时a和phi(n)互素
那么可以求a和phi的逆元得到bd
gmpy2.invert(a,phi)
于是可以
pow(c,bd,n)
得到m^14 mod n1的值,于是同理:
n1得到一组m^14 mod n1的值
n2得到一组m^14 mod n2的值
可以得到以下方程组:
如果这里不是m^14,是m^2或者m^3
那么完全可以尝试爆破得到m
因为m^2不会太大,所以
那么完全可以使用低指数的思想去破解
然而这里是m^14,并不是啥低指数了。
中国剩余定理
虽然题目走的绝,但是他给了2组等式,那么这样的等式,仅仅为了让我们利用公约数分解p,q这么简单吗?答案显然是否定的
这里我们可以尝试中国剩余定理
二者联立,可以求出m的特值,但是这里的m值并不是真的flag的明文
因为m^14足够大,这里仅仅是个模数,可以理解为
flag=m+k*n1
依旧需要爆破k,如果flag的长度比较短,例如
flag={this_is_flag}
那么很快可以爆破出来,但是事实上,题目的格式都是
EIS{MD5(…..)}
估计一时半会儿出不来了
灵感乍现
在非常难受的情况下,学长给了我一些点播,我们刚才的做法,完全是对中国剩余定理使用的浪费,我们可以根据中国剩余定理得到如下3个式子
即模数分解,这样依旧可以计算出特解m
1157918953656051452784355699923609238578087085530356730257378716186056416448726997740518977363905297393271755641099448971883212306481009956454341821281132105675527179275608942496622728690548474209986204730278844220750782548612807173412632486533313585094360198798935868257031751209954691446183447044165077233401610378901936945171131038402147803394967428713339276583596523854139656861116867477243532939513114104962464919267716378905965731491698192883615068033313579
之前我们到这里为止,开始了爆破,无果而终。
那之前为什么我们不把现在这个局面当做
这样一个问题去解决呢?
这里的c我们已经求得,n1也是已知的,并且可以被分解,公钥e=14
因为这样无济于事,e依旧和phi(n1)有公约数。
那有没有办法换个模数呢,让phi与e互素
这里就是这道题的有趣之处:
我们可以将后2个式子合并
(注:为什么可以合并呢?)
我们可以这样理解
两边同时模q1q2,即可得到合并后结果
所以我们现在有等式
我们可以把他当做一个新的RSA题目:
密文等于中国剩余定理求出的m特解 公钥等于14 模数已经分解为q1和q2
水到渠成
那么这样一看,就是一个非常简单的RSA题目了
c=1157918953656051452784355699923609238578087085530356730257378716186056416448726997740518977363905297393271755641099448971883212306481009956454341821281132105675527179275608942496622728690548474209986204730278844220750782548612807173412632486533313585094360198798935868257031751209954691446183447044165077233401610378901936945171131038402147803394967428713339276583596523854139656861116867477243532939513114104962464919267716378905965731491698192883615068033313579 q1=12037827528067911684278967221392433256129944002157200272548317200308481572950474775891360447285969682243206009995242277136633522897723532096467191105943909 q2=12301580698247665838432962460247894405698817646605188562297985838079356879336309758823376086396761749681729993573203954506346863479448531269351981555913253 e=14
当我们兴致勃勃去求逆元私钥d时,又发现
这里的e和phi又不是互素的,有公约数2,乍一看非常头疼
实际上,这里的公约数2和14比实在太小了,所以我们可以直接破解:
按照之前的思路
2d可以通过7的逆元求得,由于2次方太小,所以直接对m开方即可
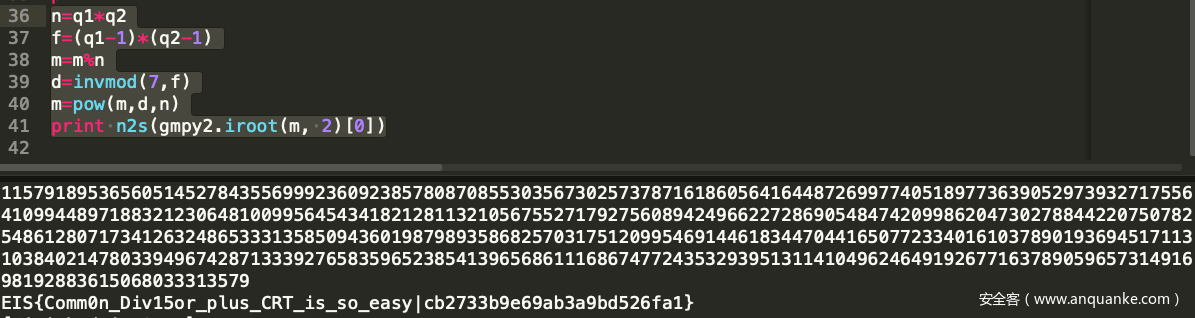
完整脚本如下
n1=0xcfc59d54b4b2e9ab1b5d90920ae88f430d39fee60d18dddbc623d15aae645e4e50db1c07a02d472b2eebb075a547618e1154a15b1657fbf66ed7e714d23ac70bdfba4c809bbb1e27687163cb09258a07ab2533568192e29a3b8e31a5de886050b28b3ed58e81952487714dd7ae012708db30eaf007620cdeb34f150836a4b723L e1=0xfae3aL c1=0x81523a330fb15125b6184e4461dadac7601340960840c5213b67a788c84aecfcdc3caf0bf3e27e4c95bb3c154db7055376981972b1565c22c100c47f3fa1dd2994e56090067b4e66f1c3905f9f780145cdf8d0fea88a45bae5113da37c8879c9cdb8ee9a55892bac3bae11fbbabcba0626163d0e2e12c04d99f4eeba5071cbeaL n2=0xd45304b186dc82e40bd387afc831c32a4c7ba514a64ae051b62f483f27951065a6a04a030d285bdc1cb457b24c2f8701f574094d46d8de37b5a6d55356d1d368b89e16fa71b6603bd037c7f329a3096ce903937bb0c4f112a678c88fd5d84016f745b8281aea8fd5bcc28b68c293e4ef4a62a62e478a8b6cd46f3da73fa34c63L e2=0x1f9eaeL c2=0x4d7ceaadf5e662ab2e0149a8d18a4777b4cd4a7712ab825cf913206c325e6abb88954ebc37b2bda19aed16c5938ac43f43966e96a86913129e38c853ecd4ebc89e806f823ffb802e3ddef0ac6c5ba078d3983393a91cd7a1b59660d47d2045c03ff529c341f3ed994235a68c57f8195f75d61fc8cac37e936d9a6b75c4bd2347L from libnum import * import gmpy2 p=gcd(n1,n2) q1=n1/p q2=n2/p assert(p*q1==n1) assert(p*q2==n2) f1=(p-1)*(q1-1) f2=(p-1)*(q2-1) tmp=gcd(e1,e2) e1=e1/tmp e2=e2/tmp d1=invmod(e1,f1) d2=invmod(e2,f2) m1=pow(c1,d1,n1) m2=pow(c2,d2,n2) m3=m1%p m2=m2%q2 m1=m1%q1 m=solve_crt([m1,m2,m3], [q1,q2,p]) print m n=q1*q2 f=(q1-1)*(q2-1) m=m%n d=invmod(7,f) m=pow(m,d,n) print n2s(gmpy2.iroot(m, 2)[0])
后记
当我们的公钥与phi不互素时,不仅有Rabin Attack解法了,这道题对中国剩余定理的灵活运用非常有趣XD