前言
Capture the Ether是一款在破解智能合约的过程中学习其安全性的游戏,跟ethernaut也类似,这是它的地址。
个人感觉质量非常高,比其ethernaut更加贴近实战,因为题目比较多,下面主要先放出Math部分的write up,这部分分值最高同时质量也相对较高,希望大家玩得愉快,其它部分等做完一起发吧
Warmup
这一部分是上手的教程,玩过ethernaut的同学应该就很熟悉了,也是在Ropsten测试网上的练习,在这我也就不多讲了
0x1. Deploy a contract
第一步是了解怎么操作部署合约,关卡里也写得很清楚了,首先按照metamask,可以直接在chrome的扩展商店搜索安装,然后切换到Ropsten测试链,当然首先是创建钱包设置密码,然后点击Buy按钮去水龙头取一些ether回来
接下来点击页面右边的红色的deploy即可然后在弹出的交易确认里点击submit即可成功将页面所示的合约部署到测试链上,接下来再点击check并确认交易即可
0x2. Call me
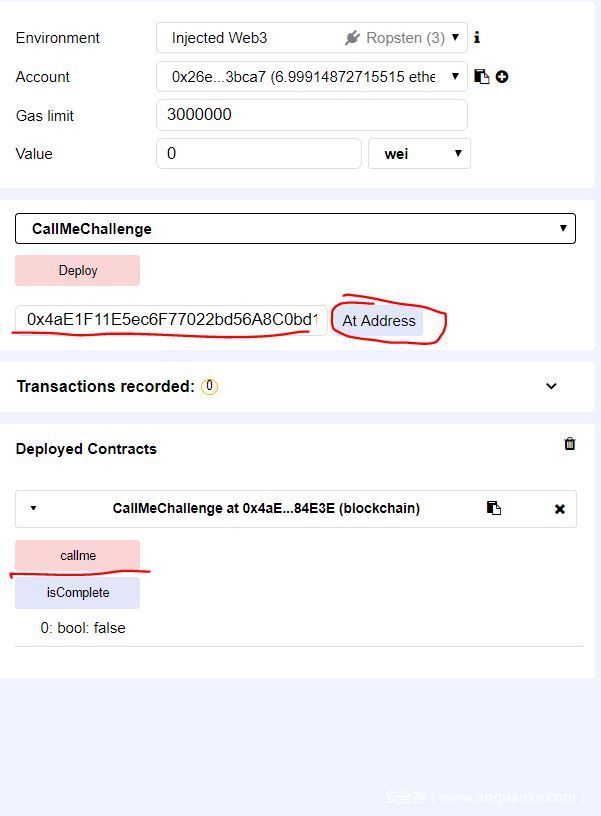
这个挑战的目的是让你调用一下部署的合约里的callme函数,方法其实很多,比较简单的我们可以直接在remix里进行调用,将合约代码复制过去后,先编译一下,然后在Run里面将环境切换为injected web3,然后在下面的deploy处将我们挑战的页面里给出的合约地址填上,点击at address即可
接下来在下方即可直接调用callme函数
调用之后点击isComplete就会发现已经变为true,然后即可返回挑战进行check
0x3. Choose a nickname
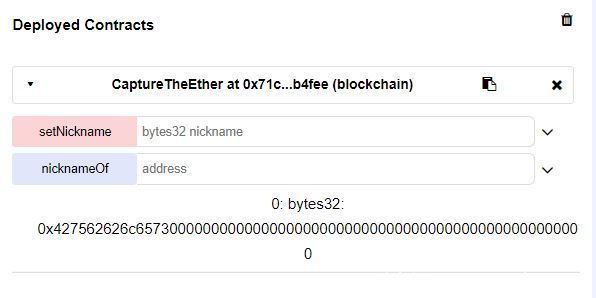
这一关是让我们设置自己的昵称,也就是在排行榜上显示的名字,其实也是调用个函数的事,操作跟上面一样,合约选择CaptureTheEther,地址填上,调用setNickname函数即可,注意参数填上自己昵称的16进制格式,然后用nicknameOf函数就能看到结果了
接下来返回挑战点击begin game按钮就会部署一个合约来检查你是否设置了昵称,check以后就能正式开始我们的闯关之旅了
Math
这部分挑战是有关solidity中的数学运算
0x1. Token sale
pragma solidity ^0.4.21;
contract TokenSaleChallenge {
mapping(address => uint256) public balanceOf;
uint256 constant PRICE_PER_TOKEN = 1 ether;
function TokenSaleChallenge(address _player) public payable {
require(msg.value == 1 ether);
}
function isComplete() public view returns (bool) {
return address(this).balance < 1 ether;
}
function buy(uint256 numTokens) public payable {
require(msg.value == numTokens * PRICE_PER_TOKEN);
balanceOf[msg.sender] += numTokens;
}
function sell(uint256 numTokens) public {
require(balanceOf[msg.sender] >= numTokens);
balanceOf[msg.sender] -= numTokens;
msg.sender.transfer(numTokens * PRICE_PER_TOKEN);
}
}
这个挑战合约实现了一个基本的买卖过程,通过buy我们可以买入token,通过sell我们可以消耗token,而目标是使合约拥有的balance小于1 ether,因为我们部署合约时已经为合约存入了1 ether,所以目标就是如何动员这不属于我们的ether
既然是在math类型下,肯定要在合约的算术运算上找漏洞,这里很明显在buy函数内就存在上溢,关键就在于此处的判断
require(msg.value == numTokens * PRICE_PER_TOKEN);
此处的msg.value是以ether为单位,因为一个PRICE_PRE_TOKEN就是1 ether,这里我们需要明白在以太坊里最小的单位是wei,所以此处的1 ether事实上也就是10^18 wei,即其值的大小为10^18 wei,这样就满足我们溢出的条件了,因为以太坊处理数据是以256位为单位,我们传入一个较大的numTokens,乘法运算溢出后所需的mag.value就非常小了
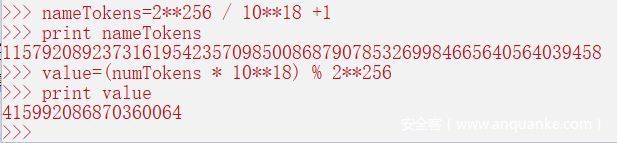
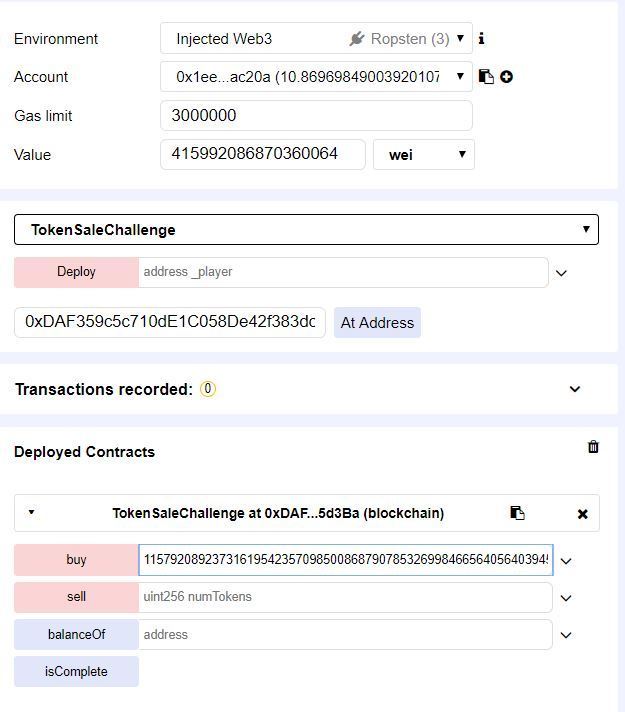
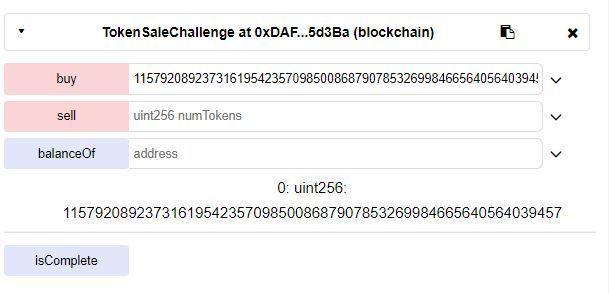
这里我们的numTokens就选择可以使该运算溢出的最小值,这样所需的value也最少,结果如下:
然后就可以去买token了
得到了巨多的token
然后sell 1个ether即可,毕竟也只能用这么多
0x2. Token whale
pragma solidity ^0.4.21;
contract TokenWhaleChallenge {
address player;
uint256 public totalSupply;
mapping(address => uint256) public balanceOf;
mapping(address => mapping(address => uint256)) public allowance;
string public name = "Simple ERC20 Token";
string public symbol = "SET";
uint8 public decimals = 18;
function TokenWhaleChallenge(address _player) public {
player = _player;
totalSupply = 1000;
balanceOf[player] = 1000;
}
function isComplete() public view returns (bool) {
return balanceOf[player] >= 1000000;
}
event Transfer(address indexed from, address indexed to, uint256 value);
function _transfer(address to, uint256 value) internal {
balanceOf[msg.sender] -= value;
balanceOf[to] += value;
emit Transfer(msg.sender, to, value);
}
function transfer(address to, uint256 value) public {
require(balanceOf[msg.sender] >= value);
require(balanceOf[to] + value >= balanceOf[to]);
_transfer(to, value);
}
event Approval(address indexed owner, address indexed spender, uint256 value);
function approve(address spender, uint256 value) public {
allowance[msg.sender][spender] = value;
emit Approval(msg.sender, spender, value);
}
function transferFrom(address from, address to, uint256 value) public {
require(balanceOf[from] >= value);
require(balanceOf[to] + value >= balanceOf[to]);
require(allowance[from][msg.sender] >= value);
allowance[from][msg.sender] -= value;
_transfer(to, value);
}
}
又是一道Token题,有了上一题的经验估计这题也是对溢出的利用,那么先来找找溢出点,粗略看一下很容易就发现_transfer函数没有进行溢出的检查,同时注意到它是个内部函数,那么我们来看看在哪可以调用它
transfer与transferFrom函数都可以调用该函数,transfer中对上溢进行了检查,显然不存在问题,重点在于这里的transferFrom函数,我们注意到它的require条件并没有针对msg.sender的balance进行检查,而其下面调用的_transfer函数中却会操作msg.sender的balance,不难发现此处应该是存在下溢的
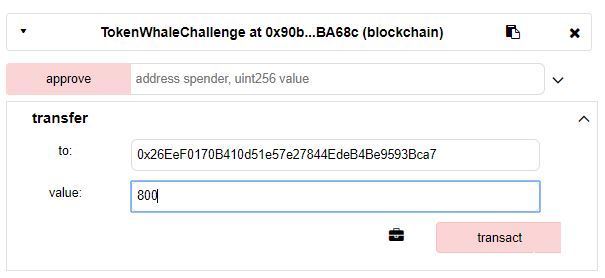
接下来我们的目标就是以player的身份调用transferFrom函数,看完代码后,我们发现要满足条件就需要有另一个地址来参与,并且需要其balance的值大于我们player的balance以满足下溢条件,这里我就用另一个account来完成测试,直接在metamask里新建即可,然后我们调用transfer函数给这个Account转balance,多少倒是随便,超过一半即可,700,800都行,总数是1000
然后我们调用approve来设置allowance,注意此时需要在metaMask切换到我们的Account 2,value的值也比较随意,只要比你想转的多就行,或者说比player的balance多即可
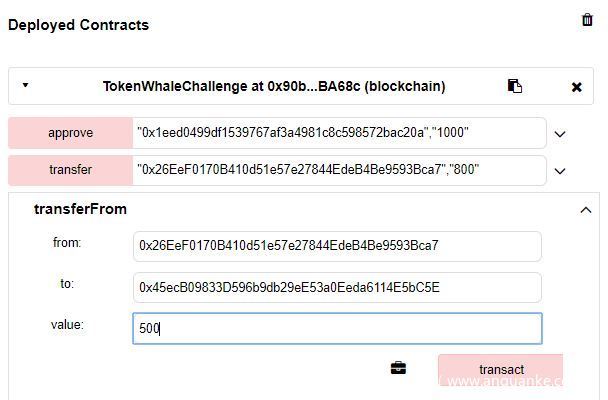
然后我们就能使用transferFrom函数了,此时切换回我们的player所在的Account,在from填上我们的Account 2,to这里其实随便填个地址即可,但不要是player地址,不然就白溢出了,这里我就选择了Account 3,value在Account 2的balance范围内选个比player的balance多的值即可
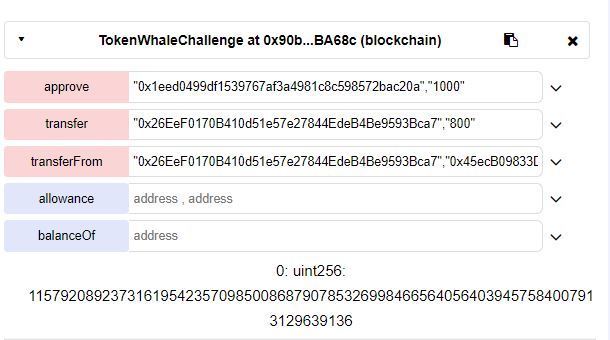
然后便拿到了数不完的balance,美滋滋
0x3. Retirement fund
pragma solidity ^0.4.21;
contract RetirementFundChallenge {
uint256 startBalance;
address owner = msg.sender;
address beneficiary;
uint256 expiration = now + 10 years;
function RetirementFundChallenge(address player) public payable {
require(msg.value == 1 ether);
beneficiary = player;
startBalance = msg.value;
}
function isComplete() public view returns (bool) {
return address(this).balance == 0;
}
function withdraw() public {
require(msg.sender == owner);
if (now < expiration) {
// early withdrawal incurs a 10% penalty
msg.sender.transfer(address(this).balance * 9 / 10);
} else {
msg.sender.transfer(address(this).balance);
}
}
function collectPenalty() public {
require(msg.sender == beneficiary);
uint256 withdrawn = startBalance - address(this).balance;
// an early withdrawal occurred
require(withdrawn > 0);
// penalty is what's left
msg.sender.transfer(address(this).balance);
}
}
这个挑战也有点意思,叫退休基金,介绍里说他要留1 ether养老并且上个锁保证自己10年内都不会取出来,如果他提前取出来的话就把存的钱留十分之一给你,不过这部署的过程花的不还是我的ether么,罢了,这些细节就不要在意了
很显然withdraw函数我们是无法调用的,我们只是个player,那么关注点自然就在collectPenalty,看起来它似乎是无法调用的,满足的条件里需要withdrawn大于零,但是这里startBalance与此合约的balance都是1 ether,那么withdrawn应该一直为0,然而遍寻合约也没见到可以发送ether的位置,事实上这里的考点是以太坊中合约的自毁机制,这是通过selfdestruct函数来实现的,如它的名字所显示的,这是一个自毁函数,当你调用它的时候,它会使该合约无效化并删除该地址的字节码,然后它会把合约里剩余的balance发送给参数所指定的地址,比较特殊的是这笔ether的发送将无视合约的fallback函数,所以它是强制性的,这样的话我们就有手段来修改当前合约的balance值了,更进一步我相信你也发现了此处下溢的存在,withdrawn > 0就成功被满足了
部署攻击合约:
contract attack {
address target = address of your challenge;
function attack() public payable {
}
function kill() public {
selfdestruct(target);
}
}
注意部署的时候要发送一些ether,不然自毁了也没balance可发,然后即可直接调用目标合约的collectPenalty完成挑战了
0x4. Mapping
pragma solidity ^0.4.21;
contract MappingChallenge {
bool public isComplete;
uint256[] map;
function set(uint256 key, uint256 value) public {
// Expand dynamic array as needed
if (map.length <= key) {
map.length = key + 1;
}
map[key] = value;
}
function get(uint256 key) public view returns (uint256) {
return map[key];
}
}
老实说刚看到这题我也有点摸不着头脑,代码倒是非常少,在这几关里应该是最短的了,目标肯定是要覆盖掉isComplete的值,显然利用点应该是在set函数里,开始时注重点放在了map.length上,因为这里的+1操作显然是存在溢出的,但是在本地测试过后我发现这里哪怕溢出也无法影响isComplete所在的存储位,不过在remix上的js虚拟机进行测试的时候倒是让我把目光转向了map键值的存储位
我们知道对于动态数组,其在声明中所在位置决定的存储位里存放的是其长度,而其中的变量的存储位则是基于其长度所在的存储进行,这部分的详细内容可以参见此处一篇翻译文章了解以太坊智能合约存储
现在我们知道了动态数组内变量所在的存储位的计算公式即为
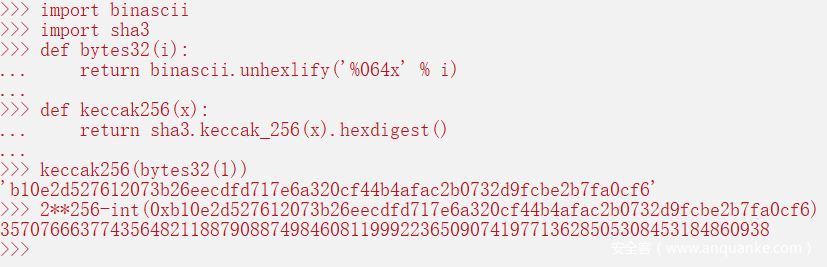
keccak256(slot) + index
slot是数组长度所在的存储位,我想你也猜到了,这个挑战里我们真正要利用的溢出其实是在这里,index是我们可控的,只要它够大我们就能够成功上溢,覆盖掉isComplete所在的0号存储位
首先计算map数组中第一个变量所在的存储位,然后计算溢出所需的index大小
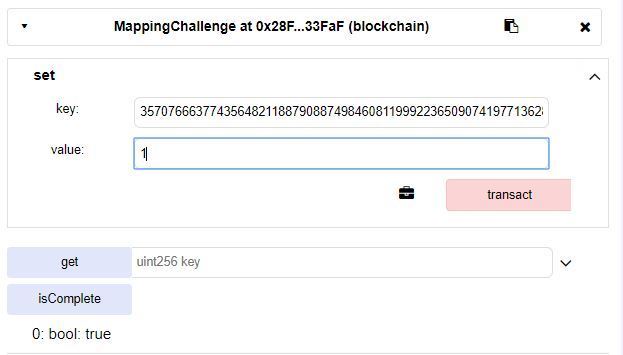
将此作为参数传递进set,value设为1即可
0x5. Donation
pragma solidity ^0.4.21;
contract DonationChallenge {
struct Donation {
uint256 timestamp;
uint256 etherAmount;
}
Donation[] public donations;
address public owner;
function DonationChallenge() public payable {
require(msg.value == 1 ether);
owner = msg.sender;
}
function isComplete() public view returns (bool) {
return address(this).balance == 0;
}
function donate(uint256 etherAmount) public payable {
// amount is in ether, but msg.value is in wei
uint256 scale = 10**18 * 1 ether;
require(msg.value == etherAmount / scale);
Donation donation;
donation.timestamp = now;
donation.etherAmount = etherAmount;
donations.push(donation);
}
function withdraw() public {
require(msg.sender == owner);
msg.sender.transfer(address(this).balance);
}
}
这一关的考点其实也挺有意思的,因为结构体在函数内非显式地初始化的时候会使用storage存储而不是memory,所以就可以达到变量覆盖的效果,关于这我也专门写过相关的文章,Solidity中存储方式错误使用所导致的变量覆盖,个人感觉写的还算清楚,这也是solidity的一个bug,官方是准备在0.5.0版本修复,不过看来是遥遥无期了
对这方面有了解的话其实一眼就能看出来玄机了,显然此处donate函数中初始化donation结构体的过程存在问题,我们可以覆盖solt 0和slot 1处1存储的状态变量,恰好solt 1存储的即为owner,而覆盖其位置需要的etherAmount又是我们可控的,那么现在的目标就是传入正确的etherAmount来调用donate函数从而覆盖owner为我们的Account地址
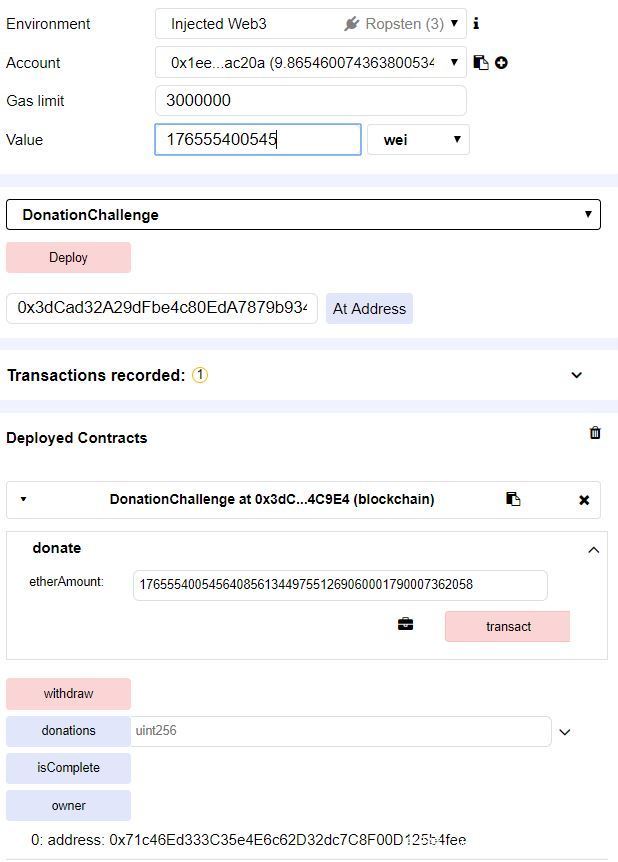
对于传入的etherAmount,其值只要等于我们的Account地址即可,然后满足下面的对于msg.value的要求,简单地计算一下即可得到结果
然后我们使用这些参数调用donate函数,此时owner变量还是另一个地址
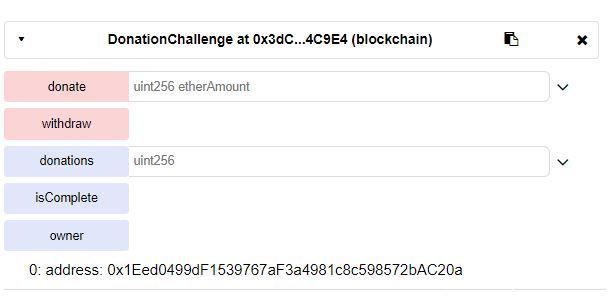
成功将自己的Account改写为owner
然后调用withdraw函数拿钱走人
0x6. Fifty years
pragma solidity ^0.4.21;
contract FiftyYearsChallenge {
struct Contribution {
uint256 amount;
uint256 unlockTimestamp;
}
Contribution[] queue;
uint256 head;
address owner;
function FiftyYearsChallenge(address player) public payable {
require(msg.value == 1 ether);
owner = player;
queue.push(Contribution(msg.value, now + 50 years));
}
function isComplete() public view returns (bool) {
return address(this).balance == 0;
}
function upsert(uint256 index, uint256 timestamp) public payable {
require(msg.sender == owner);
if (index >= head && index < queue.length) {
// Update existing contribution amount without updating timestamp.
Contribution storage contribution = queue[index];
contribution.amount += msg.value;
} else {
// Append a new contribution. Require that each contribution unlock
// at least 1 day after the previous one.
require(timestamp >= queue[queue.length - 1].unlockTimestamp + 1 days);
contribution.amount = msg.value;
contribution.unlockTimestamp = timestamp;
queue.push(contribution);
}
}
function withdraw(uint256 index) public {
require(msg.sender == owner);
require(now >= queue[index].unlockTimestamp);
// Withdraw this and any earlier contributions.
uint256 total = 0;
for (uint256 i = head; i <= index; i++) {
total += queue[i].amount;
// Reclaim storage.
delete queue[i];
}
// Move the head of the queue forward so we don't have to loop over
// already-withdrawn contributions.
head = index + 1;
msg.sender.transfer(total);
}
}
这道题的分值目前是所有挑战里最高的,达到了2000分,也确实花了我不少时间,质量还是挺高的
整个代码想传达的主要规则很简单,你可以向整个贡献队列里添加条目,amount即为你发送的ether,但是之后的时间锁会将这些amount锁在合约里,只有过了规定的时间之后才能全部提取出来,同时第一个amount也就是我们创建合约时存入的1 ether,之后添加的每一条都必须在其前一个contribution的时间锁的基础上增加一天的时间,第一个contribution的时间锁为50年以后,如果你等够50年的话倒是能直接完成这个挑战。。。
要成功提取合约内的所有balance只能通过withdraw函数,也就是要绕过其时间锁的限制,突破点肯定在upsert函数内,很容易地注意到此函数里使用了storage存储来初始化一个contribution结构体,这势必会造成变量覆盖,道理跟前面的Donation那道题目一样,这样的话可被我们覆盖的值就包括queue的长度与head的值,在这可能还看不出来覆盖queue长度的作用,因为在前面我们知道这无法对其它存储位上的变量造成影响
往下看,看到这一句
queue.push(contribution);
这一行将在queue里增加我们前面初始化的这一contribution,然后我就想是否是这插入的位置的玄机,因为queue是个动态数组,其中的变量所在的存储位计算规则为
keccak256(slot) + index * elementsize
这里elementsize即为结构体Contribution的size 2,push更新queue的存储使用的自然也是这个公式,那么其使用的index应该就是queue的length了,关于这可以验证,我就懒得贴图了,而queue.length是我们可控的,这方面肯定可以做点文章
这样的话梳理一下,我们现在就可以使用msg.value来决定我们要增加的对象所在的存储位,当然这种情况下你得先让index大于queue.length才能触发增加对象的条件,但是我们的目标还是调用withdraw啊,它最关键的限制在这里
require(now >= queue[index].unlockTimestamp);
前面我们也提到了第一个contribution的时间锁就是五十年,之后每个必须至少比前面一项多一天,这个限制是由下面这行代码附加的
require(timestamp >= queue[queue.length – 1].unlockTimestamp + 1 days);
经历了前面这么多挑战是不是感觉套路很眼熟,没错,这里显然又是存在上溢的,如果前面一个对象的时间锁加上一天以后溢出为0,那么我们增加的项目的时间锁就可以设置为0了,这一点很重要,因为head的值是会被我们增加的对象的时间锁给覆盖的,如果不设为0,在下面调用withdraw时就会从非0位开始提取balance,从而无法覆盖到我们必须提取的queue[0]的那1 ether
因为1 days的值为86400,我们直接计算溢出所需的时间锁大小
2**256-86400
115792089237316195423570985008687907853269984665640564039457584007913129553536
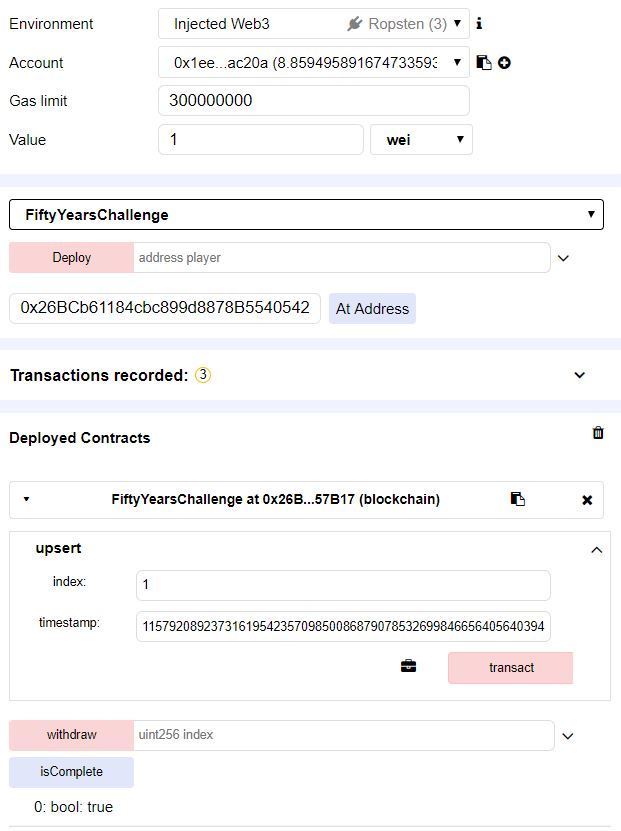
这样的话按我一开始的想法接下来应该很简单了,先在queue的index 1处添加一个记录,时间锁就传递我们上面计算得到的值,然后在queue的index 2处添加一个记录,时间锁传递为0,这两步操作通过发送1 wei和2 wei来调用upsert函数即可实现,然后我们的head值就被设为0了,这样的话我们应该就满足调用withdraw的条件了,但是尝试了一下你就会发现依然是调用失败,在本地测试时可以debug一下,发现问题是出在最后一步进行transfer的时候,这可让人难受死了,都到最后关头了还是过不去
如果你是在本地环境上测试的话应该不难发现在每次增加对象后事实上新的contribution的amount值并不是我们传递的msg.value的值,在其基础上还加了1.开始我也不太明白,后来debug发现原来queue.length也是msg.value+1,因为二者共用一块存储,应该是queue.length增加时也修改了amount的值,至于此处queue.length为何+1,则是因为queue.push操作,因为其在最后执行增添对象的任务,添加以后它会将queue.length进行+1操作
这样一切就解释的通了,关键就是这里amount进行了+1,所以在withdraw是所统计的total事实上是大于合约所拥有的balance,所以transfer无法执行,这一点确实有点难到我了,必须想个办法抵消这一步+1的操作
很快,我意识到我可以利用value来覆盖已有的contribution,既然发1 wei会加1,那我发两次,这样得到的amount就是2,也就是我实际发送的wei数目,所以把上面那两步写入操作都改成1 wei下的操作即可
第一步
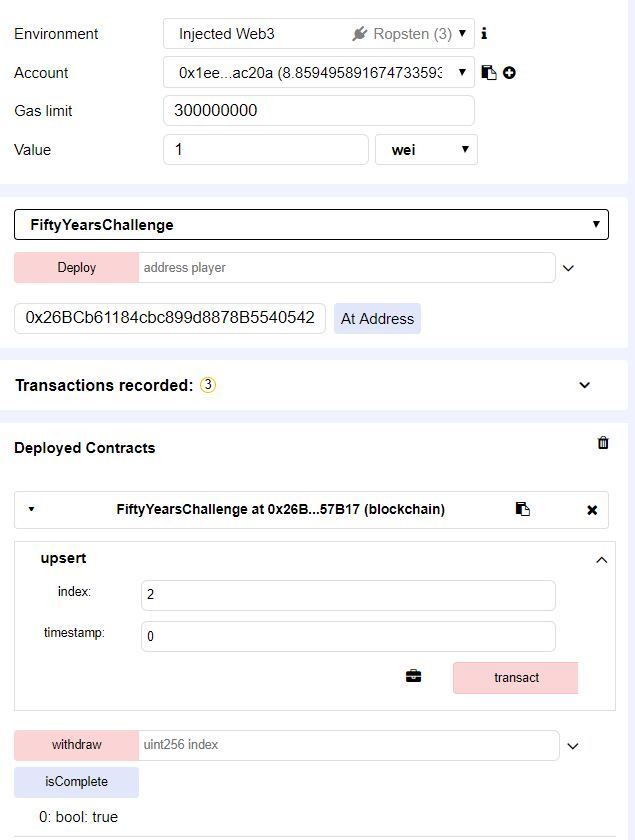
第二步
然后调用withdraw(1)即可成功通关
总的来说这一关还是非常有意思的,很推荐自己动手试试,只是看文字可能不是很好体会