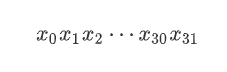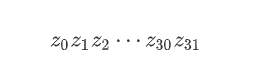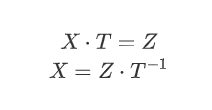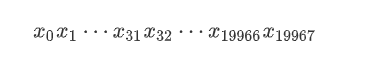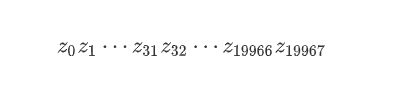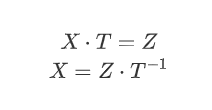引言
近年来MT19937在各大CTF赛事中出现的频率越来越高,本文主要讨论CTF中的常见的MT相关问题,并利用几道典型的赛题进行实战分析,尤其是今年二月份pwnhub的一道零解题(详见扩展题型)。感谢zzh师傅的细心指点,赛后才勉强解出了这道CoinFlip2。
前置知识
MT19937是一种周期很长的的伪随机数生成算法,可以快速的产生高质量的伪随机数,主要分为三部分。
如果读者对该算法不了解,可以先参考wiki
1.利用seed初始化624的状态
2.对状态进行旋转
3.根据状态提取伪随机数
32位的MT19937的python代码如下:
def _int32(x):
return int(0xFFFFFFFF & x)
class MT19937:
# 根据seed初始化624的state
def __init__(self, seed):
self.mt = [0] * 624
self.mt[0] = seed
self.mti = 0
for i in range(1, 624):
self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)
# 提取伪随机数
def extract_number(self):
if self.mti == 0:
self.twist()
y = self.mt[self.mti]
y = y ^ y >> 11
y = y ^ y << 7 & 2636928640
y = y ^ y << 15 & 4022730752
y = y ^ y >> 18
self.mti = (self.mti + 1) % 624
return _int32(y)
# 对状态进行旋转
def twist(self):
for i in range(0, 624):
y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))
self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]
if y % 2 != 0:
self.mt[i] = self.mt[i] ^ 0x9908b0df
python中内置的Random类就是采用了MT19937算法,getrandbits(32)方法可以获得一个32位随机数
题型1 逆向 extract_number
首先分析extract_number函数,可以发现输出的伪随机数是对state[i]进行了异或,位运算后的结果。
逐步分析extract_number
y = y ^ (y >> 18)
我们可以发现这一步的运算对操作数y的高18位并没有产生影响,也就是说运算结束后y1 = y ^ ( y>> 18),得到y1高18位其实就是y的高18位,那么我们就可以得到y>>18的高36位,进而得到y1的高36位,也就是说我们可以在有限步内,获得y的所有信息,即我们可以根据y1逆向y。代码如下:
o = 2080737669
y = o^o>>18
# 控制位移的次数
for i in range(32//18):
y = y^(y>>18)
print(y==o)
我们可以发现逆向的过程和正向的过程惊人的相似,不得不感叹数学的奇妙。
继续分析
y = y ^ y << 15 & 4022730752
可以看到这一步位移的方向发生改变,而且增加了掩码,根据运算符的优先级,可以得到
y1 = y^((y<<15)&4022730752),实际上增加的掩码并没有太大的作用,因为y1的低15位实际上就是y的低15位和4022730752的低15位异或运算的结果,我们只需要y1^4022730752便可以得到y的低15位,于是得到y<<15的低30位,同理可以得到y1的低30位,经过有限步,最终可以得到y的全部信息。代码如下:
o = 2080737669
y = o ^ o << 15 & 4022730752
tmp = y
for i in range(32 // 15):
# (y<<15)&40022730752 每次可以恢复y的15位
y = tmp ^ y << 15 & 4022730752
print(y==o)
剩下的两步操作,可以采用同样的分析方法进行逆行。最终完整的代码如下:
o = 2080737669
# right shift inverse
def inverse_right(res, shift, bits=32):
tmp = res
for i in range(bits // shift):
tmp = res ^ tmp >> shift
return tmp
# right shift with mask inverse
def inverse_right_mask(res, shift, mask, bits=32):
tmp = res
for i in range(bits // shift):
tmp = res ^ tmp >> shift & mask
return tmp
# left shift inverse
def inverse_left(res, shift, bits=32):
tmp = res
for i in range(bits // shift):
tmp = res ^ tmp << shift
return tmp
# left shift with mask inverse
def inverse_left_mask(res, shift, mask, bits=32):
tmp = res
for i in range(bits // shift):
tmp = res ^ tmp << shift & mask
return tmp
def extract_number(y):
y = y ^ y >> 11
y = y ^ y << 7 & 2636928640
y = y ^ y << 15 & 4022730752
y = y ^ y >> 18
return y&0xffffffff
def recover(y):
y = inverse_right(y,18)
y = inverse_left_mask(y,15,4022730752)
y = inverse_left_mask(y,7,2636928640)
y = inverse_right(y,11)
return y&0xffffffff
y = extract_number(o)
print(recover(y) == o)
上述讨论的部分是,基于对extract_number函数的观察得到的逆向方法,除此之外我们还可以从extract_number的运算本质上进行逆向。
设state[i]的二进制表示形式为:
输出的随机数二进制形式为:
而z和x具有如下线性关系:
也就是说
其中X,Z是GF(2)上的1 x 32的向量,T是GF(2)上的 32 x 32的矩阵。我们只需要在GF(2)上求解X即可。已知Z,如果T也已知,可以快速的求解出X。那么如何计算T呢?
实际上我们可以采用黑盒测试的方法,猜解T。例如当X为(1,0,0,0,…..0)时,经过T得到的Z其实就是T中第一行。采用这种类似选择明文攻击的方法,我们可以得到T矩阵的每一行,进而还原T。最后再利用T和Z得到原始的X。代码如下:
# sagemath 9.0
from sage.all import *
from random import Random
def buildT():
rng = Random()
T = matrix(GF(2),32,32)
for i in range(32):
s = [0]*624
# 构造特殊的state
s[0] = 1<<(31-i)
rng.setstate((3,tuple(s+[0]),None))
tmp = rng.getrandbits(32)
# 获取T矩阵的每一行
row = vector(GF(2),[int(x) for x in bin(tmp)[2:].zfill(32)])
T[i] = row
return T
def reverse(T,leak):
Z = vector(GF(2),[int(x) for x in bin(leak)[2:].zfill(32)])
X = T.solve_left(Z)
state = int(''.join([str(i) for i in X]),2)
return state
def test():
rng = Random()
# 泄露信息
leak = [rng.getrandbits(32) for i in range(32)]
originState = [i for i in rng.getstate()[1][:32]]
# 构造矩阵T
T = buildT()
recoverState = [reverse(T,i) for i in leak]
print(recoverState==originState)
test()
这里的黑盒测试思想,会在后面的题型x,得到应用。希望读者理解后再继续阅读
题型2 预测随机数
这一类题型是基于对extract_number 函数的逆向,而发展来的。这里以2020年网鼎杯白虎组的random为例
2020网鼎杯白虎组random
定位到关键函数
def generate():
fw = open("random", "w")
for i in range(700):
fw.write(str(random.getrandbits(32))+"n")
fw.close()
generate()
f = open("flag.txt", "w")
key = str(random.getrandbits(32))
ciphertext = encryption(flag, key)
f.write(ciphertext)
f.close()
可以发现加密的key时第701个随机数,而且我们已知前700个随机数。于是可以根据输出的随机数逆向extract_number得到对应的700个state,实际上只需要前624个随机数恢复前624个state,就可以预测此后生成的随机数。代码如下:
# -*- coding: utf-8 -*-
from random import Random
def invert_right(m,l,val=''):
length = 32
mx = 0xffffffff
if val == '':
val = mx
i,res = 0,0
while i*l<length:
mask = (mx<<(length-l)&mx)>>i*l
tmp = m & mask
m = m^tmp>>l&val
res += tmp
i += 1
return res
def invert_left(m,l,val):
length = 32
mx = 0xffffffff
i,res = 0,0
while i*l < length:
mask = (mx>>(length-l)&mx)<<i*l
tmp = m & mask
m ^= tmp<<l&val
res |= tmp
i += 1
return res
def invert_temper(m):
m = invert_right(m,18)
m = invert_left(m,15,4022730752)
m = invert_left(m,7,2636928640)
m = invert_right(m,11)
return m
def clone_mt(record):
state = [invert_temper(i) for i in record]
gen = Random()
gen.setstate((3,tuple(state+[0]),None))
return gen
f = open("random",'r').readlines()
prng = []
for i in f:
i = i.strip('n')
prng.append(int(i))
g = clone_mt(prng[:624])
for i in range(700):
g.getrandbits(32)
key = g.getrandbits(32)
print(key)
#2990136190
代码中逆向extract_number 部分的invert_right函数和题型1中的代码不同,但是效果是相同的(很久之前写的,所以直接粘过来了。)得到key之后就是常规的des解密,最后可以得到flag。
题型3 逆向twist
在已知连续624个随机数时(state没有进行twist),可以还原state,预测后续的随机数。那么如何获得624个随机数之前的随机数呢?此时可以考虑,逆向twist获得前一组的state,进而获得前一组的624个随机数。
首先看一下twist函数
def twist(self):
for i in range(0, 624):
y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))
self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]
if y % 2 != 0:
self.mt[i] = self.mt[i] ^ 0x9908b0df
考虑下面的例子:
1. 11100110110101000100101111000001 // state[i]
2. 10101110111101011001001001011111 // state[i + 1]
3. 11101010010001001010000001001001 // state[i + 397]
// y = state[i] & 0x80000000 | state[i + 1] & 0x7fffffff
4. 10101110111101011001001001011111 // y
5. 01010111011110101100100100101111 // next = y >>> 1
6. 11001110011100100111100111110000 // next ^= 0x9908b0df
0x9908b0df => 10011001000010001011000011011111
7. 00100100001101101101100110111001 // next ^= state[i + 397]
我们知道生成新的state[i]只与原来的state[i],state[i+1],state[i+397]有关。第7步是必须进行的一步(异或的次序不影响结果,所以异或state[i+397]可以看成最后一步),第6步是根据第4步结果的奇偶性确定的,不一定有第6步,但是因为第7步是第5步或者第6步异或state[i+397]的结果,我们可以考察新生成的state[i]异或state[i+397]的结果,来判断是否进行了第六步的操作。
由于0x9908b0df => 10011001000010001011000011011111,而第5步的最高位必定是0,但是如果执行了第6步那么执行后的结果首位则会变成1,于是我们可以根据第7步逆向出的结果的首位判断是否进行了第6步.进而推出第5步,第5步的后31位包含了state[i]的第1位和state[i+1]的第2位至第31位,根据第6步是否进行可以得到state[i+1]的最后1位,所以根据现在的state[i]和以前的state[i+397],可以获得原来state[i]的1位信息和state[i+1]的31位信息,要获得state[i]剩下的31位信息,需要对现在的state[i-1]进行同样的运算.当需要计算第一位state时,剩下的state都已经恢复了,可以利用恢复了的最后一位state获得还未恢复的state[0]的后31位,非常巧妙!
实现代码如下:
def backtrace(cur):
high = 0x80000000
low = 0x7fffffff
mask = 0x9908b0df
state = cur
for i in range(623,-1,-1):
tmp = state[i]^state[(i+397)%624]
# recover Y,tmp = Y
if tmp & high == high:
tmp ^= mask
tmp <<= 1
tmp |= 1
else:
tmp <<=1
# recover highest bit
res = tmp&high
# recover other 31 bits,when i =0,it just use the method again it so beautiful!!!!
tmp = state[i-1]^state[(i+396)%624]
# recover Y,tmp = Y
if tmp & high == high:
tmp ^= mask
tmp <<= 1
tmp |= 1
else:
tmp <<=1
res |= (tmp)&low
state[i] = res
return state
2020 V&N 招新赛 Backtrace
# !/usr/bin/env/python3
import random
flag = "flag{" + ''.join(str(random.getrandbits(32)) for _ in range(4)) + "}"
with open('output.txt', 'w') as f:
for i in range(1000):
f.write(str(random.getrandbits(32)) + "n")
print(flag)
题目信息很简练,我们需要恢复前四个随机数。我们需要连续的624个随机数才能获得上一组随机数的状态,这里只有1000个随机数,但是之后前4位丢失,而前4位产生的新状态对应第624,625,626,627位随机数的状态,而他们的状态是可逆的。所以不需要完整的连续624个随机数,也可以求解完整的state。代码如下:
#!/usr/bin/python3
from random import Random
# right shift inverse
def inverse_right(res,shift,bits=32):
tmp = res
for i in range(bits//shift):
tmp = res ^ tmp >> shift
return tmp
# right shift with mask inverse
def inverse_right_values(res,shift,mask,bits=32):
tmp = res
for i in range(bits//shift):
tmp = res ^ tmp>>shift & mask
return tmp
# left shift inverse
def inverse_left(res,shift,bits=32):
tmp = res
for i in range(bits//shift):
tmp = res ^ tmp << shift
return tmp
# left shift with mask inverse
def inverse_left_values(res,shift,mask,bits=32):
tmp = res
for i in range(bits//shift):
tmp = res ^ tmp << shift & mask
return tmp
def backtrace(cur):
high = 0x80000000
low = 0x7fffffff
mask = 0x9908b0df
state = cur
for i in range(3,-1,-1):
tmp = state[i+624]^state[i+397]
# recover Y,tmp = Y
if tmp & high == high:
tmp ^= mask
tmp <<= 1
tmp |= 1
else:
tmp <<=1
# recover highest bit
res = tmp&high
# recover other 31 bits,when i =0,it just use the method again it so beautiful!!!!
tmp = state[i-1+624]^state[i+396]
# recover Y,tmp = Y
if tmp & high == high:
tmp ^= mask
tmp <<= 1
tmp |= 1
else:
tmp <<=1
res |= (tmp)&low
state[i] = res
return state
def recover_state(out):
state = []
for i in out:
i = inverse_right(i,18)
i = inverse_left_values(i,15,0xefc60000)
i = inverse_left_values(i,7,0x9d2c5680)
i = inverse_right(i,11)
state.append(i)
return state
f = open("output.txt","r").readlines()
c = []
for i in range(1000):
c.append(int(f[i].strip()))
partS = recover_state(c)
state = backtrace([0]*4+partS)[:624]
# print(state)
prng = Random()
prng.setstate((3,tuple(state+[0]),None))
flag = "flag{" + ''.join(str(prng.getrandbits(32)) for _ in range(4)) + "}"
print(flag)
题型4 逆向init
其实这一部分还没有出现过类似的题目,这里就我的理解,简单的叙述一下。
前文分别叙述了,根据输出逆向对应的state,以及根据输出逆向上一组的state。此部分则是根据第一次的state,逆向seed。
首先看一下,init函数
def _int32(x):
return int(0xFFFFFFFF & x)
def init(seed):
mt = [0] * 624
mt[0] = seed
for i in range(1, 624):
mt[i] = _int32(1812433253 * (mt[i - 1] ^ mt[i - 1] >> 30) + i)
return mt
定位到关键函数mt[i] = _int32(1812433253 * (mt[i - 1] ^ mt[i - 1] >> 30) + i),可以发现其中的(mt[i - 1] ^ mt[i - 1] >> 30)是可逆的(详见题型1),注意到_int32其实相当于取低32位,相当于mod 2^32。而gcd(1812433253,2**32) == 1于是1812433253存在逆元。那么逆向的过程其实就是模逆操作再组合上题型1的操作,便可以得到seed。代码如下:
from gmpy2 import invert
def _int32(x):
return int(0xFFFFFFFF & x)
def init(seed):
mt = [0] * 624
mt[0] = seed
for i in range(1, 624):
mt[i] = _int32(1812433253 * (mt[i - 1] ^ mt[i - 1] >> 30) + i)
return mt
seed = 2080737669
def invert_right(res,shift):
tmp = res
for i in range(32//shift):
res = tmp^res>>shift
return _int32(res)
def recover(last):
n = 1<<32
inv = invert(1812433253,n)
for i in range(623,0,-1):
last = ((last-i)*inv)%n
last = invert_right(last,30)
return last
state = init(seed)
print(recover(state[-1]) == seed)
扩展题型
在题型2中我们采用的黑盒测试的方法,找到了状态和输出的转移矩阵T。这是因为每个状态的二进制位与其输出的随机数的二进制位,存在线性关系。而每次twist后新生成的状态都是前一组状态的线性组合,也就是说任意一组状态都是第一组状态的线性组合。那么由任意一组状态生成的伪随机数的二进制位和第一组状态的二进制位存在线性关系。
不妨设 初始状态的二进制形式为:
设19968个伪随机数的MSB (注意这里不要求一定是MSB,可以是随机数的任意二进制位,也不一定要求是19968个随机数,只要能构成19968个二进制位即可)构成的向量为:
于是有在GF(2)上有如下等式,其中X,Z为1 x 19968 的向量,T为19968 x 19968 的矩阵:
采用题型2中同样的方法,对T进行黑盒测试。即设置X(1,0,0,0,…0)得到Z为T的第一行,遍历所有情况得到T。最后还原出X。
2020 pwnhub CoinFlip2
#!/usr/bin/env -S python3 -u
import random
count = 0
while True:
print("Progress: %s/50" % count)
coin = random.getrandbits(1)
if int(input("Your guess: ")) == coin:
print("Correct!")
count += 1
if count == 50:
print(open("flag").read())
exit()
else:
print("Wrong!")
count = 0
python中的getrandbits(1)其实截取的是getrandbits(32)的最高位即MSB。于是我们需要收集19968个MSB,并构造T,才能还原state。需要注意的是这里构造的T并不是满秩的,但是sage仍然可以求解,不过求解得到的X的前32位,并不正确。但是我们仍然能够得到623位的state,我们可以利用题型3中的方法还原第一位state。进而利用state预测接下来的随机数。不过需要注意的是,构造矩阵T是相当耗费时间的,笔者在2h2g的机器上跑了大约一个多小时,才算出结果。为了读者的方便,这里直接给出矩阵的数据
坚果云(需要注册,但速度很快访问密码 : badmonkey)
具体代码如下,可以根据需要更改:
#! /bin/bash/env python3
from sage.all import *
from random import Random
from tqdm import tqdm
prng = Random()
length = 19968
def myState():
state = [0]*624
i = 0
while i<length:
ind = i//32
expont = i%32
state[ind] = 1<<(31-expont)
s = (3,tuple(state+[0]),None)
yield s
state[ind] = 0
i += 1
def getRow():
rng = Random()
gs = myState()
for i in range(length):
s = next(gs)
rng.setstate(s)
# print(s[1][0])
row = vector(GF(2),[rng.getrandbits(1) for j in range(length)])
yield row
def buildBox():
b = matrix(GF(2),length,length)
rg = getRow()
for i in tqdm(range(length)):
b[i] = next(rg)
return b
def test():
prng = Random()
originState = prng.getstate()
# 这里都是用的MSB,如果采用不同的二进制位(如LSB)最后的矩阵T 也会不同
leak = vector(GF(2),[prng.getrandbits(1) for i in range(length)])
b = buildBox()
f = open("Matrix","w")
for i in range(b.nrows()):
for j in range(b.ncols()):
f.write(str(b[i,j])+"n")
f.close()
x = b.solve_left(leak)
x = ''.join([str(i) for i in x])
state = []
for i in range(624):
tmp = int(x[i*32:(i+1)*32],2)
state.append(tmp)
prng.setstate(originState)
prng.getrandbits(1)
originState = [x for x in prng.getstate()[1][:-1]]
print(originState[1:] == state[1:])
# print(state)
return state,b
test()
利用脚本如下:
from sage.all import *
from random import Random
from tqdm import tqdm
# 根据文件中的信息,构造矩阵
def buildMatrix():
length = 19968
cnt = 0
m = matrix(GF(2), length, length)
for line in tqdm(open("Matrix", "r")):
row = cnt // 19968
col = cnt % 19968
m[row, col] = int(line.strip('n'))
cnt += 1
return m
m = buildMatrix()
# X = Z*(T^-1)
def recoverState(leak):
x = m.solve_left(leak)
x = ''.join([str(i) for i in x])
state = []
for i in range(624):
tmp = int(x[i * 32:(i + 1) * 32], 2)
state.append(tmp)
return state
# 根据题型2,还原state,有两种可能,这时候可以用暴破
def backfirst(state):
high = 0x80000000
low = 0x7fffffff
mask = 0x9908b0df
tmp = state[623] ^ state[396]
if tmp & high == high:
tmp ^= mask
tmp <<= 1
tmp |= 1
else:
tmp <<= 1
return (1 << 32 - 1) | tmp & low, tmp & low
def pwn(leak):
state = recoverState(leak)
L = [leak[i] for i in range(100)]
prng = Random()
guess1, guess2 = backfirst(state)
print(guess1, guess2)
state[0] = guess1
s = state
prng.setstate((3, tuple(s + [0]), None))
g1 = [prng.getrandbits(1) for i in range(100)]
if g1 == L:
print("first")
prng.setstate((3, tuple(s + [0]), None))
return prng
state[0] = guess2
s = state
prng.setstate((3, tuple(s + [0]), None))
g2 = [prng.getrandbits(1) for i in range(100)]
if g2 == L:
print("second")
prng.setstate((3, tuple(s + [0]), None))
return prng
def test():
length = 19968
prng = Random()
originState = prng.getstate()
leak = vector(GF(2), [prng.getrandbits(1) for i in range(length)])
# 恢复state
state = recoverState(leak)
prng.setstate(originState)
prng.getrandbits(1)
originState = [x for x in prng.getstate()[1][:-1]]
# 成功恢复623个state
print(originState[1:] == state[1:])
# 获取泄露信息
L = [leak[i] for i in range(100)]
# 两种可能
guess1, guess2 = backfirst(state)
print(guess1, guess2)
state[0] = guess1
s = state
prng.setstate((3, tuple(s + [0]), None))
g1 = [prng.getrandbits(1) for i in range(100)]
if g1 == L:
print("first")
prng.setstate((3, tuple(s + [0]), None))
now = vector(GF(2), [prng.getrandbits(1) for i in range(length)])
if now == leak:
print("true")
return
state[0] = guess2
s = state
prng.setstate((3, tuple(s + [0]), None))
g2 = [prng.getrandbits(1) for i in range(100)]
if g2 == L:
print("second")
prng.setstate((3, tuple(s + [0]), None))
now = vector(GF(2), [prng.getrandbits(1) for i in range(length)])
if now == leak:
print("true")
return
test()
大概需要6-7分钟可以构建完矩阵。
结语
本人水平有限,如有错误欢迎指出,希望大家能从中学到一些东西。