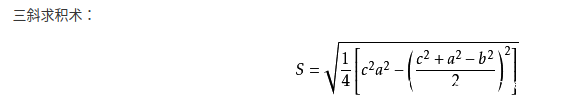0ctf 2019的一道逆向题
题目逆向
先拖进ida简单看一下,又是典型的输入flag过check的逆向题。如果通过check则输出Congratz。我们一个一个检查看:
检查1
首先是一个常规的检查,读取输入,然后检查输入的长度是0x2c,检查输入是否以flag{开头,以}结尾。
检查2
之后对输入掐头去尾,对中间剩余的内容用-来分割,得到一个字符串序列。之后会解析这个序列里的每一个元素,检查其长度是否为12,把字符串转化为对应的数字,比如把字符串dead转化为数字0xdead,即57005。此外,如果是序列中的第一个元素,会判定其是否是一个特定值0x391bc2164f0a,代码如图:
因此我们可以得到flag的第一部分就是391bc2164f0a
检查3
检查3是最复杂的部分。首先程序会把之前从字符串解析出来的数字做一个转换:
这个转换用了一些奇怪的API,我们先不管。
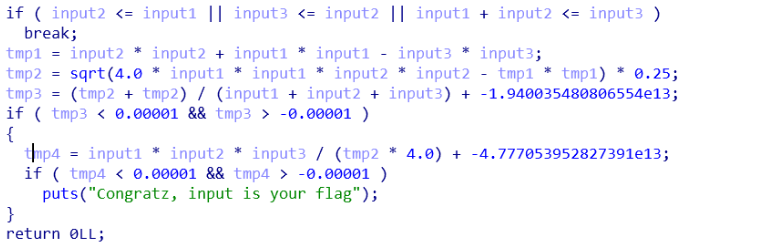
当解析了3个序列之后会进入检查3,代码如图:
input1,input2,input3分别是我们输入的3个序列,其中input1已知。首先会对三个序列的大小关系做了一个比较,然后对这三个序列做了一系列复杂的运算,包括开根号和浮点数运算,最后得到两个浮点数的值tmp3和tmp4,如果这两个值分别是1.94003…和4.77705….则通过检查。
虽然现在我们只有两个未知数和两个等式,但是这并不是一次方程,运算过程中有平方和开根号,可以尝试用平方消去根号,最后得到了一个四次方程,很难直接求出input2和input3
三角函数公式和三斜求积术
我们大胆猜测,题目所做的运算应该不是无意义随便构造出来的,而是有其物理/数学意义的。经过一些搜索,我们发现tmp2进行的运算,实际是秦九韶公式,或称为三斜求积术,是海伦公式的一种等价表示。
对于三角形三边a,b,c;其中c为最长边,a为最短边,则三角形的面积S可以表示为:
在题目中,根据check3中一开始对三个值的比较可知input1是最短边(a),input3是最长边(c)。tmp2是三角形面积S。这样我们可以把tmp3和tmp4改写为:
tmp3 = 2S/(a+b+c)
tmp4 = abc/(4*S)
根据三角函数的相关知识我们可以知道tmp3表示三角形内切圆半径,tmp4表示三角形外接圆半径。
tmp3 = 2S/(a+b+c)=r
tmp4 = abc/(4*S)=R
题目转化为已知三角形最短边a以及三角形外接圆半径R和三角形内切圆r,求三角形的其他两边。
列出方程
下面就要列方程解这个三角函数问题。
首先利用正弦定理
a/sin A = 2*R
得到
sin A = a/(2R)
根据余弦定理,
cos A = (b^2+c^2-a^2)/(2bc)= sqrt(1-(sin A)^2)
联立上述多个等式得到
4Rr(1+cosA)/a = T1 = 4 * tmp3 * tmp4 *(b^2+c^2-a^2+2bc)/2bc =(abc) * (b+c+a) * (b+c-a)/(a * bc * (a+b+c)) = b + c - a
即 b + c = a + T1 = T2
之后联立两个面积公式得到
S = abc/4R = (a + b + c)r/2
abc = 2Rr(a+b+c)=2Rr(a+T2)
bc= 2Rr(a+T2)/a = T3
得bc后计算c-b,并得到最终的解
c-b = sqrt((c+b)^2 - 4bc) = sqrt(T2^2-4T3) = T4
c = (T2+T4)/2
b = (T2-T4)/2
解题脚本
from math import sqrt
r = 1.940035480806554e13
R = 4.777053952827391e13
a = 62791383142154.0
sinA = a / (2.0 * R)
cosA2 = 1 - sinA**2
cosA = sqrt(cosA2)
T2 = a+4*R*r*(1+cosA)/a#b+c
T3 = 2*R*r*(a+T2)/a #bc
T4 = sqrt(T2*T2-4*T3)#c-b
c = int((T2+T4)/2)
b = int((T2-T4)/2)
print c
print b
这个脚本算的b和c会有一些精度的丢失,我们可以手动调整一下b和c的个位,输到程序里检查b和c是否正确。
最后得到flag{391bc2164f0a-4064e4798769-56e0de138176}