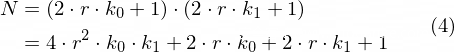前言
DEF CON CTF Quals 2020中共有三道CRYPTO方向题目(两道CRYPTO、一道RE+CRYPTO),题目难度适中,比赛期间三道题目都出现了非预期解,本文对这三道题目的预期解和非预期解都进行一下分析。
coooppersmith
题目描述
I was told by a cooopersmith that I should send hackers encrypted messages because it is secure.
coooppersmith.challenges.ooo 5000130/500 pts, 41 solves
解题思路
本题程序要求选手输入一个长度不超过120的16进制串,然后会以PEM格式打印RSA公钥,并在"Question"字符串下一行打印了一个16进制串,最后接收一个用户输入:
Please input prefix IN HEX with length no more than 120: deadbeef
Your public key:
-----BEGIN RSA PUBLIC KEY-----
MIIBCQKCAQA72hJsgSuPfUh1+EVHJMilCiEw5W5IiWOjdfRnuqdn2rsuvJSazeUg
3X0MITlZbIgM9oh7KP3uk6cGjF1HyOI1eAE4Yf8zLXHfVbFg5cx5ZcIJ7twrFgIV
Bz8kwTim8nt1bNf3AwPXpMJFr23BLMV6qaAGFcoffxgcEVz6hrHZDJYDXRfDlLGN
8a2x2w45dTLy53HR5GKV4xE4JoY9bJp7zmdJ/AVPD241XcHxDCaYh6qKeOjPAXLM
MJXR4qjHNfOJ9clzn57+V0553dPOkwsTdhtnjLo1lCuNurHinfiqQgpvJF4p7T2R
n3YE9HhPghwbiX6wwunBP4x5qI0qn47hAgMBAAE=
-----END RSA PUBLIC KEY-----
Question:
0ffd37508c4a598298d94f0c2765114cd30ee97f7e739eb16bd9242aad138d518dc9c64be16e277975a79f96f2bc6dc18c84ee5d2056d1055f7125ee680a55b6364a66a6aa6f83743f5be558b08550586ba52bba59576bbebbf55ca06c12a43784dcbe37bef705e37ed30e73ecab4ed0d48569a9c6756d40f1f363005951d0a15b173673958b0fdc39a0b3aa3e21b71e9fa59f5552caaa656c90cea0920e15105f6f26899d4a6604b52f76f4e6ecd842a5c95aee0213b1abe48a6d36a2e34f57769cbcb963cc23765f253d998b8f21a9b7997cf42837d7b218ccab8d885a170bf589a6b41d9e6250c3a68c10429682dc1e65f7233aab8350a48fd13862734d8a
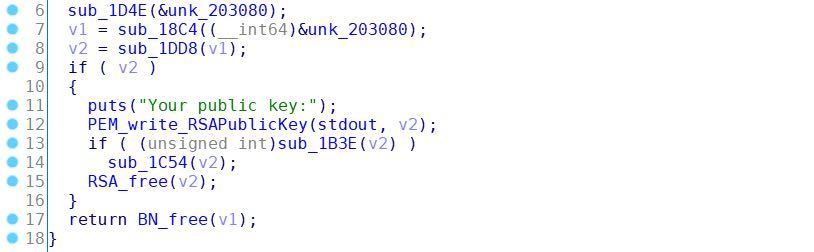
对程序进行逆向分析,定位到sub_1E25函数,程序首先通过sub_1D4E函数接收用户输入,然后通过sub_18C4处理我们输入的16进制字符串。
sub_1E25函数部分代码:
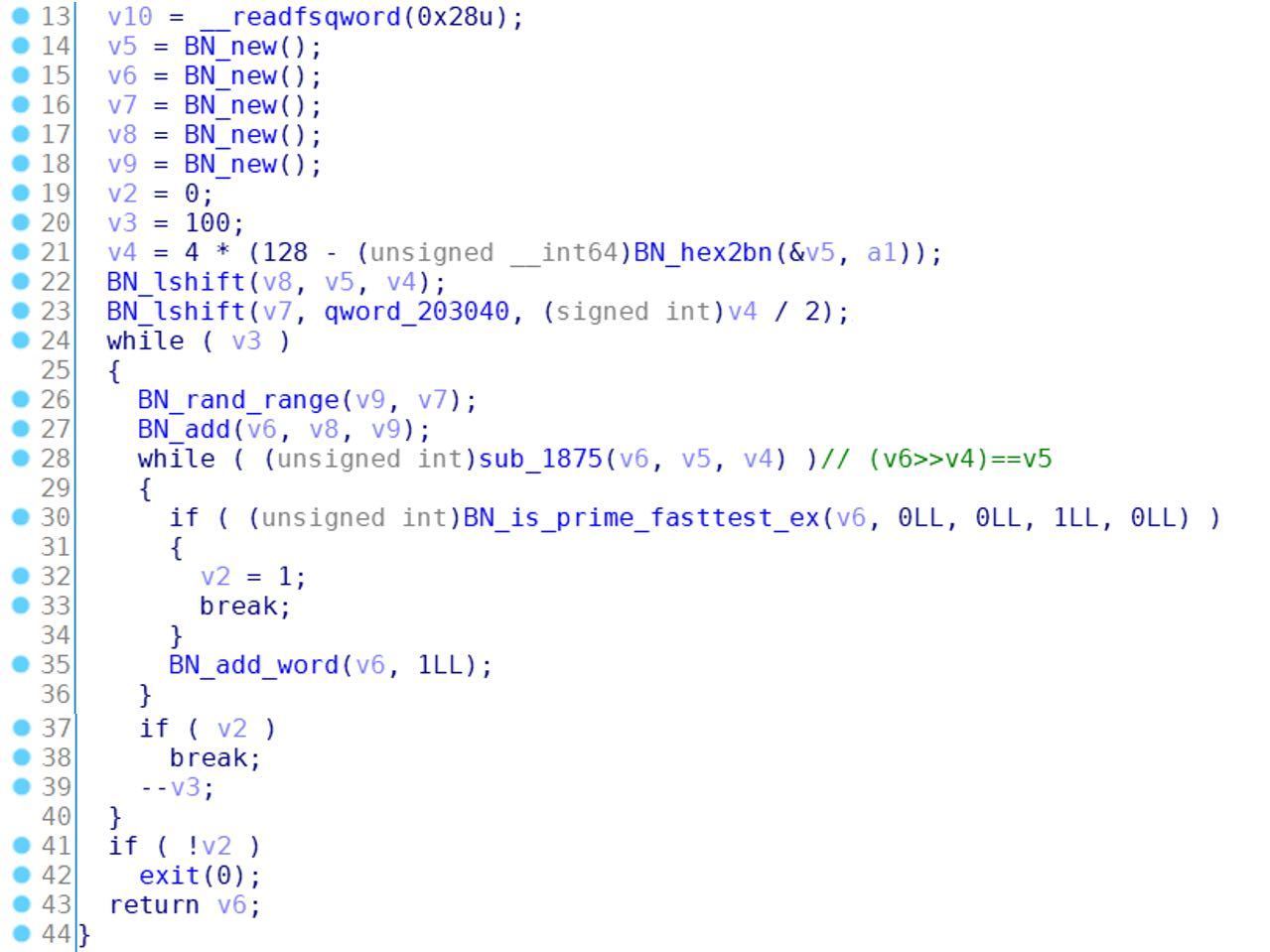
sub_18C4函数部分代码:
设sub_18C4函数的返回值为r,用户输入的16进制串的10进制整数形式为u,用户输入的16进制串的长度为l,x是区间[ 0, 2^(2 * (128 - l)) )上的一个随机数,则有:
接下来该函数会检查生成的r是否为素数,若为素数则返回r,否则将r值加1,继续判断是否为素数,若直到[r // 2^(4 * (128 - l))]不等于u时仍然不能找到一个素数r,则重新执行(1)式生产一个新的r并重复上述过程,直到找到一个素数r并返回该值。
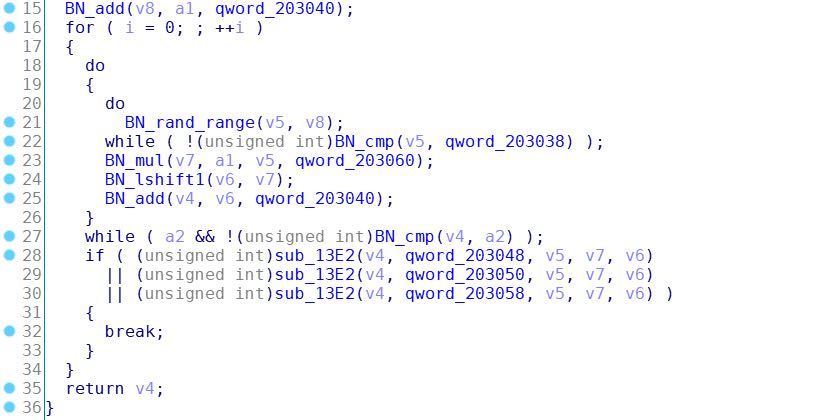
接下来sub_1DD8函数会根据r的值来生成公私钥对,sub_1DD8函数调用sub_14D8函数,根据r的值采用Pocklington定理生成素数p和q(p不等于q)。
sub_14D8函数部分代码:
即有:
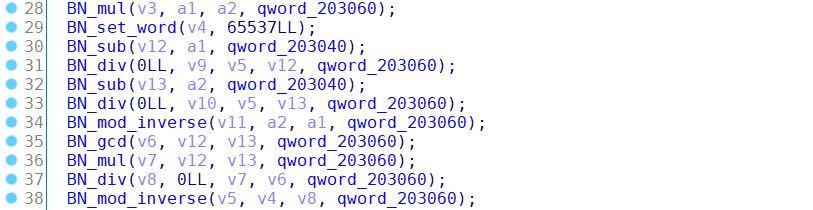
其中k_0和k_1是区间[0, r + 1)上的2个随机数,接下来sub_165E函数根据p和q来生成一对RSA公私钥,然后sub_1E25函数再通过PEM_write_RSAPublicKey函数以PEM格式打印公钥(e = 65537, N = p * q)。
sub_165E函数部分代码:
接下来程序调用sub_1B3E函数,该函数首先生成2个32比特的随机数x和y,然后使用前面生成的RSA公钥对字符串"What's the sum of " + str(x) + " and " + str(y) + "?"进行加密,并将加密后的密文以16进制形式打印给选手,此即为"Question"字符串后面的16进制串。接下来接收用户输入,如果用户输入的数等于x + y的值,则将FLAG经过前面生成的RSA公钥加密后的密文打印给选手,否则程序结束。
sub_1B3E函数部分代码:
因此为了拿到FLAG,我们需要通过分解N计算出程序使用的公钥对应的私钥,然后先使用该私钥解密"Question"字符串后面的密文,得到随机数x和y的值,再提交x + y的值,得到FLAG的密文,最后再使用该私钥对FLAG的密文进行解密,即可得到FLAG。
根据(2)式和(3)式,本题中N的表达式为:
在得到N的表达式后,首先说一下非预期解,非预期解无需用到任何Coppersmith相关攻击,对(4)式变形可得:
此时有:
观察(1)式中的x,x是区间[ 0, 2^(2 * (128 - l)) )上的一个随机数,当我们输入长度为最大长度120的16进制串时,x会落入[0, 2^16)这样一个小区间,此时我们可以穷举一个小区间,此时我们可以穷举x的值,对于穷举的每一个x,根据(1)式计算出其相应的r,然后根据(6)式是否成立来判断计算出的r是否正确,这样一来我们即可恢复出r的值。
恢复出r的值之后,对(5)式等式两边同除以2 * r,有:
此时有:
由于本题中p不等于q,根据(2)式和(3)式可知k_0不等于k_1,由于k_0和k_1都是区间[0, r + 1)上的随机数,因此一定有k_0 + k_1 < 2 * r,此时有:
联立(5)式和(9)式,即可求出k_0和k_1,从而成功分解N,继而解密密文拿到两个随机数的值,提交两个随机数的和拿到FLAG的密文,再次进行解密即可拿到FLAG。
接下来说一下预期解,本题原本是想考察Coppersmith相关攻击,观察(4)式,设:
则有:
设f(x) = 2 * r * x + 1, x in Zmod(N),然后我们仍然可以穷举r,此时我们可以通过Coppersmith相关攻击中计算计小整数解的方式来获取到x的值(也即k_0的值,k_1同理),POC如下(注意在SageMath下使用small_roots方法计算小整数解时要求多项式为首一多项式,因此我们需要将多项式形式做一个变形):
sage: P.<x> = PolynomialRing(Zmod(N))
....: f = x + inverse_mod(2 * r, N)
....: res = f.small_roots(X = r, beta = 0.4)
....: k_0 in res
....:
True
这样一来即可分解N,后面的步骤和前面相同,然后按照前面所说的步骤依次提交和计算即可拿到FLAG。
p.s.
根据(4)式中N的表达式,本题还可直接采用Coron attack(即双变量版本的Coppersmith攻击)来分解N,相关实现可见这里。
解题脚本
#!/usr/bin/env sage
import rsa
from gmpy2 import iroot
from pwn import *
from Crypto.Util.number import *
io = remote('coooppersmith.challenges.ooo', 5000)
#io = process("./service")
user_input = '000000000000000000000000000000000000000000000000000000000000111111111111111111111111111111111111111111111111111111111111'
io.sendline(user_input)
_ = io.recvline()
pkeydata = io.recvuntil("-----END RSA PUBLIC KEY-----\n")
_ = io.recvline()
sum_ct = int(io.recvline().strip(), 16)
pubkey = rsa.PublicKey.load_pkcs1(pkeydata)
N = pubkey.n
e = pubkey.e
for x in range(0, 2**16):
r = int(user_input, 16) * 2**32 + x
if (N - 1) % r == 0:
break
P.<x> = PolynomialRing(Zmod(N))
f = x + inverse_mod(2 * r, N)
res = f.small_roots(X = r, beta = 0.4)
k_0 = int(res[0])
p = 2 * r * k_0 + 1
q = N // p
d = inverse(e, (p - 1) * (q - 1))
sum_pt = pow(sum_ct, d, N)
tmp = long_to_bytes(sum_pt)
tmp = tmp[:-1].split(b"of ")[1].split(b" and ")
sum = int(tmp[0]) + int(tmp[1])
io.sendline(str(sum))
_ = io.recvline()
ct = int(io.recvline().strip(), 16)
pt = pow(ct, d, N)
FLAG = long_to_bytes(pt)
print(FLAG)
# OOO{Be_A_Flexible_Coppersmith}
notbefoooled
题目描述
What’s the trick to not be foooled?
notbefoooled.challenges.ooo 5000
143/500 pts, 30 solves
解题思路
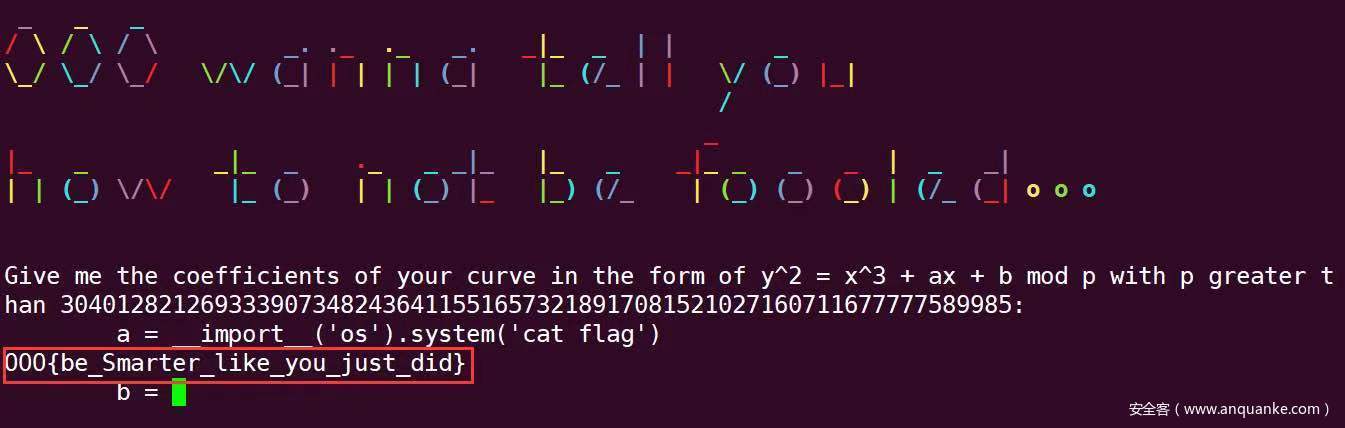
首先先说一下非预期解,本题本身预期是使用python3版本的SageMath来部署本题的Sage脚本,但是在部署时错误的使用了python2版本来部署,而本题在接受用户输入时直接使用了input函数,因此我们可以使用input函数的任意代码执行漏洞来直接拿到FLAG:
然后我们来看一下预期解,服务器首先要求选手提供一条椭圆曲线的a、b和p这3个参数的值,要求该曲线为anomalous曲线(即曲线的阶等于p)且p的值大于某一阈值,接下来服务器会随机选择该曲线的一个基点G并打印给选手,然后要求选手提交该曲线上的一个点G * k,随后服务器会用Smart’s attack对选手提供的曲线和点进行攻击,如果服务器成功计算出了k,则选手失败并中断连接,否则选手拿到FLAG。
那么接下来我们要分析的问题就是一条anomalous曲线在什么情况下会使得题目中给出的Smart’s attack的实现失效,查阅论文资料可以发现,Smart’s attack的思路是通过将F_p上的曲线提升到Q_p上来实现对ECDLP的化简计算的:
但是当提升后的Q_p上的曲线同F_p上的曲线同构(即出现canonical lift的情况)时,在(1)式(计算k的最终表达式)中的分子和分母均为0,此时我们无法再正确计算出k的值:
那么我们的问题就变成了如何生成一条anomalous曲线使得它到Q_p的trivial lift就是canonical lift,根据该篇论文我们可以看到,一个较为简单的方案就是直接选择d = 3, D = 3的情况(此时j不变量的值等于0),此时素数p应满足的表达式形如:
本题中的阈值预期p的值在220到225比特之间,因此我们可以在[2^113, 2^114]区间内穷举v的值(保证生成的p的值大于最大值),对于每一个v计算出一个p的值,同时我们计算出曲线的参数a和b的值为(参见3.2节):
由于j不变量的值等于0因此a的值直接为0,同时由于d % 8 == 3因此s的值为1,然后对于得到的每一组(p, a, b),生成椭圆曲线并检查曲线的阶是否等于素数p,若等于则向服务器提交该组(p, a, b),然后接收服务器返回的点G,生成一个随机数k并提交点G * k即可得到FLAG。
p.s.
实际上从论文中我们也可以看到,canonical lift出现的情况的概率约为1/p,我们本题之所以能够很快找到一种办法使得Smart’s attack失效,是因为本题中Smart’s attack的SageMath实现是有缺陷的(可以参见crypto.stackexchange中的这一问题),当我们实现Smart’s attack时,如果我们恰好落入了canonical lift的情况,只需要对lift随机化即可,即一个更为有效的Smart’s attack应该是将本题中的这行代码:
Eqp = EllipticCurve(Qp(p, 8), [ZZ(t) for t in E.a_invariants()])
修改为:
Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])
这样一来在很大程度上即可避免出现Smart’s attack攻击失败的这种情况。
解题脚本
#!/usr/bin/env sage
from pwn import *
'''
BITS = 113
def p_gen(BITS):
for i in range(2**BITS, 2**(BITS + 1)):
koeff = 1 + 3 * i * i
if koeff % 4 != 0:
continue
p = koeff // 4
if not is_prime(p):
continue
j_invar = 0
a = 0
b = (54 * 3 * pow(3 * 12**3, inverse_mod(2, p), p)) % p
E = EllipticCurve(GF(p), [a, b])
if p == E.order():
return (a, b, p)
'''
a = 0
b = 839808
p = 80879840001451919384001045261062739512883607574894458541090782884541
E = EllipticCurve(GF(p), [a, b])
io = remote("notbefoooled.challenges.ooo", 5000)
io.sendlineafter("a = ", str(a))
io.sendlineafter("b = ", str(b))
io.sendlineafter("p = ", str(p))
_ = io.recvuntil(b"generator: (")
tmp = io.recvline().strip().replace(b')', b'').split(b", ")
G = E(int(tmp[0]), int(tmp[1]))
k = randrange(1, p)
P = k * G
io.sendlineafter("x = ", str(P[0]))
io.sendlineafter("y = ", str(P[1]))
io.recv()
# OOO{be_Smarter_like_you_just_did}
ooo-flag-sharing
题目描述
Share flags safely with the latest OOO service!
ooo-flag-sharing.challenges.ooo 5000135/500 pts, 36 solves
解题思路
本题自定义了一个(5,100)门限的密钥共享协议,share的计算方式如下:
矩阵S中的100个元素代表100个share,矩阵X的第一个元素代表secret,其余4个元素代表区间[0, P]上的4个随机数(即计算时会将secret填充为一个5 X 1的矩阵),而矩阵M和P的值则分别来自prime.ooo和matrix.ooo这两个文件,其中prime.ooo文件存储的是一个256比特的安全素数,matrix.ooo文件存储的是一个100*5的随机矩阵,矩阵中每一个元素的值均为正整数且不超过1000。程序在首次启动时会对这两个文件进行初始化,由于程序每次会首先检查同目录下是否存在这两个文件,如果存在则直接读取已有文件而不再重新创建,因此本题中这两个文件中存储的内容对选手来讲恒定不变。
而已知任意5个share,我们即可根据下式恢复出矩阵X:
其中矩阵X的第一个元素即为secret,从而实现对secret的恢复。这里可以注意到,(1)式没有在模P下进行计算,而(2)式是在模P下进行计算的,这一漏洞为我们后面的攻击提供了可能,我们可以先记下这一漏洞。
接下来我们来看一下题目的流程,用户每次连接到服务器时,服务器会要求选手输入一个用户名,若不为程序设置的几个保留用户名,则会在同目录下创建一个shares/用户名目录,下次连接时如果还输入相同用户名则不再重复创建。接下来程序向选手提供了四个功能:
- 功能1
选手可以提供一个secret,然后程序将secret的16进制形式的md5哈希值的前6个字符作为secret_id,选手可以设置将其分享给num个人(num>=5),程序会根据secret的值生成num个share,然后将其随机置换,置换后的第一个share的值会保存在服务器上的该用户文件夹下的secret_id.1文件中,其余的share会打印给选手。
- 功能2
选手可以提供一个secret_id,再提供若干个share,服务器会使用该secret_id对应的一个share和选手提供的share来尝试恢复出secret,并将恢复出的内容打印给选手。
- 功能3
服务器将FLAG作为secret来生成5个share,然后将其随机置换,置换后的第一个share的值会保存在服务器上的该用户文件夹下的secret_id.1文件中,第二个share的值会保存在服务器上的该用户文件夹下的secret_id.2文件中,其余的3个share会打印给选手。同时程序随机生成一个3字节的字节串,将其16进制形式的字符串来作为secret_id。
- 功能4
选手可以提供一个secret_id,再提供若干个share,服务器会使用该secret_id对应的两个share和选手提供的share来尝试恢复出secret,若恢复出的内容以b"OOO{"开头,则会打印给选手恢复成功的提示。
接下来我们分析一下如何借助这些功能拿到FLAG,我们先来看一下预期解,首先我们执行一次功能3,拿到一个secret_id和3个share,设此时FLAG表示为:
其中s_a到s_e为关于FLAG的5个share,m_a到m_e为5 X 5矩阵M在模P下的逆矩阵中同s_a到s_e对应的5个值,假设这里s_a和s_b为服务器存储到secret_id.1和secret_id.2文件中的两个share,s_c、s_d和s_e为打印给选手的三个share,注意到在本题中,整数和字节串之间的转换是采用小端模式,此时功能4中检查字节串形式的FLAG是否以b"OOO{"开头即等价于检查整数形式的FLAG的低32位是否为:
01111011010011110100111101001111
那么假设选手将s_e的值修改为s_e + inverse(m_e, P) * (x << 32),此时根据(3)式,程序恢复出的结果将变为(FLAG + x << 32) % P,由于该操作是在模P下进行的,因此此时我们就可以将程序中的功能4看成一个ORACLE,然后在区间[0, P >> 32]上用二分搜索即可求出FLAG的值,即当(FLAG + x << 32) >= P的时候,此时恢复出的内容将不再以b"OOO{"开头;当(FLAG + x << 32) < P的时候,此时恢复出的内容仍以b"OOO{"开头,我们可以通过这种方法找到一个最小的x,使得(FLAG + x << 32) >= P成立,此时P - (x << 32)的值转换为字节串y后,b"OOO{" + y[4:]即为字节串形式的FLAG,从而我们恢复出了FLAG的内容。
那么要想按照这种利用ORACLE + 二分搜索的方法恢复出FLAG,首先我们需要先从服务器上泄漏出素数P的值,我们可以先利用两次功能1,提交两个其整数形式的值大于P的不同的字节串作为secret,设其对应的整数形式的值分别input_a和input_b,然后将得到的share分别提交到功能2,设恢复出的内容为secret_a和secret_b,则有:
将同余式转化为等式,有:
因此我们利用最大公约数恢复出P:
恢复出P以后,我们还需要恢复出m_e的值,我们可以令s_a到s_d的值均为0,令s_e的值为1,然后向功能2提交s_a到s_e这5个share,此时功能2恢复出来的即为m_e的值,但是由于s_a和s_b存入了文件,因此这里的下标a和b的值我们是未知的,但是鉴于a和b的取值范围为[1, 99](本题中split_secret返回的是shares[1:],因此下标值不会出现等于0的情况),因此我们可以遍历a和b的值,然后对于计算出的每一个m_e的值,我们将将s_e的值修改为s_e + inverse(m_e, P) * (1 << 32),然后向功能4提交s_c、s_d和s_e + inverse(m_e, P) * (1 << 32)进行测试,若功能4显示提示恢复成功,则可以认为此时的m_e恢复正确,此时所有需要的未知量我们都已确定,我们再使用上面提到的ORACLE + 二分搜索的方法恢复出FLAG即可。
接下来我们看一下非预期解,本题的非预期解可以直接在不使用功能4的情况下恢复出FLAG,首先我们需要恢复出矩阵M(即matrix.ooo文件中的内容),观察(1)式,假设我们使用多次(大于5次即可)功能1拿到若干组share,若我们将这些share组合成一个新的矩阵S,根据(1)式,对于新的矩阵S的转置中的每一个行向量,都可以由矩阵M的转置中的所有行向量的线性组合来表示,鉴于矩阵M中元素的值远远小于矩阵X和矩阵S中的元素的值,因此我们可以通过对矩阵S使用LLL算法进行格基规约,然后对规约后的矩阵的行向量之间的线性组合进行遍历,每得到一个所有元素的值均在区间[0, 1000)的行向量,即为矩阵M中的一个列向量,但是得到这些列向量之后我们无法确认这些列向量之间的排列顺序,因此可以尝试对其排列组合进行穷举,同时,由于本题中split_secret返回的是shares[1:],因此我们这种情况下无法准确恢复出矩阵M中的第一行,不过已经足够本题中恢复FLAG,鉴于X矩阵中的元素均小于P,我们可以收集足够数量的关于FLAG的share,然后通过使用LLL算法进行格基规约来解方程求出FLAG即可,相关实现可参考这里。
解题脚本
#!/usr/bin/env python3
from pwn import *
from math import gcd
from Crypto.Util.number import *
def fun_1(io, secret, num):
io.sendlineafter('Choice: ', '1')
io.sendlineafter('Enter secret to share: ', secret)
_ = io.recvuntil("Your secret's ID is: ")
secret_id = io.recvline().strip()
io.sendlineafter('Number of shares to make: ', str(num))
_ = io.recvuntil('Your shares are: ')
shares = eval(io.recvline().strip())
return secret_id, shares
def fun_2(io, secret_id, shares):
io.sendlineafter('Choice: ', '2')
io.sendlineafter("Enter the secret's ID: ", secret_id)
io.sendlineafter('Enter your shares of the secret: ', str(shares))
_ = io.recvuntil('Your secret is: ')
secret = io.recvline().strip()
secret = eval(secret)
return secret
def fun_3(io):
io.sendlineafter('Choice: ', '3')
io.recvuntil("Our secret's ID is: ")
secret_id = io.recvline().strip()
io.recvuntil("Your shares are: ")
shares = eval(io.recvline().strip())
return secret_id, shares
def fun_4(io, secret_id, shares):
io.sendlineafter('Choice: ', '4')
io.sendlineafter("Enter the secret's ID: ", secret_id)
io.sendlineafter("Enter your shares of the secret: ", str(shares))
res = io.recvline()
return res.startswith(b"Congrats!")
def recover_P(io):
input_a = b'~' * 40
input_b = b'~' * 41
secret_id, shares = fun_1(io, input_a, 5)
secret_a = fun_2(io, secret_id, shares)
secret_id, shares = fun_1(io, input_b, 5)
secret_b = fun_2(io, secret_id, shares)
kp = int.from_bytes(input_a, 'big') - int.from_bytes(secret_a, 'little')
gp = int.from_bytes(input_b, 'big') - int.from_bytes(secret_b, 'little')
P = gcd(kp, gp)
if not isPrime(P):
for i in range(2, 100, 2):
if isPrime(P // i):
P = P // i
break
return P
def recover_m_e(io, secret_id, shares, P):
known_idx = [share[0] for share in shares]
for a in range(1, 100):
for b in range(a + 1, 100):
if (a in known_idx) or (b in known_idx):
continue
m_e = int.from_bytes(fun_2(io, secret_id, [(a, 0), (b, 0), (known_idx[0], 0), (known_idx[1], 0), (known_idx[2], 1)]), 'little')
token = fun_4(io, secret_id, shares[:-1] + [(shares[2][0], (shares[2][1] + (1 << 32) * inverse(m_e, P)) % P)])
if token:
return m_e
def binary_search_x(io, secret_id, shares, P, m_e):
low = 0
high = P >> 32
while low <= high:
x = (low + high) // 2
token = fun_4(io, secret_id, shares[:-1] + [(shares[2][0], (shares[2][1] + (x << 32) * inverse(m_e, P)) % P)])
if token:
low = x + 1
else:
high = x - 1
return x
if __name__ == "__main__":
io = remote("ooo-flag-sharing.challenges.ooo", 5000)
io.sendlineafter("Username: ", "roadicing")
secret_id, shares = fun_3(io)
P = recover_P(io)
m_e = recover_m_e(io, secret_id, shares, P)
x = binary_search_x(io, secret_id, shares, P, m_e)
FLAG = b"OOO{" + (P - (x << 32)).to_bytes(32, 'little')[4:]
print(FLAG)
# OOO{ooo_c4nt_ke3p_secr3ts!}
参考资料
[1] https://www.tandfonline.com/doi/abs/10.1080/00207160212708?journalCode=gcom20
[2] https://github.com/ubuntor/coppersmith-algorithm
[3] https://wstein.org/edu/2010/414/projects/novotney.pdf
[4] https://link.springer.com/content/pdf/10.1007/s001459900052.pdf
[5] http://www.monnerat.info/publications/anomalous.pdf
[6] https://csrc.nist.gov/csrc/media/events/workshop-on-elliptic-curve-cryptography-standards/documents/papers/session1-miele-paper.pdf
[7] https://crypto.stackexchange.com/questions/70454/why-smarts-attack-doesnt-work-on-this-ecdlp
[8] https://gist.github.com/nomeaning777/8c8cc446fdf1e7a151ae30d72600c312