2021 ByteCTF-决赛 BabyHeaven 题解

360安全客 安全知识 45184 4

 

BabyHeaven

Status: Done ?
关键算法: 字典序算法
出处: 2021 ByteCTF-Final
原题链接: https://www.aliyundrive.com/s/vTGTA71VAGY
时间: December 11, 2021
考点: Shellcode, Windows API, 天堂之门, 算法优化
难度: 困难

分析

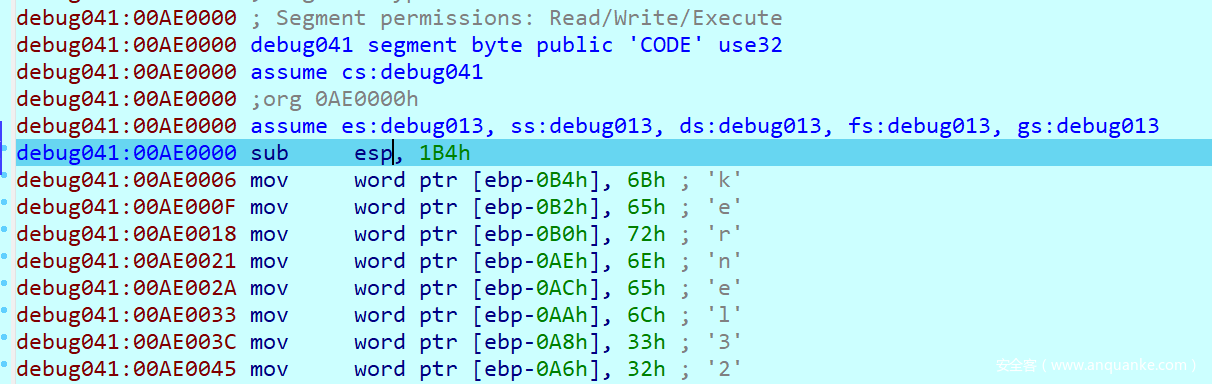
  1. 拿到题目，file 命令 check 一下，发现是一堆二进制数据，而非完整的可执行文件
  2. 试着往 IDA 里面一拖，发现所有数据都能被 IDA 反汇编出来，因此这其实就是一堆 shellcode

加载并运行 shellcode

  1. 自己写一个加载并运行 shellcode 的程序，争取能对它进行动调。由于 shellcode 是 32 位的，所以 loader 也要编译为 32 位的 
     #include <Windows.h>

 #include <fstream>
 #include <iostream>
 #include <string>

 using namespace std;

 typedef void (*func_ptr)();

 int main(int argc, char **argv) {
   if (argc < 2) {
     cout << "usage: shellcode_loader.exe [shellcode.bin]" << endl;
     exit(1);
   } else {
     printf("now trying to load %s", argv[0]);
     cout << endl;
   }
   ifstream infile(argv[1], ios::binary);
   infile.seekg(0, std::ifstream::end);
   int length = (int) infile.tellg();
   infile.seekg(0, std::ifstream::beg);
   auto shellcode = VirtualAlloc(nullptr, length, MEM_COMMIT, PAGE_EXECUTE_READWRITE);
   infile.read((char *) shellcode, length);
   auto ptr = (func_ptr) shellcode;
   ptr();
 }
  2. 发现程序会崩，对它进行动调，程序可以执行 shellcode 了
  3. 但是 shellcode 的头部并没有函数调用约定的特征，这会影响 IDA 的反汇编，所以对原本的 shellcode 进行 patch，加上 push ebp 之类的操作 
     with open("./BabyHeaven", "rb")as f:
   data = f.read()
   data = b'\x55\x8b\xec'+data
 with open("patched", "wb")as f:
   f.write(data)

分析 shellcode1

  1. 这时伪代码的可读性就增强了，可以从保存到栈里的字符串推断这是通过 GetProcAddress 等机制调用相关函数
  2. 发现这里有一部分逻辑调用了很多未知的函数
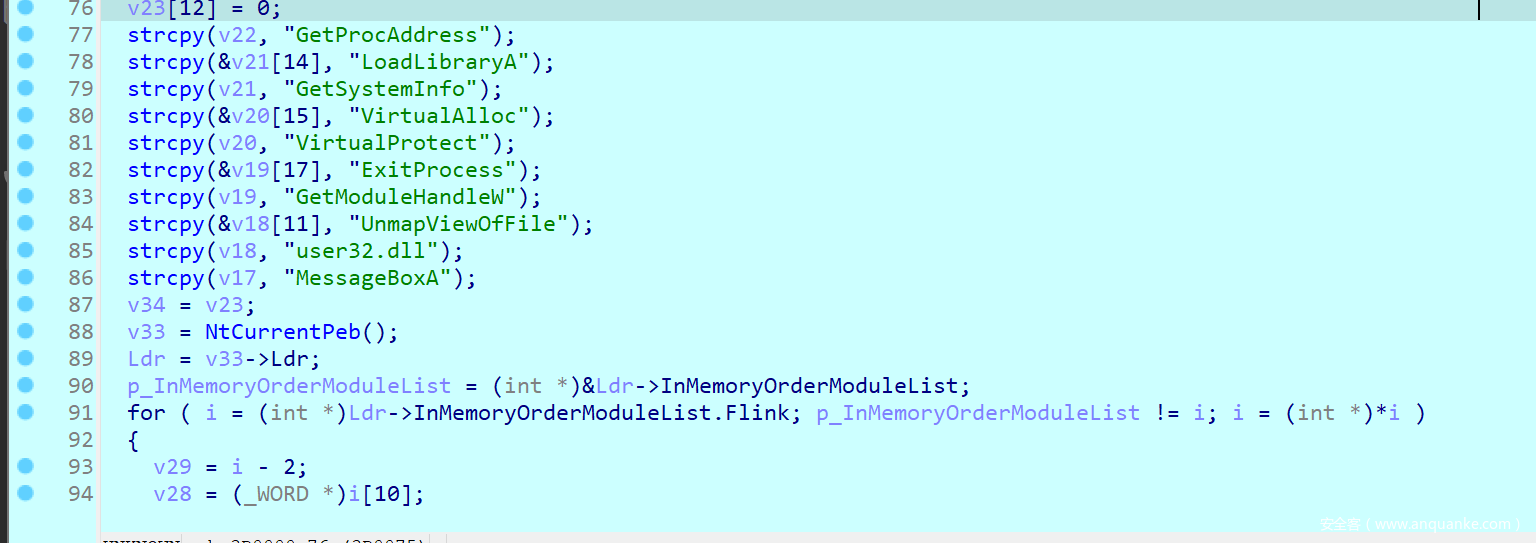
  3. 这时对 shellcode 动调，可以根据函数指针指向的地址对一些变量进行重命名，从而梳理程序逻辑如下。其实就是加载了一堆 Windows API 
     GetProcAddress_1 = GetProcAddress;
 LoadLibraryA = (int (__cdecl *)(char *))GetProcAddress(v71, &v21[14]);
 GetSystemInfo = (void (__cdecl *)(char *))GetProcAddress_1(v71, v21);
 VirtualAlloc = (int (__cdecl *)(_DWORD, int, int, int))GetProcAddress_1(v71, &v20[15]);
 VirtualProtect = (void (__cdecl *)(_BYTE *, int, int, char *))GetProcAddress_1(v71, v20);
 ExitProcess = GetProcAddress_1(v71, &v19[17]);
 GetModuleHandle = (int (__cdecl *)(_DWORD))GetProcAddress_1(v71, v19);
 UnmapViewOfFile = GetProcAddress_1(v71, &v18[11]);
 v64 = LoadLibraryA(v18);
 v14 = GetProcAddress_1(v64, v17);
 MessageBoxA = GetModuleHandle(0);
 GetSystemInfo(v12);
 v62 = v13;
 v61 = (_BYTE *)VirtualAlloc(0, v13, 4096, 4);
  4. 注意最后还调用了 VirtualAlloc ，说明这个 shellcode 还是个套娃，它又加载了第二段 shellcode
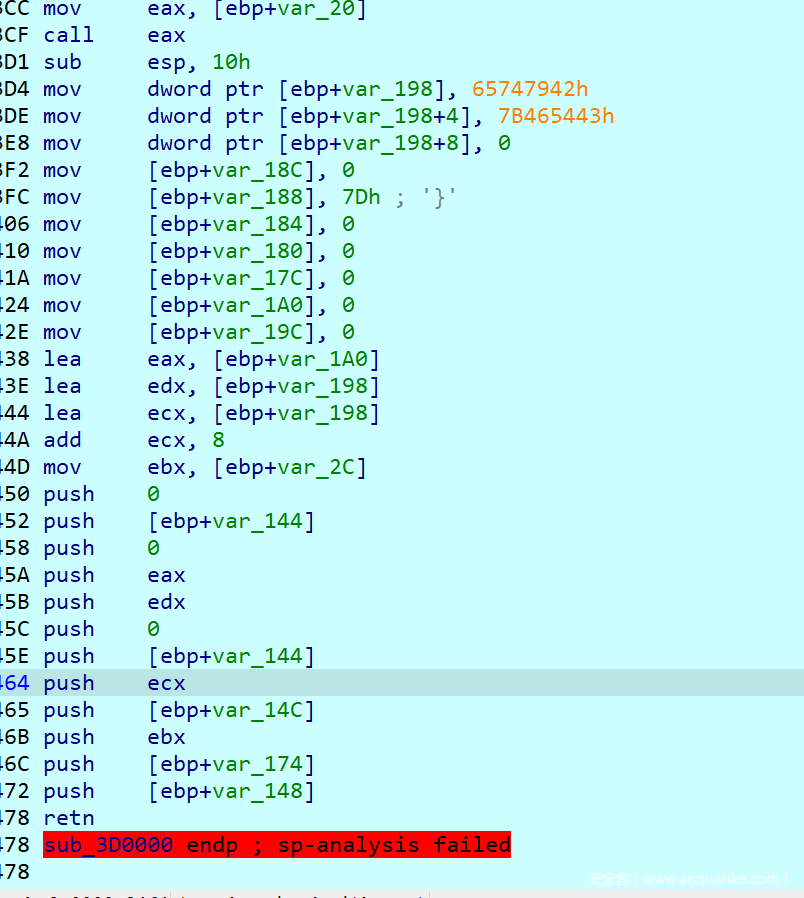
  5. 后面一大堆赋值命令就是在拿第二段 shellcode 填充 VirtualAlloc 申请的 buffer 
     *++v61 = 4;
 *++v61 = 36;
 *++v61 = 7;
 *++v61 = 72;
 *++v61 = -53;
 *++v61 = -62;
 *++v61 = 4;
 *++v61 = 0;
 VirtualProtect(++v61, v62, 64, v10);
 strcpy((char *)v4, "ByteCTF{");
 HIBYTE(v4[4]) = 0;
 v4[5] = 0;
 v5 = 0;
 v6 = 125;
 v7 = 0;
 v8 = 0;
 v9 = 0;
 __asm { retn }
  6. 最后的指令看伪代码看不懂了，这时需要对照汇编理解
  7. 这部分命令做了这几件事
    1. 填充为 ByteCTF{xxxxxxxx} ，x 是未填充的缓冲区
    2. 将指向这 char [8] 的指针压到栈里
    3. 构造 ROP 链，ROP 链所要实现的最终效果是 shellcode2(char*ptr) → MessageBoxA("ByteCTF{xxxxxxxx}")
  8. 由于 ROP 链里面并没有读取用户输入函数的身影，所以推测 shellcode2 实际上就是计算了 flag，因此可以判断这题目的实质是一个算法优化题

分析 shellcode2

  1. 由于此时已经具备了动调的能力，所以直接把 shellcode2 dump 出来即可，或者也可以把赋值的伪代码粘出来自己跑一遍
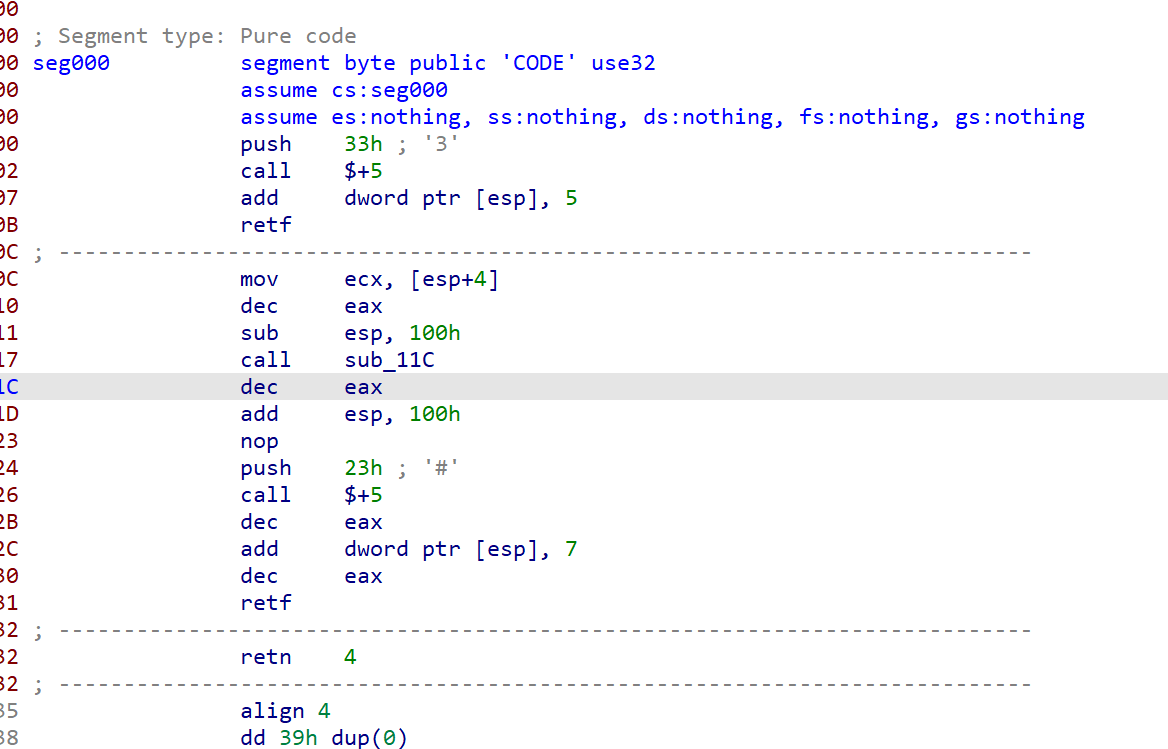
  2. 把 shellcode2 拖到 IDA 32位里面，上来就是这一段
  3. 起初以为只是花指令，所以就把他们无视了，直接来看后面的函数。但后面的函数明显有好多不正常的指令
  4. 然后看到 push 33h ，结合题目的名字，联想到了天堂之门技术。所以 shellcode2 上来的几条指令就是完成了 32 位到 64 位的切换，因此应该用 IDA 64位去分析后面的逻辑 
     void shellcode2_raw() {
   int length;  // [rsp+1C4h] [rbp+144h]
   int j;       // [rsp+1C8h] [rbp+148h]
   int i;       // [rsp+1CCh] [rbp+14Ch]
   int target[25] = {5, 18, 14, 23, 11, 17, 12, 4, 25, 24, 1, 20, 19, 15, 13, 10, 6, 21, 7, 22, 8, 3, 9, 2, 16};
   int buf[25] = {5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 1, 8, 11, 6, 13, 3};
   length = 25;
   uint64_t flag = 0;
   do {
     flag+=1;
     // 从结尾找递减序列
     for (i = length - 1; i > 0 && buf[i - 1] >= buf[i]; --i)
       ;
     if (i <= 0)
       break;
     // 将不在递减序列里的值引入递减序列中
     for (j = length - 1; j >= i && buf[i - 1] >= buf[j]; --j)
       ;
     // swap
     buf[i - 1] ^= buf[j];
     buf[j] ^= buf[i - 1];
     buf[i - 1] ^= buf[j];

     // 递减序列颠倒
     for (j = length - 1; i < j; --j) {
       buf[i] ^= buf[j];
       buf[j] ^= buf[i];
       buf[i++] ^= buf[j];
     }
     for (i = 0; i < length && buf[i] == target[i]; ++i) {
       ;
     }
   } while (i < length);
   cout << flag << endl;
 }
  5. 这里其实和逆向的关系不大了，考察的是阅读和理解算法的能力
  6. 每轮循环所执行的操作
    1. flag++
    2. 从结尾出发，找到一个递减序列
    3. 将不在递减序列里的值引入递减序列中
    4. 将找到的递减序列颠倒
    5. 判断此时被操作的序列是否与 target 相同，如果相同则 break 并输出 flag（源程序里是调用 MessageBoxA 输出）
  7. 因此，题意的本质就是求从初始的 buf 到 最终的 target 要经历多少轮操作
  8. 运行一下，发现是非常耗时的，说明里面有大量的无用功
  9. 通过观察每一轮中被操作序列的变化，可以发现无用功来自于这个颠倒的操作。每次当长度为 n 的序列被颠倒，就要有 n! 轮操作去逆转这个操作
  10. 因此，从 buf 到 target 的排序过程可以拆解为三部分
    1. 排序的次数
    2. 逆转反序操作的次数
    3. 最后一轮的逆转操作中，从开始到 target 所要经历的次数
  11. 先看一下，只执行排序过程时，序列的变化（把逆序操作部分的代码删除，并添加打印的代码即可） 
    5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 1, 8, 11, 13, 6, 3, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 1, 8, 13, 11, 6, 3, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 1, 11, 13, 8, 6, 3, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 1, 13, 11, 8, 6, 3, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 3, 13, 11, 8, 6, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 6, 13, 11, 8, 3, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 8, 13, 11, 6, 3, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 11, 13, 8, 6, 3, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 13, 11, 8, 6, 3, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 8, 13, 11, 7, 6, 3, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 11, 13, 8, 7, 6, 3, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 13, 11, 8, 7, 6, 3, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 3, 17, 13, 11, 8, 7, 6, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 6, 17, 13, 11, 8, 7, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 7, 17, 13, 11, 8, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 8, 17, 13, 11, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 11, 17, 13, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 13, 17, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 17, 13, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 17, 16, 13, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 13, 17, 16, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 16, 17, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 17, 16, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 22, 25, 24, 19, 17, 16, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 24, 25, 22, 19, 17, 16, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 25, 24, 22, 19, 17, 16, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 22, 25, 24, 20, 19, 17, 16, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 24, 25, 22, 20, 19, 17, 16, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 10, 25, 24, 22, 20, 19, 17, 16, 13, 12, 11, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 11, 25, 24, 22, 20, 19, 17, 16, 13, 12, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 12, 25, 24, 22, 20, 19, 17, 16, 13, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 13, 25, 24, 22, 20, 19, 17, 16, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 16, 25, 24, 22, 20, 19, 17, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 17, 25, 24, 22, 20, 19, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 19, 25, 24, 22, 20, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 20, 25, 24, 22, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 22, 25, 24, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 24, 25, 22, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 21, 25, 24, 22, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 22, 25, 24, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 24, 25, 22, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 4, 25, 24, 22, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 6, 25, 24, 22, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 7, 25, 24, 22, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 8, 25, 24, 22, 21, 20, 19, 17, 16, 13, 12, 11, 10, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 10, 25, 24, 22, 21, 20, 19, 17, 16, 13, 12, 11, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 11, 25, 24, 22, 21, 20, 19, 17, 16, 13, 12, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 12, 25, 24, 22, 21, 20, 19, 17, 16, 13, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 13, 25, 24, 22, 21, 20, 19, 17, 16, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 16, 25, 24, 22, 21, 20, 19, 17, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 17, 25, 24, 22, 21, 20, 19, 16, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 19, 25, 24, 22, 21, 20, 17, 16, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 20, 25, 24, 22, 21, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 21, 25, 24, 22, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 22, 25, 24, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 24, 25, 22, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 15, 25, 24, 22, 21, 20, 19, 17, 16, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 16, 25, 24, 22, 21, 20, 19, 17, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 17, 25, 24, 22, 21, 20, 19, 16, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 19, 25, 24, 22, 21, 20, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 20, 25, 24, 22, 21, 19, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 21, 25, 24, 22, 20, 19, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 22, 25, 24, 21, 20, 19, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 24, 25, 22, 21, 20, 19, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 9, 25, 24, 22, 21, 20, 19, 17, 16, 15, 13, 12, 11, 10, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 10, 25, 24, 22, 21, 20, 19, 17, 16, 15, 13, 12, 11, 9, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 11, 25, 24, 22, 21, 20, 19, 17, 16, 15, 13, 12, 10, 9, 8, 7, 6, 4, 3, 2, 1, 
5, 18, 14, 23, 12, 25, 24, 22, 21, 20, 19, 17, 16, 15, 13, 11, 10, 9, 8, 7, 6, 4, 3, 2, 1,
  12. 可以发现，在开始 5, 18, 14, 23, 11 为首的迭代前，整个序列会先排列到 5, 18, 14, 23, 10, 25, 24, 22, 21, 20, 19, 17, 16, 15, 13, 12, 11, 9, 8, 7, 6, 4, 3, 2, 1 的状态
  13. 先求得从初始状态到这个序列需要的轮数为 3503378891785895936 
    #include <cstdint>
#include <iostream>

using namespace std;

int main() {
  int length;  // [rsp+1C4h] [rbp+144h]
  int j;       // [rsp+1C8h] [rbp+148h]
  int i;       // [rsp+1CCh] [rbp+14Ch]
  int target[25] = {5, 18, 14, 23, 10, 25, 24, 22, 21, 20, 19, 17, 16, 15, 13, 12, 11, 9, 8, 7, 6, 4, 3, 2, 1};
  int buf[25] = {5, 18, 14, 23, 9, 15, 4, 21, 10, 20, 19, 25, 24, 22, 12, 16, 2, 17, 7, 1, 8, 11, 6, 13, 3};
  uint64_t array[26];
  uint64_t mul = 1;
  for (i = 1; i <= 25; i++) {
    mul *= i;
    array[i] = mul - 1;
  }
  //
  length = 25;
  uint64_t flag = 0;
  int inc;
  do {
    flag += 1;
    // 从结尾找递减序列
    for (i = length - 1; i > 0 && buf[i - 1] >= buf[i]; --i)
      ;
    if (i <= 0)
      break;
    // 将不在递减序列里的值引入递减序列中
    for (j = length - 1; j >= i && buf[i - 1] >= buf[j]; --j)
      ;
    // 把找到的递减序列逆序
    buf[i - 1] ^= buf[j];
    buf[j] ^= buf[i - 1];
    buf[i - 1] ^= buf[j];
    flag += array[length - i];
    for (i = 0; i < length; i++) {
      printf("%d, ", buf[i]);
    }
    cout << endl;
    for (i = 0; i < length && buf[i] == target[i]; ++i) {
      ;
    }

  } while (i < length);
  cout << flag << endl;
}
  14. 最后一个难点，就是如何确定从 5, 18, 14, 23, 10, 25, 24, 22, 21, 20, 19, 17, 16, 15, 13, 12, 11, 9, 8, 7, 6, 4, 3, 2, 1 到 target 需要的部署。这时就需要观察一下循环过程中，序列的变化
  15. 可以发现，在去做无用功的过程中，实质上就是对尾部长度为 n 的序列做一个全排列，而且这个排列是有序的
  16. 因此，只要求得 17, 12, 4, 25, 24, 1, 20, 19, 15, 13, 10, 6, 21, 7, 22, 8, 3, 9, 2, 16 （target 的后 20 个数字）在排列过程中的字典序即可
  17. 在网上查到了这种算法，自己推其实也能推出来，原理不复杂康托展开

    康托展开 – 维基百科，自由的百科全书

  18. 最终与前面求到的 3503378891785895936 相加即可。注意字典序是从 0 开始的，最终要还要再加 1 
    def cantor(nums: List[int]):
  res = 0
  for i in range(len(nums)):
    subset = list(sorted(nums[i+1:]))
    A = 0
    for j in subset:
      if nums[i] > j:
        A += 1
    for j in range(len(subset)):
      A *= (j+1)

    res += A
  return res

suffix = [17, 12, 4, 25, 24, 1, 20, 19,
          15, 13, 10, 6, 21, 7, 22, 8, 3, 9, 2, 16]
c = cantor(suffix) & 0xffffffffffffffff
flag = (3503378891785895936 + c+1) & 0xffffffffffffffff
print(b"ByteCTF{"+flag.to_bytes(8, "little")+b"}")
  19. 得到 flag ByteCTF{Qw021zbG}
（完）