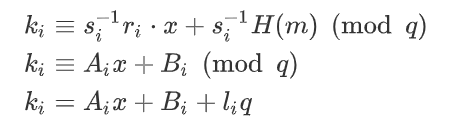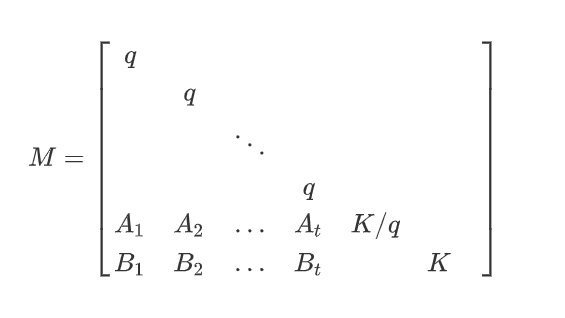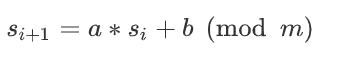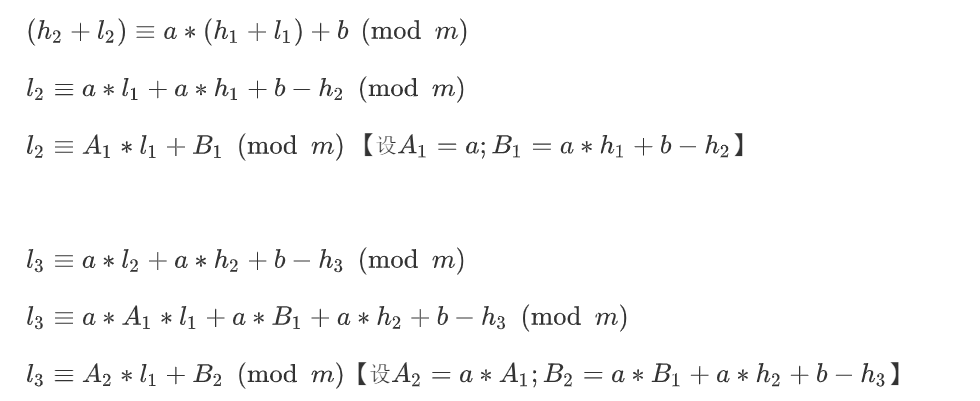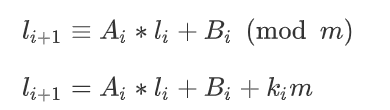前言
格密码是一类备受关注的抗量子计算攻击的公钥密码体制。而格理论也使许多现代公钥密码RSA、DSA等体系受到影响。这篇文章主要从两道CTF题目来学习格密码中的HNP(Hidden number problem)。
Lattice
首先谈谈个人对Lattice的理解叭。个人觉得,Latiice就是由若干线性无关的向量组成的一个向量空间,在这个空间中,向量彼此之间可以进行相应的加、减运算。向量也可以乘以某个系数,但这个系数仅限于整数,因而形成了布满整个空间的格点。在格中的计算问题主要包括两种,即SVP(the Shortest Vector Problem of lattice)和CVP(the Closest Vector Problem),然后个人认为,CVP可以给Latiice加上一个维度后变成SVP,继而可以用LLL算法来进行规约从而找到最短向量。
XCTF2020-高校战役-NHP
题目信息
题目用的是DSA公钥密码签名系统。
题目提供签名函数:用户以用户名注册,服务端返回签名,并提供所用临时密钥的bit长度
我们需要以admin的身份登陆来获取flag,但是服务端不会给admin签名
解题流程
根据题目流程,显然,我们要利用临时密钥的bit长度来获取私钥,从而获得admin的签名
其中,我们知道的信息全局公钥p, q, g,服务端公钥y , 每轮签名使用的r, s, 以及我们可控的H(x),x即为用户名,Hash函数这里用的是sha256
step1-公式转化
由DSA签名中各参数的关系
可得每轮临时密钥与签名、明文的关系
其中ki就是每次使用的临时密钥
化简后的式子中的Ai,Bi均可由已知信息计算
step2-构造Lattice
对于上式中的ki,我们仅仅知道它的bit_ength,bit_ength泄露了什么信息呢?
当我们知道一个数的bit_ength时,我们能确定这个数的大小范围,
比如一个数的bit_ength是500时,我们能确定这个数大小落在(2^499)-1与(2^500)-1 之间
所以我们知道这个数的MSB位为2^499
这等价于,我们知道了临时密钥的一个大概的值,我们设其为K
然后我们构造Lattice
然后这里就会存在一个向量
使得
其中向量v中的x即为我们的私钥,
step3-LLL
解决格密码的问题LLL算法的运用总是必不可少的,可是这里我们该如何利用LLL算法去找到向量vk呢?
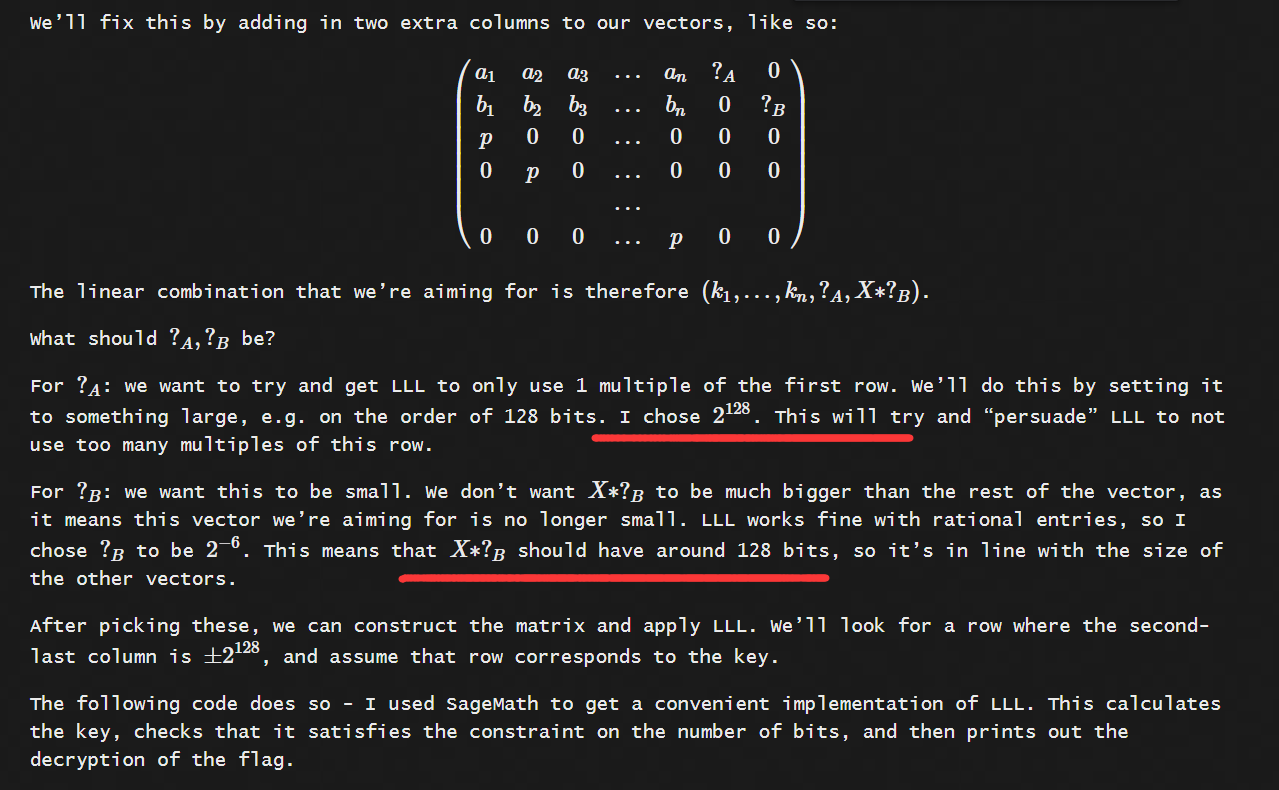
如果我们的vk的长度在格中很小,我们利用LLL就很可能将其找出。所以,我们需要与服务端交互,然后收集当ki的bit_length比较小的情况时的相关数据。比如:我们知道q的bit_length为128,那我们可以找bit_legnth为122的ki,然后我们还需要一定的数据量,这样能提高利用LLL算法找到这个短向量的概率,并且,上述格中K/q, K的构造也是为了让vk中的每一项的长度都差不多,这样也有利于找到vk,参考这一篇文章中的
参考祥哥博客的这篇出题文章,另外感谢祥哥的解惑。
NPUCTF2020-babyLCG
题目附件可以在BUUOJ下载
题目流程
- 初始化一个LCG加密类,用到随机参数a, b, m, seed,其中a, b, m,均在附件给出
- 生成20个128位的随机数,但是只给出每个数的高64位
- 再生成三个随机数,用AES加密加密flag,key由前两个随机数组成,分别取第一个随机数和第二个随机数的高64位拼起来,iv由第三个随机数组成
解题思路
从题目流程来看,我们目的只有一个,恢复seed。
step1-公式转化
LCG生成随机数的公式为:
但是这一题,我们只知道s1 到s20的高64位,所以我们将si分为h、l高低位两部分,其中hi已知。所以有
这里,我们通过公式的变形,可以将原来式子
中s{i+1}和s{i}的关系转变为l{i+1}和l{i}的关系。当然,原系数a、b的意义也发生了对应转变。
这里给出生成新A 和B 的脚本
b=153582801876235638173762045261195852087
a=107763262682494809191803026213015101802
m=226649634126248141841388712969771891297
h = [0,7800489346663478448,11267068470666042741,5820429484185778982,6151953690371151688,548598048162918265,1586400863715808041,7464677042285115264,4702115170280353188,5123967912274624410,8517471683845309964,2106353633794059980,11042210261466318284,4280340333946566776,6859855443227901284,3149000387344084971,7055653494757088867,5378774397517873605,8265548624197463024,2898083382910841577,4927088585601943730]
for i in range(len(h)):
h[i] <<= 64
A = [1]
B = [0]
for i in range(1, len(h)-1):
A.append(a*A[i-1] % m)
B.append((a*B[i-1]+a*h[i]+b-h[i+1]) % m)
print(A[1:])
print(B[1:])
step2-构造Lattice
现在我们二十条与 l 相关的方程组了。即
且对于 l 我们真的一无所知么?我们其实知道 l 是小于2^64的,即 l 最大为64bit。这样与前面一道题就很类似了。
其中l1即为s1的低位,拼上其高位,在利用a, b, m就能会恢复seed了
step3-LLL
这里我们的vl向量每一位都只有约64bit,显然,它是整个格中比较短的向量了,且我们一共有19组数据,那么直接对这个Lattice M运用LLL算法就可以找到vl了。(格中参数2^{64}的选取道理与上面一致)
完整exp:
'''
#sage
b=153582801876235638173762045261195852087
a=107763262682494809191803026213015101802
m=226649634126248141841388712969771891297
h = [0,7800489346663478448,11267068470666042741,5820429484185778982,6151953690371151688,548598048162918265,1586400863715808041,7464677042285115264,4702115170280353188,5123967912274624410,8517471683845309964,2106353633794059980,11042210261466318284,4280340333946566776,6859855443227901284,3149000387344084971,7055653494757088867,5378774397517873605,8265548624197463024,2898083382910841577,4927088585601943730]
for i in range(len(h)):
h[i] <<= 64
A = [1]
B = [0]
for i in range(1, len(h)-1):
A.append(a*A[i-1] % m)
B.append((a*B[i-1]+a*h[i]+b-h[i+1]) % m)
A = A[1:]
B = B[1:]
M = matrix(ZZ, 21, 21)
for i in range(19):
M[i, i] = m
M[19, i] = A[i]
M[20, i] = B[i]
M[i, 19] = M[i, 20] = 0
M[19, 19] = 1
M[20, 20] = 2^64
M[19, 20]= 0
#print(B)
vl = M.LLL()[0]
l1 = vl[-2]
h1 = h[1]
s1 = l1+h1
#s1 = a*seed+b %m
seed = ((s1 - b)*inverse_mod(a,m))%m
print(seed)
'''
#python
from Crypto.Util.number import *
from Crypto.Cipher import AES
class LCG:
def __init__(self, bit_length):
b = 153582801876235638173762045261195852087
a = 107763262682494809191803026213015101802
m = 226649634126248141841388712969771891297
seed = 73991202721494681711496408225724067994
self._key = {'a':a, 'b':b, 'm':m}
self._state = seed
def next(self):
self._state = (self._key['a'] * self._state + self._key['b']) % self._key['m']
return self._state
def export_key(self):
return self._key
def gen_lcg():
rand_iter = LCG(128)
key = rand_iter.export_key()
f = open("key", "w")
f.write(str(key))
return rand_iter
def leak_data(rand_iter):
f = open("old", "w")
for i in range(20):
f.write(str(rand_iter.next() >> 64) + "n")
return rand_iter
def encrypt(rand_iter):
f = open("ct", "wb")
key = rand_iter.next() >> 64
key = (key << 64) + (rand_iter.next() >> 64)
key = long_to_bytes(key).ljust(16, b'x00')
iv = long_to_bytes(rand_iter.next()).ljust(16, b'x00')
cipher = AES.new(key, AES.MODE_CBC, iv)
pt = flag + (16 - len(flag) % 16) * chr(16 - len(flag) % 16)
ct = cipher.encrypt(pt.encode())
f.write(ct)
def decrypt(rand_iter):
with open("ct", "rb") as f:
flag = f.read()
key = rand_iter.next() >> 64
key = (key << 64) + (rand_iter.next() >> 64)
key = long_to_bytes(key).ljust(16, b'x00')
iv = long_to_bytes(rand_iter.next()).ljust(16, b'x00')
cipher = AES.new(key, AES.MODE_CBC, iv)
ct = cipher.decrypt(flag)
print(ct)
def main():
rand_iter = gen_lcg()
rand_iter = leak_data(rand_iter)
decrypt(rand_iter)
if __name__ == "__main__":
main()
总结
从这两题我们可以发现,解决HNP问题,一般我们需要多组数据,然后每一组就像方程组中的每一条方程,我们根据这些方程组构造一个Lattice,也可以认为是一个矩阵,就好像在用矩阵解决线代中的 XA=B 的问题,这个B中的每一项是我们获得的MSB这样子的比较模糊的信息(上面两题我们拿到的都是未知量的bit_length,也相当于MSB)。然后这个B向量的长度(范式)需要相对与格中其他向量要短,然后我们就可以利用LLL算法找到这个B,进而根据我们的构造,确定X向量中我们需要的一个特定的值。也就是方程组的解。
需要再次说明的是,这个矩阵所代表的方程组并非像真正的线代中的XA=B问题中的方程组——是多元的。我们这里的方程组是一元的。如果正常解方程的话,之所以这么多条方程都算不出解,就是因为我们得到信息是模糊的,并非是准确的。故我们需要用到格理论,和一个超好用的LLL算法。