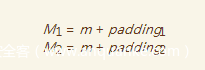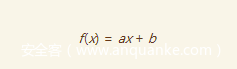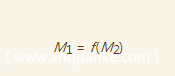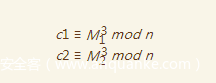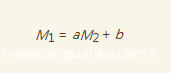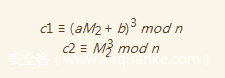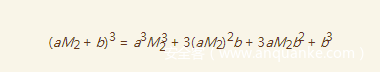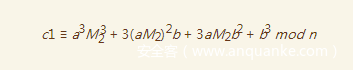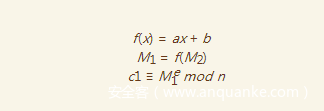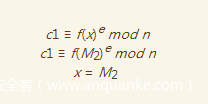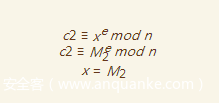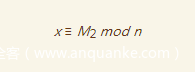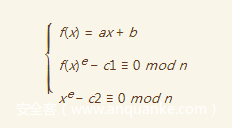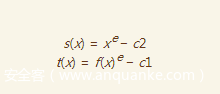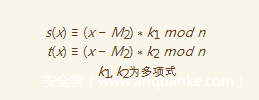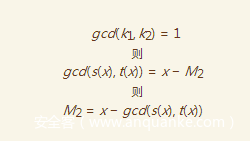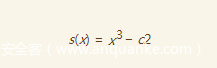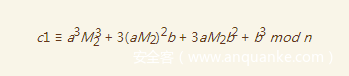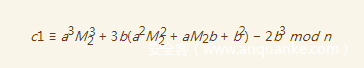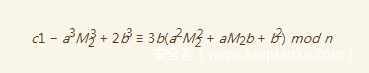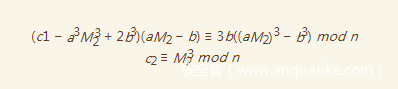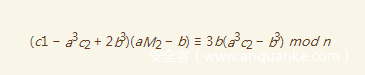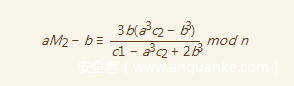前言
近日在复盘一些Crypto的题目,做到了N1CTF的一道rsapadding,进行了一些拓展,于是进行了一些分析记录,有了这篇文章
题目分析
题目已开源在
https://github.com/Nu1LCTF/n1ctf-2018/tree/master/source/crypto/rsapadding
主要代码为
m = '*****************'
n = 21727106551797231400330796721401157037131178503238742210927927256416073956351568958100038047053002307191569558524956627892618119799679572039939819410371609015002302388267502253326720505214690802942662248282638776986759094777991439524946955458393011802700815763494042802326575866088840712980094975335414387283865492939790773300256234946983831571957038601270911425008907130353723909371646714722730577923843205527739734035515152341673364211058969041089741946974118237091455770042750971424415176552479618605177552145594339271192853653120859740022742221562438237923294609436512995857399568803043924319953346241964071252941
e = 3
welcom()
if cmd():
f = open("/root/crypto/file.py")
print(f.read())
return
mm = bytes_to_long(m)
assert pow(mm, e) != pow(mm, e, n)
sys.stdout.write("Please give me a padding: ")
padding = input().strip()
padding = int(sha256(padding.encode()).hexdigest(),16)
c = pow(mm+padding, e, n)
print("Your Ciphertext is: %s"%c)
意思很简单
1.pow(mm, e) != pow(mm, e, n)
2.输入一个值
3.将输入的值sha256,记做padding
4.利用rsa加密m+padding
值得注意的是,e=3,padding可控
那么我们拥有的条件只有
n,e,c,padding
所以这里的攻击肯定是要从可控的padding入手了
初步推导
我们可以随便构造一对已知padding的密文,得到
此时,我们可以设
利用这两个式子,我们可以得到如下线性关系
即方程形式为
其中
即
我们有
我们知道
那么将其带入得到
我们将c1展开得到
我们将这个式子带入得到
于是便一筹莫展
可求证明
上述的推导我们漏了一个非常重要的信息
那么不难发现
同理,我们还可以构造方程
如此一来,我们可以得到
是下列方程组的一个解
那么一定可以有
可以被写成
如此一来,只要
我们由e=3可以得知
只有唯一解,所以k1和k2必互素,所以这里是M2一定是可求的
Related Message Attack
前面做了这么多证明铺垫,最后当然要祭出大招,即求解方法
这里的攻击是有方法名称的,即Related Message Attack
在e=3的情况下,我们可以利用rsa padding得到明文
根据之前第一步的推导,我们得到了
我们将式子变形为
移项得到
根据立方差公式,我们又有
联立
我们将式子1左右同乘aM2-b,将式子2左右同乘3b
然后即可得到如下式子
我们再把c2带入得到
则最后可以有
即可求得M2
而我们知道
所以最后有
注意,这里的分式不是除法,是逆元
payload
既然推导出了公式,写脚本即可
def getM2(a,b,c1,c2,n):
a3 = pow(a,3,n)
b3 = pow(b,3,n)
first = c1-a3*c2+2*b3
first = first % n
second = 3*b*(a3*c2-b3)
second = second % n
third = second*gmpy2.invert(first,n)
third = third % n
fourth = (third+b)*gmpy2.invert(a,n)
return fourth % n
m = getM2(a,b,c1,c2,n)-padding2
print libnum.n2s(m)
Coppersmith’s short-pad attack
上述情况是e=3时候,我们可以根据
推导出m
那么当e不是3的时候怎么办呢?
这里稍作拓展,我们可以用Coppersmith’s short-pad attack,即padding过短引起的攻击
脚本如下
https://github.com/ValarDragon/CTF-Crypto/blob/master/RSA/FranklinReiter.sage
后记
根据这一次学习,不难发现在存在padding的情况下,rsa也存在各种风险:
1.若e=3,则可以利用Related Message Attack
2.若e不为3,但padding过短,则可以利用Coppersmith’s short-pad attack