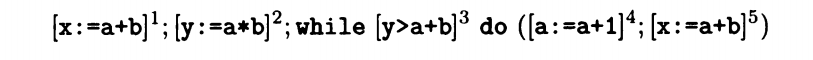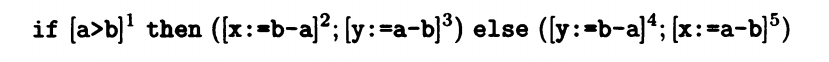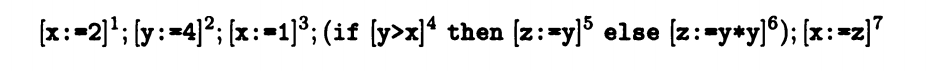前言
程序分析理论第四篇 关于数据流分析的部分理论证明。这一部分只包含笔者粗浅理解的部分,如有不对之处,欢迎指点。也欢迎各位交流
理论证明 Theory
我们十分熟悉数学归纳法,数学归纳法是对一组无穷项的数列进行数据归纳的一种方式。结构归纳法与其类似,是对任意大小的结构进行归纳的一种方式。即:提出一个针对最小结构单元以及任意子结构都成立的命题
举一个例子
我们以二分查找算法为例:
存在一组有序数列3,4,5,7,2,1,6,8
第一次查找将数列分成两部分:3,4,5,7和2,1,6,8
第二次查找再细分:3,4 5,7 2,1 6,8
第三次查找: 3 4 5 7 2 1 6 8
每一次都将整体分成两个部分,直到最后只有一个最小单元。每一个子结构都满足最初结构的属性。这就是结构归纳法
结构上的操作语义 Structural Operational Semantics
而结构归纳法在程序分析中的应用就是将代码块分解成最小单元代码进行描述。在对结构描述之前,先对数理结构进行简单描述
数据类型
整型描述: A[x]σ = σ(x) 对于整数型操作语句 变量 x 为 σ(x)
A[n]σ = N[n] 对于整数型操作语句 值为N[n]
A[a1 opa a2]σ = A[a1]σ opa A[a2]σ 对于AExp的操作描述,将各元素描述后进行操作。
布尔型描述:B[not b]σ = ┐ B[b] σ 对于布尔型操作语句 not 用┐描述
B[b1 opb b2]σ = B[b1]σ opb B[b2]σ 对于大的布尔结构进行细化描述
B[a1 opb a2]σ = A[a1]σ opb A[a2]σ 对于最小的结构先对元素各自描述再对操作描述
之后对结构进行描述
对于结构的描述可以用<S,σ>表示,而对于一个结构,他可能是复杂结构或者是简单结构。也就是说,<S,σ> 的结果可能是一个确定的值,也可能是仍需要执行的S 以及已经得到的中间结果σ。
用符号表示:<S,σ> -> σ’ and <S,σ> -> <S’,σ’>
此时,我们可以对所有不同类型的语句进行描述:
对于赋值语句 x=a 可以描述成 \<[x:=a]^l , σ> -> σ[x -> A[a]σ ]
代码块 S1, S2 描述成 <S1,σ> —> <S1′,σ’> | <S1;S2,σ> —> <S1′;S2,σ’> (S1为复杂语句,执行一步后,得到σ‘ ,剩余S1部分和S2 当作新的整体)
也可以能是<S1,σ> —> σ’ | <S1;S2,σ> —> <S2,σ’> (S1是简单语句,一步执行可以完成所有操作 )
面对判断语句 我们描述为 <if [b]^l then S1 else S2 , σ> —> <S1,σ> 当真时
<if [b]^l then S1 else S2 , σ> —> <S2,σ> 当假时
面对while语句 我们描述为 \<while [b]^l do S, σ \> —> <(S;while [b]^l do S ),σ> 当真时
<while [b]^l do S ,σ > —> σ 当假时
我们来对下面一个例子进行尝试
< [x:=5]^1 ; [y:=1]^2 ; while [x>1]^3 do ([y:=x*y]^4 ; [x:=x-1]^5 ) , σ>
—》 < [y:=1]^2 ; while [x>1]^3 do ([y:=x*y]^4 ; [x:=x-1]^5 ) , σ’>
—》< while [x>1]^3 do ([y:=x*y]^4 ; [x:=x-1]^5 ) , σ‘’>
—》 < [y:=x*y]^4 ; [x:=x-1]^5 while [x>1]^3 do ([y:=x*y]^4 ; [x:=x-1]^5 ) , σ‘’>
—》< [x:=x-1]^5 while [x>1]^3 do ([y:=x*y]^4 ; [x:=x-1]^5 ) , σ‘’’>
—》 < while [x>1]^3 do ([y:=x*y]^4 ; [x:=x-1]^5 ) , σ‘’‘‘>
—》 σ’‘’‘’
再运用之前所学到的流,将这一完整结构代码细化:
<S, σ> —> σ’ 用流的知识可以表示为 final(S) = {init(S)}
<S, σ> —> <S’,σ’> final (S) 被包含于 final(S’)
flow(S) 被包含于 flow(S’)
blocks(S) 被包含于 blocks(S’)
此时我们是否可以用结构归纳法对上述描述进行归纳
活变量正确性证明 Correctness of Live Variable Analysis
证明活变量是正确的只需要证明确实只有活变量才对我们程序运行结果产生影响。
我们从特殊到一般,首先用x=y+z来考虑:
我们令V1={y,z} V2={x},同时用~表示相等关系:σ1 ~v1 σ2 ( σ1(y,z) = σ2(y,z) )
显然,当σ1 ~v1 σ2 时σ1 ~v2 σ2也成立。也就是说 ~ 的关系不会因为计算而改变。因此我们将计算前和计算后状态分开,分别用N,X表示。N(l) = live entry (l) X(l) = live exit (l)
同时,由于~不会改变,只要在一段代码执行中活变量依旧是活变量,结果就不会改变,用符号表示就是:σ1 ~X(l) σ2 —> σ1 ~N(l’) σ2 所以只有活变量才会对程序运行结果有影响。也就是说:<S,σ1> —> <s’,σ1′> σ1 ~N(init(S)) σ2就会有σ2’满足<S,σ2> —> <s’,σ2′> σ1‘ ~N(init(S‘)) σ2’
<S,σ1> —> σ1’ σ1 ~N(init(S)) σ2就会有σ2’满足<S,σ2> —> σ2’ σ1‘ ~X(l) σ2’
我们回过头来看之前讲的可用表达式分析,必定使用表达式分析,结果表达式分析,活变量分析来寻找其中共性搭建一个框架。
可用表达式分析,我们当时做出了以下结论
AE entry (1) = 空
AE exit (1) = gen AE (x:=a+b) ∪ AE entry (1) = gen AE (x:=a+b)
AE entry (2) = AE exit (1) = gen AE (x:=a+b)
AE exit (2) = gen AE (y:=a*b) ∪ gen AE (x:=a+b)
AE entry (3) = AE exit (2) ∩ AE exit (5) = gen AE (y:=a*b) ∪ gen AE (x:=a+b) ∩ AE exit (5)
AE exit (3) = AE entry (3) = gen AE (y:=a*b) ∪ gen AE (x:=a+b) ∩ AE exit (5)
AE entry (4) = AE exit (3) = gen AE (y:=a*b) ∪ gen AE (x:=a+b) ∩ AE exit (5)
AE exit(4) = AE entry (4) \ kill AE (a+b , a*b , a+1) = AE exit (5) \ kill AE (a+b , a*b , a+1)
AE entry (5) = AE exit (4) = AE exit (5) \ kill AE (a+b , a*b , a+1)
AE exit (5) = gen AE (x:=a+b) ∪ AE entry (5) = gen AE (x:=a+b) ∪ AE exit (5) \ kill AE (a+b , a*b , a+1)
我们可以看到 AE entry (3) 是交集,也就是说半序集的逻辑关系是交集,每一次循环的结果都是上一次循环的子集,属于被包含关系,下限是所有表达式的解,上限是空
结果表达式分析
RD entry (1) = { (x,?) , (y,?) }
RD eixt (1) = RD entry (1) \ kill RD { (x,?) , (x,1) (x,5) } ∪ gen RD (x,1)
RD entry (2) = RD exit (1)
RD eixt (2) = RD entry (2) \ kill RD { (y,?) , (y,2) (y,4) } ∪ gen RD { (y,2) }
RD entry (3) = RD exit (2) ∪ RD exit (5)
RD eixt (3) = RD entry (3)
RD entry (4) = RD exit (3)
RD eixt (4) = RD entry (4) \ kill RD { (y,?) , (y,2) (y,4) } ∪ gen RD { (y,4) }
RD entry (5) = RD exit (4)
RD eixt (5) = RD entry (5) \ kill RD { (x,?) , (x,1) (x,5) } ∪ gen RD { (x,5) }
现在我们对所有表达式进行计算从而得出最终结果
RD entry (1) = { (x,?) , (y,?) }
RD eixt (1) = { (x,1),(y,?) }
RD entry (2) = { (x,1),(y,?) }
RD eixt (2) = { (x,1),(y,2)}
RD entry (3) = { (x,1),(y,2) }
RD eixt (3) = { (x,1),(y,2) }
RD entry (4) = { (x,1),(y,2) }
RD eixt (4) = { (x,1),(y,4) }
RD entry (5) = { (x,1),(y,4) }
RD eixt (5) = { (x,5),(y,4) }
RD entry (3) = { (x,5),(y,4) }
RD eixt (3) = { (x,5),(y,4) }
RD entry (4) = { (x,5),(y,4) }
RD eixt (4) = { (x,5),(y,4) }
RD entry (5) = { (x,5),(y,4) }
RD eixt (5) = { (x,5),(y,4) }
我们可以看到运行过程中,每一句改变x,y的代码都发挥了作用。最后的结果是经过共同处理的结果。也就是说,半序集的逻辑关系是并集,每一次循环的结果都包含于下一次循环,下限是空,上限是所有表达式的结果
必定使用表达式分析
VB exit (1) = VB entry (2) ∩ VB entry (4)
VB exit (2) = VB entry (3)
VB exit (3) = 空
VB exit (4) = VB entry (5)
VB exit (5) = 空
VB entry (1) = VB exit (1) = {a-b} ∪ {b-a} ∩ {a-b} ∪ {b-a}
VB entry (2) = VB exit (2) ∪ {b-a} = {a-b} ∪ {b-a}
VB entry (3) = VB exit (3) ∪ {a-b} = {a-b}
VB entry (4) = VB exit (4) ∪ {b-a} = {a-b} ∪ {b-a}
VB entry (5) = VB exit (5) ∪ {a-b} = {a-b}
这里,我们使用了逆流分析,init(S) 是 VB exit(5) final(S) = VB entry (1)
我们可以看到结果是交集,也就是说半序集逻辑关系是交集,属于被包含关系。下限是所有表达式结果。
活变量表达式
我们选择逆流分析
LV entry (1) = LV exit (1) \ kill LV (x:=2)
LV exit (1) = LV entry (2)
LV entry (2) = LV exit (2) \ kill LV (y:=4)
LV exit (2) = LV entry (3)
LV entry (3) = LV exit (3) \ kill LV (x:=1)
LV exit (3) = LV entry (4)
LV entry (4) = LV exit (4)
LV exit (4) = LV entry (5) ∪ LV entry (6)
LV entry (5) = LV exit (5) \ kill LV (z:=y)
LV exit (5) = LV entry (7)
LV entry (6) = LV exit (4) \ kill LV (z:=y*y)
LV exit (6) = LV entry (7)
LV entry (7) = LV exit (7) \kill LV (x:=z)
LV exit (7) = 空
LV entry (7) = {z}
LV entry (6) = {y}
LV entry (5) = {y}
LV entry (4) = {y} ∪{x,y}
LV entry (3) = {y}
LV entry (2) = 空
LV entry (1) = 空
LV exit (7) = 空
LV exit (6) = {z}
LV exit (5) = {z}
LV exit (4) = {y}
LV exit (3) = {y} ∪{x,y}
LV exit (2) = {y}
LV exit (1) = 空
我们可以看到在没有求最终结果的 LV exit(4) 是并集关系,也就是说半序集逻辑关系是并集,属于包含关系。下限是空。
这四种分析方法所建立的模型都是单调的,或单调递增或单调递减,也就是说我们要构建的框架是单调的
建立框架后,我们需要找到通过框架研究问题的方法。对于单调函数并且每一次函数的因变量都是下一次函数的自变量,我们可以选择迭代的方法寻找问题的解。
流程为:初始化流以及标签等需要使用到的数组集合或者表格。每执行一句代码对这些数据进行更新,最后输出结果。
用可用表达式分析的例子来演示
对于这一段代码,它的流是{(2,3),(3,4),(4,5),(5,3)},使用到的表达式是a+b,ab,a+1。我们用U来表示这三个表达式的集合{(a+b),(a\b),(a+1)}
迭代必须有出口,我们先证明结果存在:从理论上,假设有b行代码,有b^2个元素且是满射关系。每一次迭代的最后结果只可能是改变一个变量或者是增加b个变量。对于一个有限的集合,当每一次都增加b个变量时,最后一定会因为达到满集而终止。也就是之前提到的RD = f (RD)。
从上面的例子出发,不断迭代会发现a+b的极限只能是y,也就是x=y=a+b所以确实存在出口,就像使用迭代方法计算阶乘,最后一次循环1的阶乘是1.
接下来验证结果的正确性,也就是正确结果确实存在于集合中:首先,每一次进入这一段代码的数据集合总是包含于所有进入这一段代码可能的数据集合。每一次代码操作可能去除或者新增数据。对于去除的操作,每一次的结果都包含于原先的集合。对于新增,我们可以把新的数据集合表示为原数据集合并上这一次对应函数关系所对应的结果,他一定是包含于所有可能的集合并上上一次所有可能的集合对应同样的函数关系得到的结果。无论如何,不会有大于包含所有可能性集合的集合。也就是说,所有可能的结果都在分析的结果中。
除了迭代法以外,还有一种方式可以计算结果,那就是遍历法,把所有路径全部走一遍。这一方法的结果必定是全部结果并且没有不可能的结果。如同我们在可计算的验证之中提到的,迭代法的结果是近似值,而遍历法不会是近似值,因为如果程序最终崩溃无法得到结果,这一路径就是错误路径,也就不属于结果中的一员。遍历法会在后面的过程间分析使用到。
作者:DR@03@星盟