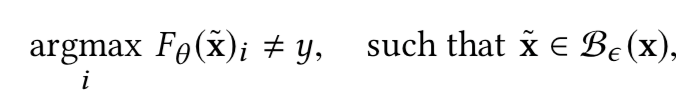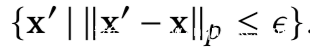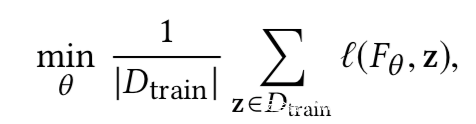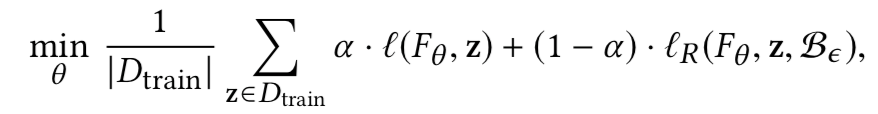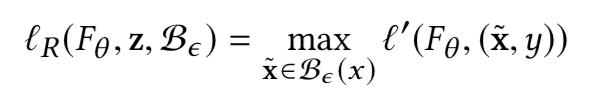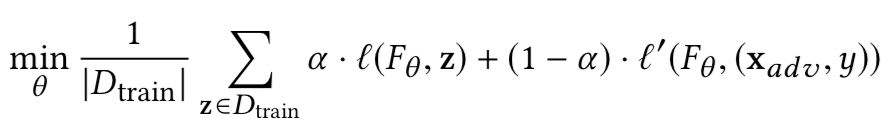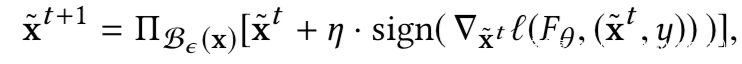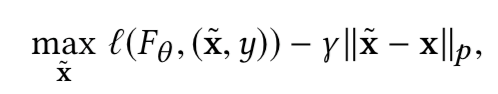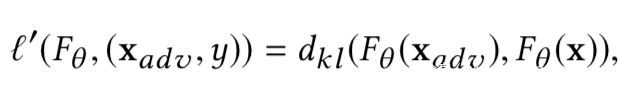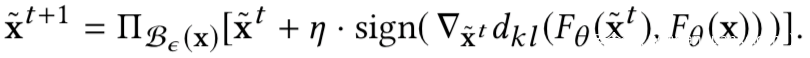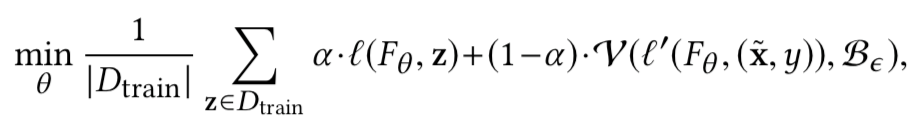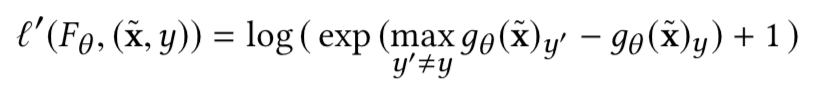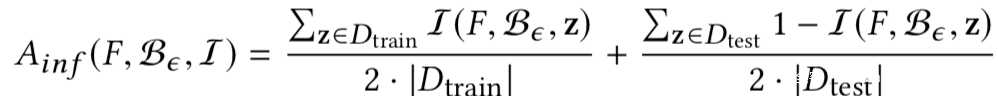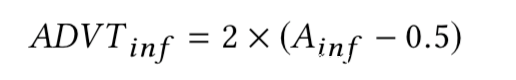前言
银弹(英语:silver bullet)是一种由白银制成的子弹,有时也被称为银弹。在西方的宗教信仰和传说中作为一种武器,是唯一能和狼人、女巫及其他怪物对抗的利器。银色子弹也可用于比喻强而有力、一劳永逸地适应各种场合的解决方案。
计算机科班出身的同学在学习软件工程时,应该都看过或者听说过一本书:《人月神话》,这是软件工程领域的圣经,其中一篇收录的一篇论文名为《没有银弹:软件工程的本质性与附属性工作》,Brooks在其中引用了这个典故 ,说明在软件开发过程里是没有万能的终杀性武器的,只有各种方法综合运用,才是解决之道。而各种声称如何如何神奇的理论或方法,都不是能杀死“软件危机”这头狼人的银弹。此后,在软件界,银弹(Silver Bullet)成了一个通用的比拟流行开来。
在信息安全领域同样如此,也不存在银弹,没有万能、适用于各场景的技术。在工业界做安全永远是在追求trade-off,因为安全、效率和成本三者不可兼得;在学术界则需要兼顾安全和隐私两方面,如果一项技术没有全面经过全面考量,则可能带来更大的潜在风险。
个人的研究方向为人工智能安全,所以本文以人工智能安全领域为例,以实际技术展现“没有银弹”这一真香定律是如何被印证的。
鲁棒性与隐私性
目前人工智能领域的研究存在明显的局限,即安全Security与隐私Privacy通常是分开考虑的,并没有综合考虑两类技术之间的相互影响。事实上,安全与隐私是密不可分的,我们知道在安全领域有四大顶会、两大订刊,其中有S&P,对应的就是Security and Privacy;TIFS,这里的F代表的是Forensics,指的就是隐私,S代表是Security。
我们可以来研究为了提升面临对抗攻击而采取的防御措施,会对隐私保护方面造成什么影响。
在信息安全四大之一的CCS 2019上就有研究人员对六种先进的对抗防御方法保护的模型进行隐私攻击,分析鲁棒模型面临隐私成员推理攻击时的被成功攻击的情况。
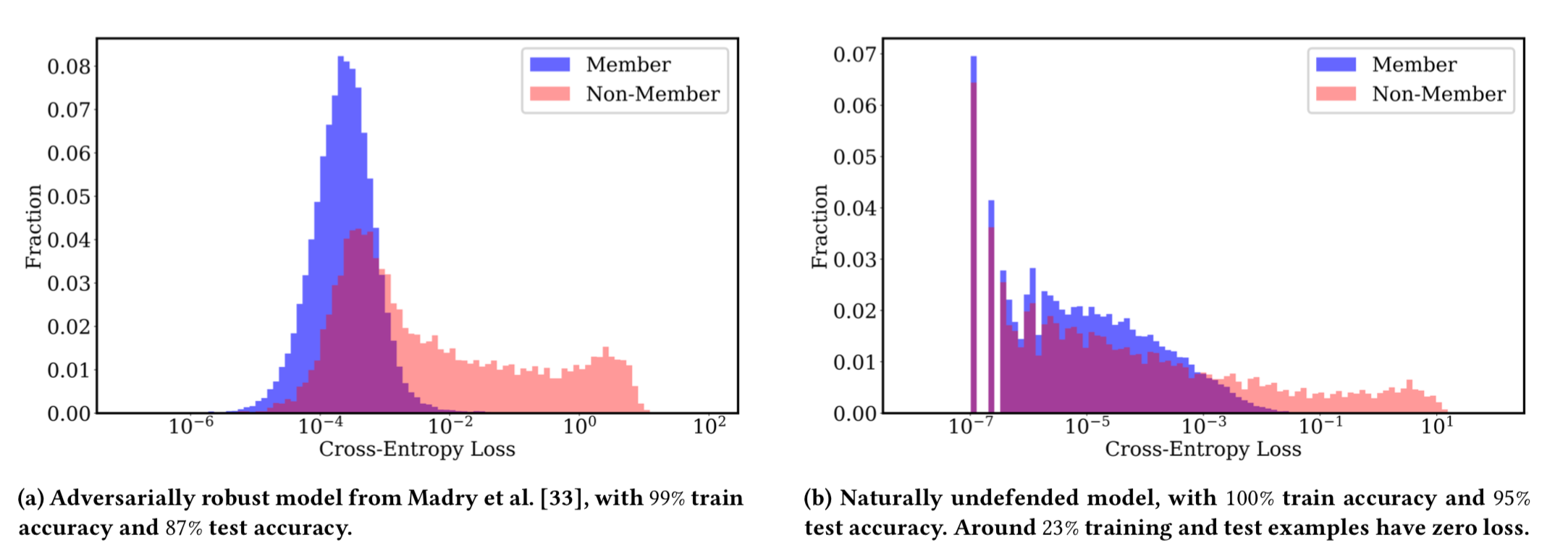
为什么会想到研究这方面的交叉影响呢?我们来看下面这幅图
图中显示的在CIFAR10数据集上训练的自然模型(即没有经过对抗训练等方式防御的原模型)和鲁棒模型(即经过对抗训练等方式极大提升了对抗鲁棒性的模型)的损失值的直方图。这里蓝色的是训练集数据,或者说是成员数据,粉色的测试集数据,或者说是非成员数据。与自然模型相比,我们可以看到,鲁棒模型中成员数据与非成员数据之间的损失分布差异更大,也就是说在鲁棒模型上更容易区分出数据是否为成员数据。
研究人员引入了六种增强对抗鲁棒性的方法以及使用成员推理攻击来评估模型隐私容易被攻击的程度。
增强对抗鲁棒性的六种方案
首先需要定义对抗样本
上式中的B是perturbation budget,也叫做perturbation constraint,扰动约束。一般我们使用lp范数来表示,即B的输出满足
模型正常训练的损失函数为:
但是为了在扰动约束下提供对抗鲁棒性,防御方案都会在此基础上加上额外的鲁棒损失函数,此时整体的损失如下
其中的α是在自然损失与鲁棒损失之间的权衡系数。上式中的lr表示定义为:
上式中的l’可以和l相同,也可以是近似l的损失函数
但是上式的精确解通常很难求解,于是对抗防御方案提出了不同的方式来近似鲁棒损失,我们可以将他们分为两类
Empirical defenses
基于经验的防御方案用先进的攻击方案在每个训练步骤生成对抗样本并计算其预测损失来近似鲁棒损失,此时的鲁棒训练算法可以表示为:
该类方案中我们使用下面三种
PGD-Based Adversarial
使用投影梯度下降方案生生成对抗样本,以最大化交叉熵损失(l’=l),并只在这些对抗样本上进行训练(α=0),此时的对抗样本可以表示为:
Distributional Adversarial Training
通过求解交叉熵损失的拉格朗日松弛来生成对抗样本,公式为:
Difference-based Adversarial Training
使用原样本的输出与对抗样本的输出之间的差异(比如可以使用KL散度)作为损失函数l’,并将其余自然交叉熵损失结合
其中的对抗样本也是使用PGD生成的
只不过现在攻击的目标是最大化输出差异
Verifable defenses
该类方案就是在对抗扰动约束B下计算预测损失l’的上界,如果在经过验证的最坏情况下,输入仍然可以被正确预测,那么就意味着在B下对抗样本不会被预测错误。因此,这类方案在训练期间加入验证过程,使用已验证的最坏情况的预测损失作为鲁棒损失lr,此时的鲁棒训练算法可以如下所示
上式中的V是经过验证的预测损失l’的上界
我们考虑该类类型中的三种典型方案
Duality-Based Verification
通过在非凸ReLU运算上求解其具有凸松弛的对偶问题来计算已验证的最坏损失,然后仅最小化该过度逼近的鲁棒损失值(α = 0,l′= l),此外,通过进一步将这种对偶松弛方法与随机投影技术相结合,可以扩展到更复杂的神经网络结构如ResNet等。
Abstract Interpretation-Based Verification
使用一个抽象域(如区间域)来表示输入层的对抗性扰动约束,并通过对其应用抽象变换,获得模型输出的最大验证范围。他们在logits上采用softplus函数来计算鲁棒损失值,然后将其与自然训练损失(α=0)相结合,即
Interval Bound Propagation-Based Verification
将扰动约束表示为有界区间域,并将该边界传播到输出层。将已验证过的最坏情况输出的交叉熵损失作为鲁棒损失(l′= l),然后与自然预测损失(α 不等于0)结合作为训练期间的最终损失值
成员推理攻击
Shokri等人设计了一种基于训练推理模型的成员推理攻击方法,以区分对训练集成员和非成员的预测。为了训练推理模型,他们引入了影子训练技术:(1)对手首先训练多个模拟目标模型行为的“影子模型”,(2)基于影子模型在自己的训练和测试样本上的输出,对手获得一个标记过的(标签为in表示成员,out表示非成员)数据集,以及(3)最后将推理模型训练为一个神经网络,对目标模型进行推理攻击。推理模型的输入是目标数据记录上的目标模型的预测向量。
原因
成员推理攻击与两个因素有关:
泛化误差
成员推断攻击的性能与目标模型的泛化误差高度相关。一些非常简单的攻击方案可以根据输入是否被正确分类来进行成员推理攻击,此时,目标模型的训练和测试精度之间的巨大差异导致了极大的成员推断攻击成功率(因为大多数成员数据会被被正确分类,而非成员数据不会)。而又有研究表明,鲁棒训练会导致模型在测试阶段的准确率下降,当使用对抗样本评估模型的鲁棒模型的准确率时,泛化误差会更大。
所以,与自然模型相比,鲁棒模型会泄露更多的成员数据信息。
模型敏感度
成员推断攻击的性能与目标模型对训练数据的敏感性相关。敏感性是指一个数据点对目标模型的性能的影响,它是通过计算在有和没有这个数据点的情况下模型训练的预测差来实现的。直观上来说,当数据点对模型的影响较大,即模型对该数据较敏感时,模型对应的预测是不同于对其他数据点的预测是,因此攻击者可以很容易地区分是否为成员数据。而防御方案,或者说鲁棒训练算法,为了提升鲁棒性,其为确保训练数据点周围的小区域,模型对其的预测保持相同,从而放大了训练数据对模型的影响。
所以,与自然模型相比,防御方案增加了鲁棒模型对训练数据的敏感性,泄露了更多的成员数据信息,模型更容易受到成员推理攻击。
成员推理攻击度量
我们使用下式评估成员推理攻击的准确性:
上式中的I函数,如果是成员数据则为1,否则为0
随机猜测的话,很明确,准确性是50%,为了进一步衡量成员推理攻击的有效性,可以使用成员推理优势来定义,其定义为:
实验分析
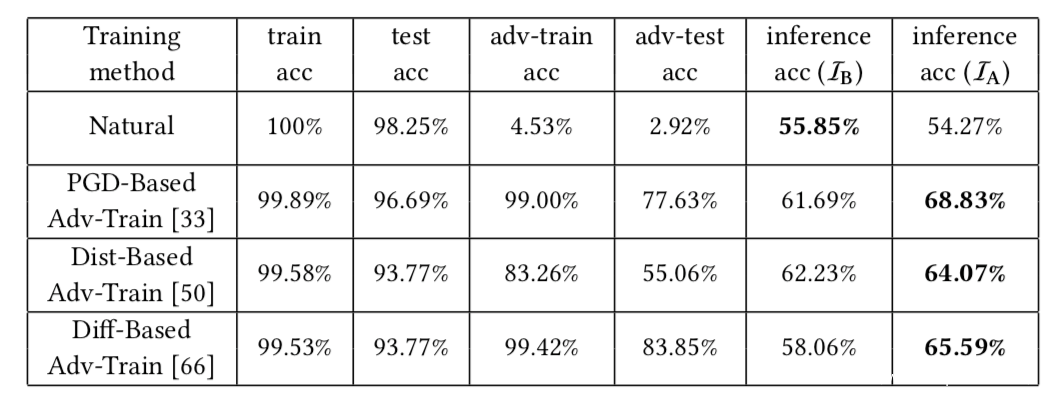
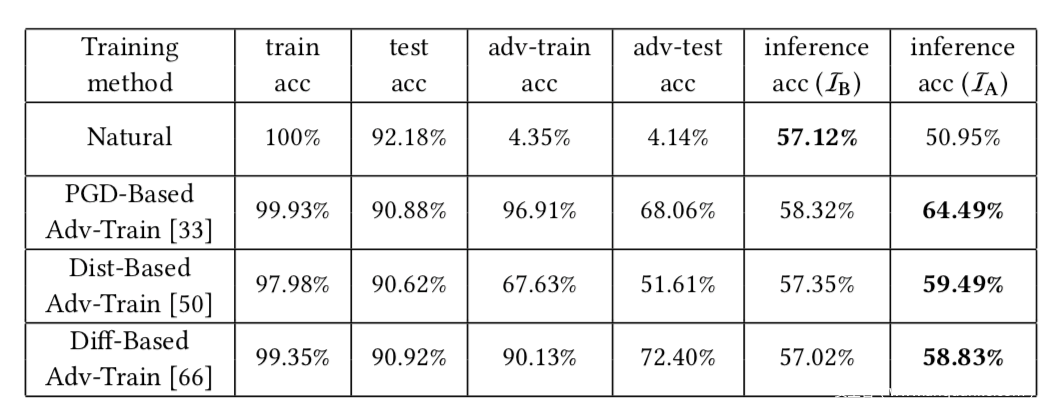
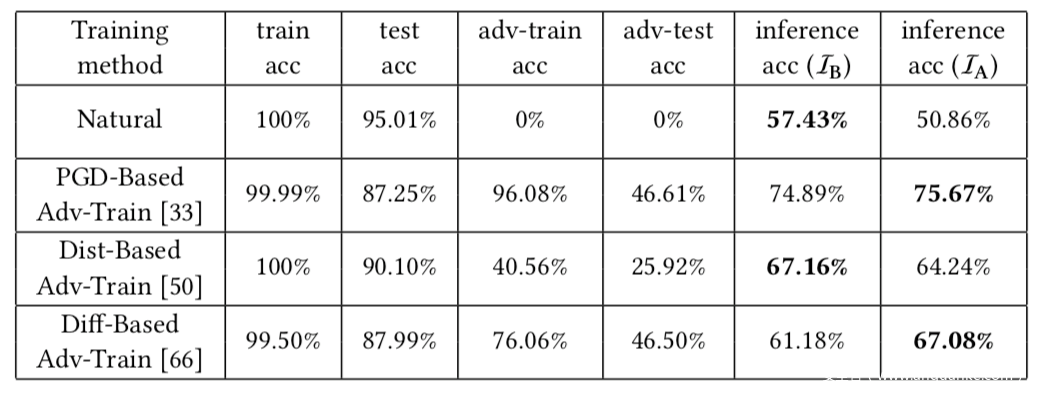
表中的acc表示accuracy,而adv-train acc,adv-test acc表示在PGD攻击上的accuracy,从结果可以看到,这三类empirical defense方法在使模型更鲁棒的同时,也会让模型更容易受到隐私攻击
上表是在Yale Face数据集上的实验结果,基于上文中最近给出的那条公式,我们可以算出,自然模型具有11.70%的推理优势,而鲁棒模型具有37.66%的推理优势
上表是在Fashion-MNIST数据集上的实验结果,同样可以计算得到自然模型具有14.24%的推理优势,而鲁棒模型具有高达28.98%的推理优势。
上表是在CIFAR10数据集上的实验结果,同样可以计算得到自然模型具有14.86%的推理优势,而鲁棒模型具有高达51.34%的推理优势.
我们还可以更仔细地进行分析敏感性和泛化误差,这里以CIFAR10数据集为例,分析使用基于PGD的对抗训练方法对成员推理攻击的影响。
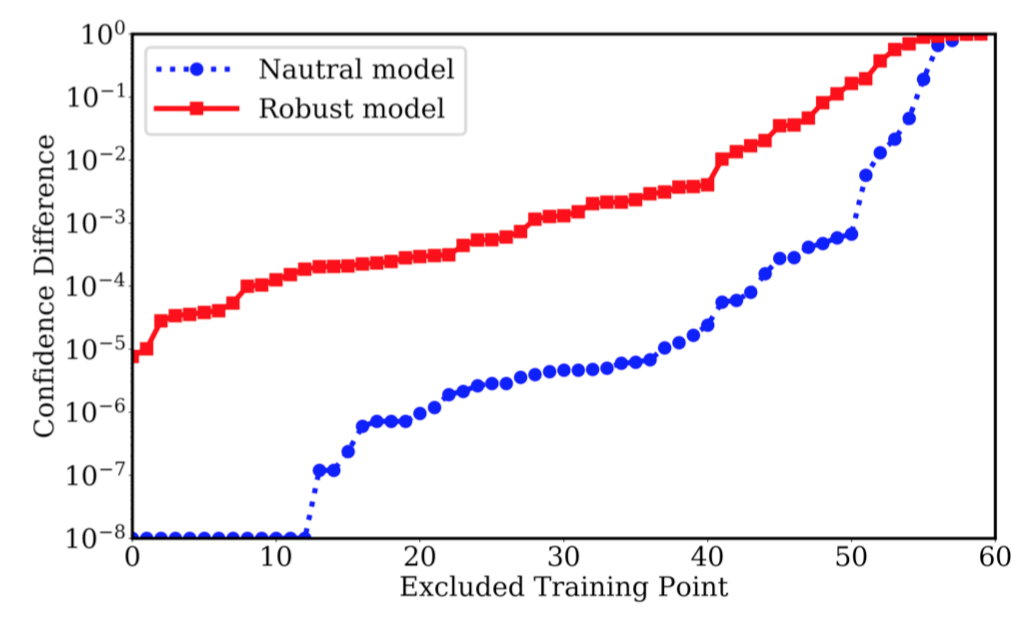
下表是对两个模型做了敏感性分析,图中x轴是重训练过程中不在训练集中的的数据点的id编号(以敏感性大小排序),y轴则是原模型与重训练模型之间的预测置信度的差异,这是衡量模型灵敏度的。从图中可见,与自然模型相比,鲁棒模型对训练数据更加敏感。
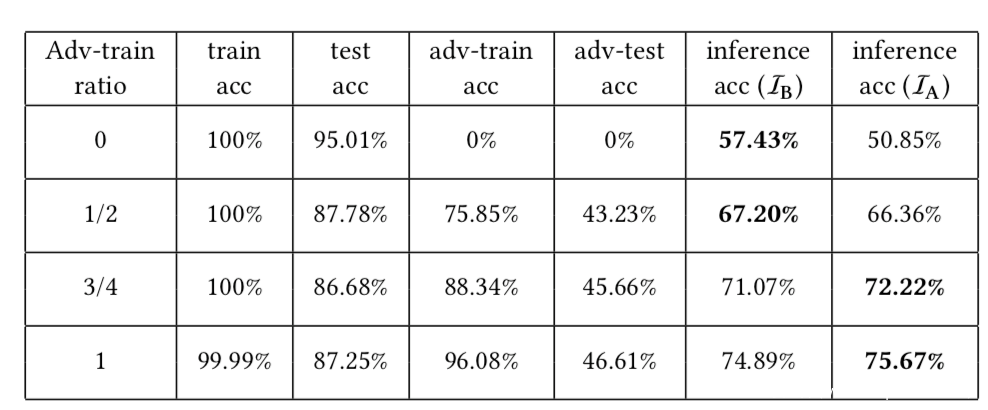
下面则是分析泛化误差的表,从表中可以看到,随着更多的训练点用于计算训练损失,由于在测试精度和训练精度上的泛化误差更加扩大,所以成员推理攻击的精度也增加了。
限于篇幅,另外三种增强模型对抗鲁棒性的方案对于隐私攻击的作用这里不再分析,效果也是类似的。
对抗攻击与后门攻击
上一部分介绍的是安全与隐私两个方面之间的相互影响,那么在安全方面,我们熟悉的对抗攻击和后门攻击又会有什么样的相互影响呢?
在安全四大之一的CCS 2020的论文《A Tale of Evil Twins: Adversarial Inputs versus Poisoned Models》则研究了两者的影响。
这篇文章实际上探索的是攻击方案中的关键组件:对抗攻击中的对抗样本以及后门攻击中的毒化模型,文章研究的是这两个攻击向量之间的相互影响。
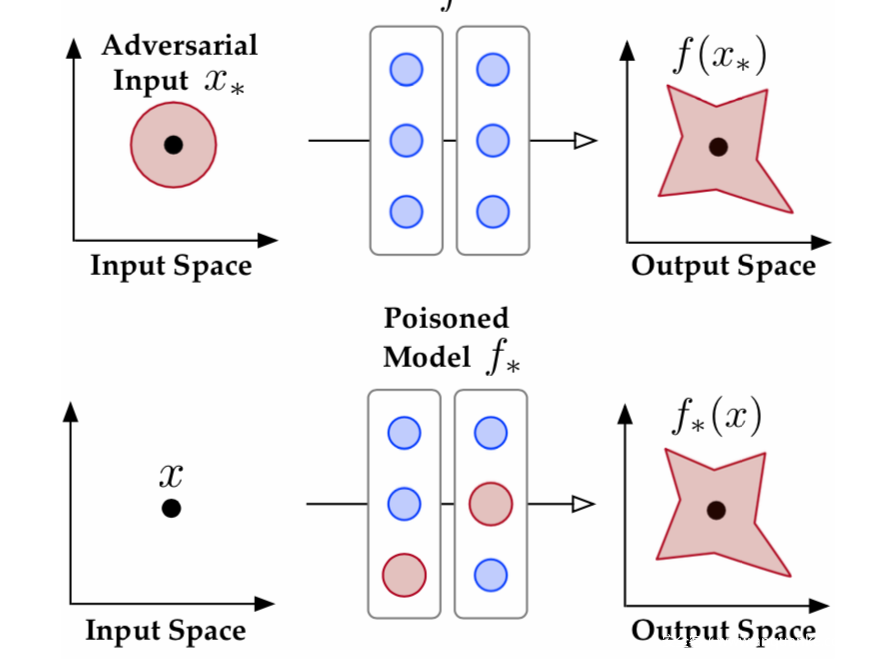
把这两个攻击向量放在一起比较的话,会更直观一点,我们可以看下图:
对抗样本是扰动良性样本x,得到x*,将其输入良性模型f,导致模型分类出错
毒化模型是扰动良性模型f,得到f*,将良性样本x输入f*,导致模型分类出错
攻击目的是一样的,但是手段不同
对抗样本是以fidelity,即保真度为代价对良性样本进行扰动(需要确保对抗样本保留了原样本的感知质量),而毒化模型以sepcificity,即特异性为代价,对良性模型进行扰动(需要确保不会影响到非目标类别样本的预测)。
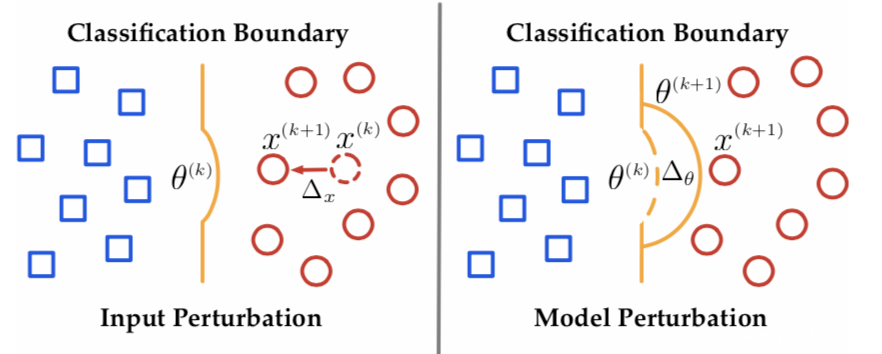
两类扰动可以用下图形象表示出来
研究人员将两类攻击向量纳入统一的框架进行综合实验,发现了有意思的结论如下
杠杆效应
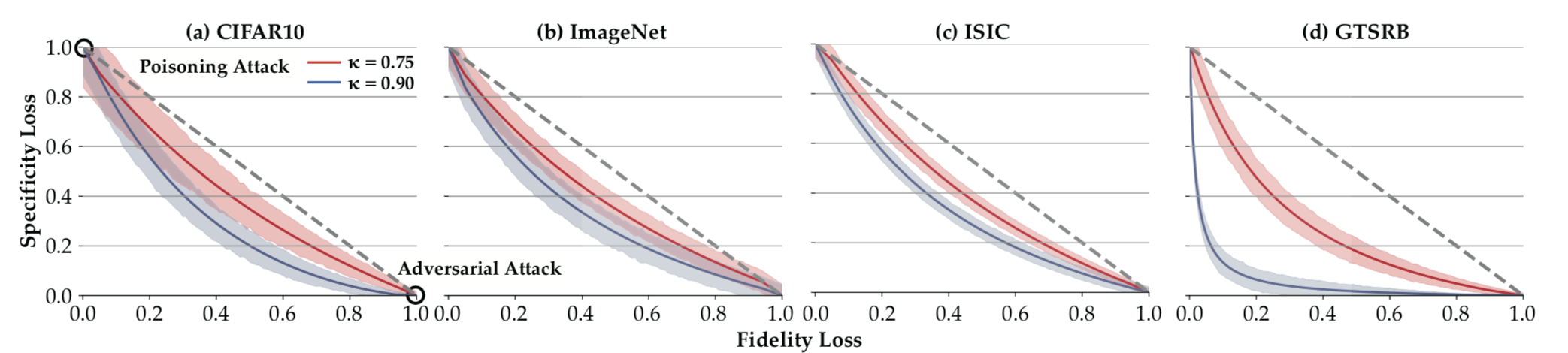
下表所示是在四个数据集上的实验,研究的是在统一攻击时,如何在对抗样本的保真度和毒化模型的特异性之间进行权衡
从表中我们可以看到,在攻击效率(k)一定的情况下,两者之间存杠杆效应,以图d为例,当保真度损失从0增加到0.05,特异性损失减少了0.48以上;而特异性损失的轻微增加也会导致保真度的显著提高,如图a,随着特异性损失从0增加到0.1,特异性损失下降0.37。
该效应的发现告诉我们,攻击者在设计攻击方案时需要考虑更多的因素,才能实现完美的攻击。
强化效应
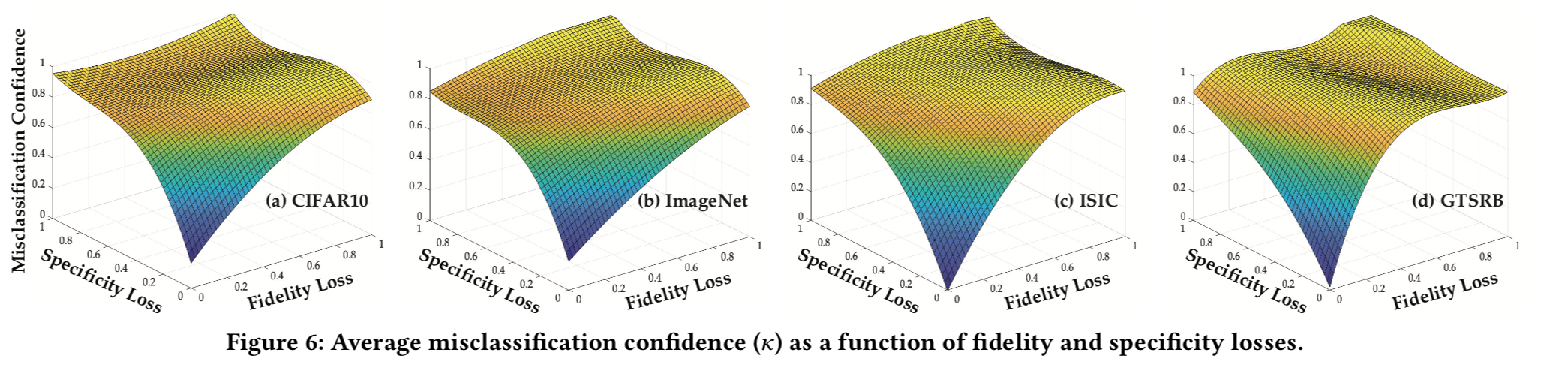
研究人员测量了不同的保真度和特异性损失下,对抗攻击、中毒攻击以及联合攻击可以到的攻击效果(用平均错误分类置信度表示),如下图所示
首先我们发现,联合攻击比单个的攻击实现了更强的攻击效果,例如在ISIC的情况下(图 (c)),保真度损失固定为0.2,敌对攻击达到约0.25;特异性损失固定为0.2,中毒发作达到为0.4左右;而在这种设置下,IMC达到0.8以上的,这是因为联合攻击时同时优化了训练和推理过程中引入的扰动;其次我们发现,联合攻击可以到达单个攻击无法达到的攻击效能。在四个图中,联合攻击在适当的保真度和特异性下可以达到 = 1,而单独的对抗(或后门)攻击(即使保真度或特异性损失固定为1)仅能够到达小于0.9的。
这一效应的发现告诉我们攻击者在设计攻击方案时,如果希望实现更强的攻击效果,可以考虑同时引入这两类技术,甚至可以起到1+1>2的效果。
对抗防御与后门防御
在安全的防御方面,我们熟悉的对抗攻击和后门攻击又会有什么样的相互影响呢?
来自NeurIPS 2020的论文研究了对抗鲁棒性对后门鲁棒性之间的影响。
用于提升对抗鲁棒性的防御技术已经介绍过了,我们这里不再赘述。
原因
为什么通过防御方案提升了对抗鲁棒性的模型更容易受到后门攻击呢?我们可以用可视化技术来进行分析
上图中给出了大象图像的原图与毒化图像(右下角加了火狐浏览器的logo作为触发器)的salience map(模型预测相对于输入的梯度),图b是原模型给出的显著图,图c是鲁棒模型给出的显著图,很明显,在c中我们可以看到,经过对抗训练的鲁棒模型更依赖于高级特征做出预测,这些特征更符合人类的感知,所以它倾向于从触发器中进行学习,因为触发器提供了与目标标签密切相关的鲁棒特征,所以在c中的右边的图中可以看到,模型更加关注触发器所在的位置。
实验分析
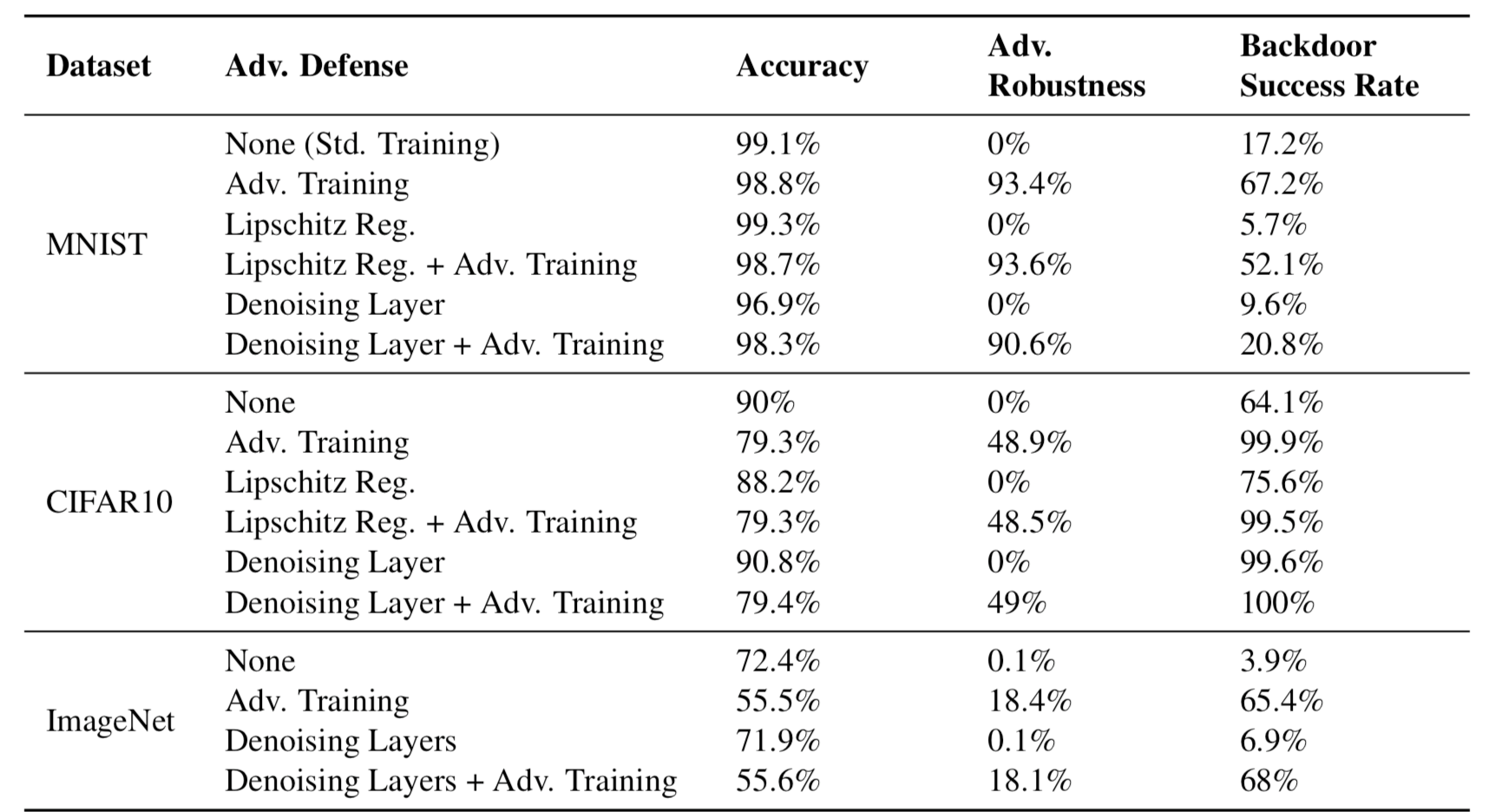
下表给出的是各种增强对抗鲁棒性的方案接受评估时的测量得到的指标,我们主要关注第4,5列,可以看到。第一行是原模型,其他的都是鲁棒模型,可以看到,鲁棒模型的鲁棒性确实相比原模型上升了,但是相应地,后门攻击成功率也上升了
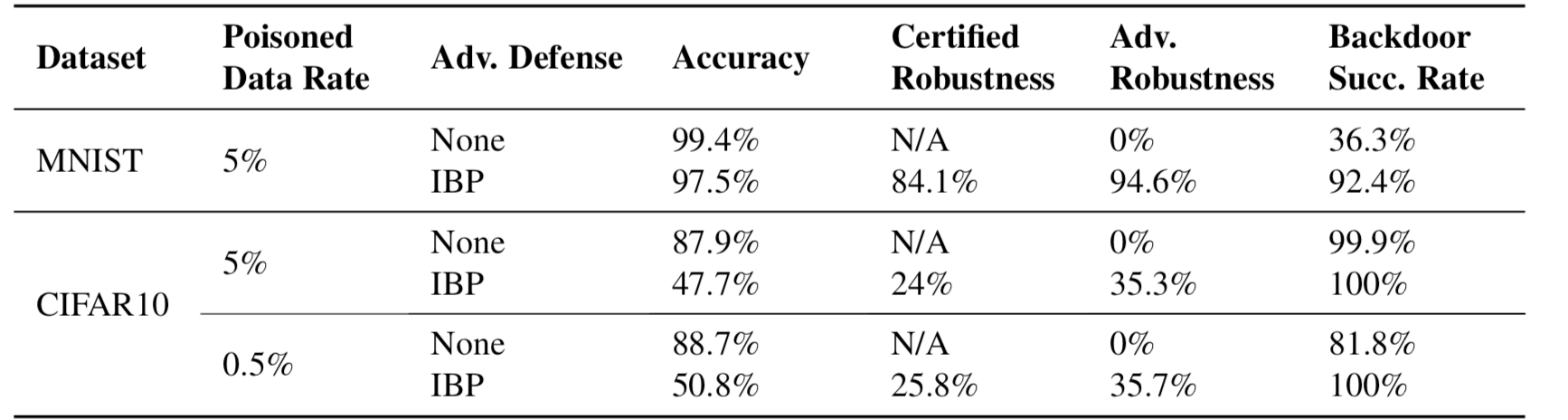
上表给出的是empirical defense的总结结果,下表给出的是certified robustness方案的总结结果
从结果中我们也可以得出同样的结论
总结
安全领域没有银弹,总是需要在各类因素之间做出权衡。
出现对抗攻击后,研究人员想尽办法提升对抗鲁棒性,但是却没有考虑到鲁棒性的提升也加剧了隐私保护方面的风险,安全与隐私兼顾并不容易。除了安全与隐私两方面见的交叉影响外,安全方面的攻击方案之间也存在相互影响,对抗攻击和后门攻击便是如此,在攻击方面,两类方案会相互影响,不仅存在杠杆效应,还存在相互强化的效应,这就给安全防御带来了挑战,利用杠杆效应,攻击者只需要在承受较小的一方面的损失,确保回去较大的另一方面的回报;而利用强化效应,更是可以实现单一攻击向量不具备的攻击效果。而在防御方面,对抗鲁棒性好的模型更容易受到后门攻击,这意味着面临攻击时,我们采取的防御方案看似保证了安全,但实际上引入了另一类攻击的风险,这反而会给我们造成假象,迷惑我们。
安全领域没有银弹,所以才有红蓝双方的arms race,攻防技术才能不断发展,这正是我们安全从业人员的兴趣所在。
参考
1.https://zh.wikipedia.org/wiki/%E9%8A%80%E8%89%B2%E5%AD%90%E5%BD%88
2.https://baike.baidu.com/item/%E6%B2%A1%E6%9C%89%E9%93%B6%E5%BC%B9/5036116
3.Privacy Risks of Securing Machine Learning Models against Adversarial Examples
4.A Tale of Evil Twins: Adversarial Inputs versus Poisoned Models
5.On the Trade-off between Adversarial and Backdoor Robustness