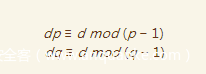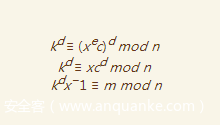前言
2018-noxCTF的密码题中有许多RSA的题目，正好最近在看RSA，于是就做了一下，难度并不是很大
Chop Suey
题目如下
Today I ate in a Chinese restaurant and got myself a fortune cookie. These things usually contain a note with a nice sentence or phrase, but mine had numbers in it instead! Can you help me find the meaning of the numbers?
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
题目分析
还是先摆出已知条件
我们的目标很简单，如何从这些式子得到答案
首先根据
因为
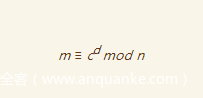
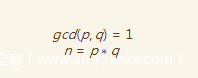
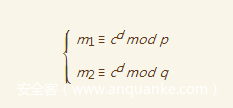
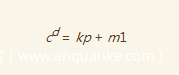
利用中国剩余定理,我们可以得到
由式1可以得到
我们把这个带入式2
可以得到
等式两边同时减去m1,可以得到
这里因为
所以可以求p的逆元，得到
所以这里得到如下两个式子
我们上下两个式子合并，得到
最后可以有
那么问题来了
这里的m1和m2怎么求？
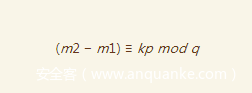
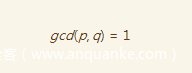
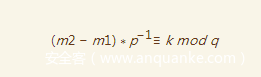
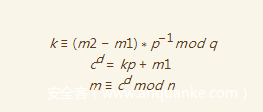
这时候我们有
那么分别带入，有
所以我们有
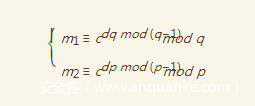
Payload
推导完成后，写脚本即可
from Crypto.Util import number
import gmpy2
import libnum
def decrypt(dp,dq,p,q,c):
InvQ = gmpy2.invert(q, p)
mp = pow(c, dp, p)
mq = pow(c, dq, q)
m = (((mp-mq)*InvQ) % p)*q+mq
print libnum.n2s(m)
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
decrypt(dp,dq,p,q,c)
得到结果
noxCTF{W31c0m3_70_Ch1n470wn}
Decryptor
题目如下
I created this nice decryptor for RSA ciphertexts, you should try it out!
nc chal.noxale.com 4242
Oh, and someone told me to give this to you:
N = 140165355674296399459239442258630641339281917770736077969396713192714338090714726890918178888723629353043167144351074222216025145349467583141291274172356560132771690830020353668100494447956043734613525952945037667879068512918232837185005693504551982611886445611514773529698595162274883360353962852882911457919
c = 86445915530920147553767348020686132564453377048106098831426077547738998373682256014690928256854752252580894971618956714013602556152722531577337080534714463052378206442086672725486411296963581166836329721403101091377505869510101752378162287172126836920825099014089297075416142603776647872962582390687281063434
e = 65537
题目分析
我们nc过去后，得到提示
Please insert your ciphertext to decrypt in hex form:
所以看来服务器是会解密我们input的密文
那么这里就是一个典型的选择密文攻击，我们现在有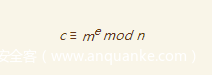
我们可以构造一个x，使得
然后我们把k发送过去，得到
Payload
所以这里就很简单了，我们构造x=2即可
即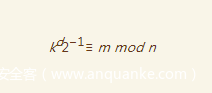
所以我们Input k
hex((pow(2,e,N)*c)%N)[2:-1]
得到解密结果：
dcdef086a88cf660ea6ee6da68e46e66c8fa
我们解密即可得到flag
tmp = 0xdcdef086a88cf660ea6ee6da68e46e66c8fa
print libnum.n2s((tmp*gmpy2.invert(2,N))%N)
得到noxCTF{0u7sm4r73d}
WTF
题目如下
Um uhhhhhhhhh WTF IS THIS?! I give up. Now you try to solve this.
N = lObAbAbSBlZOOEBllOEbblTlOAbOlTSBATZBbOSAEZTZEAlSOggTggbTlEgBOgSllEEOEZZOSSAOlBlAgBBBBbbOOSSTOTEOllbZgElgbZSZbbSTTOEBZZSBBEEBTgESEgAAAlAOAEbTZBZZlOZSOgBAOBgOAZEZbOBZbETEOSBZSSElSSZlbBSgbTBOTBSBBSOZOAEBEBZEZASbOgZBblbblTSbBTObAElTSTOlSTlATESEEbSTBOlBlZOlAOETAZAgTBTSAEbETZOlElBEESObbTOOlgAZbbOTBOBEgAOBAbZBObBTg
e = lBlbSbTASTTSZTEASTTEBOOAEbEbOOOSBAgABTbZgSBAZAbBlBBEAZlBlEbSSSETAlSOlAgAOTbETAOTSZAZBSbOlOOZlZTETAOSSSlTZOElOOABSZBbZTSAZSlASTZlBBEbEbOEbSTAZAZgAgTlOTSEBEAlObEbbgZBlgOEBTBbbSZAZBBSSZBOTlTEAgBBSZETAbBgEBTATgOZBTllOOSSTlSSTOSSZSZAgSZATgbSOEOTgTTOAABSZEZBEAZBOOTTBSgSZTZbOTgZTTElSOATOAlbBZTBlOTgOSlETgTBOglgETbT
c = SOSBOEbgOZTZBEgZAOSTTSObbbbTOObETTbBAlOSBbABggTOBSObZBbbggggZZlbBblgEABlATBESZgASBbOZbASbAAOZSSgbAOZlEgTAlgblBTbBSTAEBgEOEbgSZgSlgBlBSZOObSlgAOSbbOOgEbllAAZgBATgEAZbBEBOAAbZTggbOEZSSBOOBZZbAAlTBgBOglTSSESOTbbSlTAZATEOZbgbgOBZBBBBTBTOSBgEZlOBTBSbgbTlZBbbOBbTSbBASBTlglSEAEgTOSOblAbEgBAbOlbOETAEZblSlEllgTTbbgb
题目分析
拿到题目，乍一看非常奇怪，因为(n,e,c)都是编码过的，我们没有办法直接破解，尝试了一些常见编码方式，都无法破解，于是统计了一下
for i in (N,e,c):
print list(collections.Counter(i))
得到结果
['A', 'B', 'E', 'g', 'l', 'O', 'S', 'b', 'T', 'Z']
['A', 'B', 'E', 'g', 'l', 'O', 'S', 'b', 'T', 'Z']
['A', 'B', 'E', 'g', 'l', 'O', 'S', 'b', 'T', 'Z']
发现都一样，并且长度为10，这里就需要开个脑洞了
将字母象形为0-9
即
dict = {
'O' : '0',
'l' : '1',
'Z' : '2',
'E' : '3',
'A' : '4',
'S' : '5',
'b' : '6',
'T' : '7',
'B' : '8',
'g' : '9'
}
然后写脚本替换
for key,value in dict.items():
N = N.replace(key,value)
c = c.replace(key,value)
e = e.replace(key,value)
n = int(N)
c = int(c)
e = int(e)
发现e极大
18165674577527345773800436360005849487629584246818834218136555374150149407637407524285601002127374055517203100485286275425145721883636036574242949710753834106366928190387866524288552807173498852374689387479028711005571557055252495247965030797704485232834280077859527260792773150470416827810790513797809193767
于是想到winner攻击
payload
使用github的winner attack的脚本
https://github.com/pablocelayes/rsa-wiener-attack
运行
➜ rsa-wiener-attack-master python RSAwienerHacker.py
Hacked!
noxCTF{RSA_1337_10rd}
Trinity
题目如下
Neo, you are the chosen one. The only person who can make sense of these numbers. Do it.
N = 331310324212000030020214312244232222400142410423413104441140203003243002104333214202031202212403400220031202142322434104143104244241214204444443323000244130122022422310201104411044030113302323014101331214303223312402430402404413033243132101010422240133122211400434023222214231402403403200012221023341333340042343122302113410210110221233241303024431330001303404020104442443120130000334110042432010203401440404010003442001223042211442001413004
c = 310020004234033304244200421414413320341301002123030311202340222410301423440312412440240244110200112141140201224032402232131204213012303204422003300004011434102141321223311243242010014140422411342304322201241112402132203101131221223004022003120002110230023341143201404311340311134230140231412201333333142402423134333211302102413111111424430032440123340034044314223400401224111323000242234420441240411021023100222003123214343030122032301042243
N = 302240000040421410144422133334143140011011044322223144412002220243001141141114123223331331304421113021231204322233120121444434210041232214144413244434424302311222143224402302432102242132244032010020113224011121043232143221203424243134044314022212024343100042342002432331144300214212414033414120004344211330224020301223033334324244031204240122301242232011303211220044222411134403012132420311110302442344021122101224411230002203344140143044114
c = 112200203404013430330214124004404423210041321043000303233141423344144222343401042200334033203124030011440014210112103234440312134032123400444344144233020130110134042102220302002413321102022414130443041144240310121020100310104334204234412411424420321211112232031121330310333414423433343322024400121200333330432223421433344122023012440013041401423202210124024431040013414313121123433424113113414422043330422002314144111134142044333404112240344
N = 332200324410041111434222123043121331442103233332422341041340412034230003314420311333101344231212130200312041044324431141033004333110021013020140020011222012300020041342040004002220210223122111314112124333211132230332124022423141214031303144444134403024420111423244424030030003340213032121303213343020401304243330001314023030121034113334404440421242240113103203013341231330004332040302440011324004130324034323430143102401440130242321424020323
c = 10013444120141130322433204124002242224332334011124210012440241402342100410331131441303242011002101323040403311120421304422222200324402244243322422444414043342130111111330022213203030324422101133032212042042243101434342203204121042113212104212423330331134311311114143200011240002111312122234340003403312040401043021433112031334324322123304112340014030132021432101130211241134422413442312013042141212003102211300321404043012124332013240431242
题目分析
看到3组(n,c)，第一反应想到的就是低指数广播攻击,即我们有
根据中国剩余定理，可以有通解
其中
但是由于这里没有给e，又因为低指数，于是我选择爆破了一下e，但是都没有结果
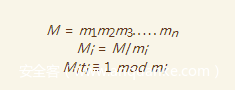
发现一直报错
ZeroDivisionError: invert() no inverse exists
想到题目给的数字可能有问题，仔细观察，发现只有0-4
于是想到5进制
转一波以后就正常了
Payload
import gmpy2
import gmpy
import libnum
def boradcast_fuzz(question,e):
N=1
for i in range(len(question)):
N *= question[i]['n']
N_list = []
for i in range(len(question)):
N_list.append(N / question[i]['n'])
t_list = []
for i in range(len(question)):
t_list.append(int(gmpy2.invert(N_list[i], question[i]['n'])))
sum = 0
for i in range(len(question)):
sum = (sum + question[i]['c'] * t_list[i] * N_list[i]) % N
sum = gmpy.root(sum, e)[0]
return libnum.n2s(sum)
n1 = int(str(n1),5)
n2 = int(str(n2),5)
n3 = int(str(n3),5)
c1 = int(str(c1),5)
c2 = int(str(c2),5)
c3 = int(str(c3),5)
question=[
{'n':n1,'c':c1},
{'n': n2, 'c': c2},
{'n':n3,'c':c3},
]
for i in range(2,20):
res = boradcast_fuzz(question,i)
if 'noxCTF' in res:
print res
print 'e=%d'%(i)
break
得到结果
noxCTF{D4mn_y0u_h4s74d_wh47_4_b100dy_b4s74rd!}
e=3
拓展-Boneh and Durfee attack
由于题目中有一道Wiener’s Attack，于是我联想到了最近看的
Boneh and Durfee attack
我们知道，如果要使用Wiener’s Attack，有一个特征，即e很大，那么到底有多大？
这里有一个评判标准，即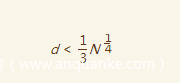
那么如果e很大，但d比这里的限定值大怎么办？
那么可以尝试Boneh and Durfee attack
其使用标准为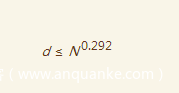
比如这次题目里
d=33859466522204630502415021058361047681307615225229354334148022345758288750359
n=106464658120038110366171046017584728605432723415099799671398095113303220554018149888866005570730116293196252665770382258833879353944414043672822102509840890423260826373058255315521685967807858850204383823245609286166175687064317570157147353365780181201403742497875436372013183350667001942660780839408462806879
我们简单比较下
N1 = 1.0/3*pow(n,1.0/4)
N2 = pow(n,0.292)
print int(N1)-d
print int(N2)-d
得到结果
941571295587957309748289456353490745482373040518812393691369
878909169550944842698019812370775334246473513796204883182700468007058108344282016448403689
明显Boneh and Durfee attack给的空间更大，所以如果我们在不能使用Wiener’s Attack的时候，可以尝试Boneh and Durfee attack
利用脚本
https://github.com/mimoo/RSA-and-LLL-attacks